24. Уравнение в полных дифференциалах.

Уравнение называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции U (x, y) и следовательно его можно записать в виде: dU=0 U=const=С.

Если функции M и N в области задания непрерывны и имеют частные производные соответственно по y и по x, то для того чтобы уравнение было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество , если это условие выполнено, то решение можно записать в виде (1), либо (2) где – произвольная точка в области задания функций M и N.

Частное решение, удовлетворяющее начальным условиям , в случае когда функции M и N не обращаются одновременно в 0 в точке , можно найти обычным путем, определив константу c из общего решения, а можно в формулах (1) и (2) положить , то есть

, либо .

25. Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка.

ДУ порядка выше первого называется ДУ высших порядков.

Общее решение:

Частное решение: при начальных условиях

Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка. Т.е. уравнения вида . Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием:

26. Линейные дифференциальные уравнения. Определитель Вронского. Фундаментальная система решений.

Линейные дифференциальные уравнения высших порядков называется . ЛДУ называется приведенным, если коэффициент при старшой производной равен 1. Правую часть называют свободным членом.

Определитель Вронского.

Если функции и на интервале линейно зависимы, то

Теорема. Если функции и линейно независимые решения ДУ на интервале , то определитель Вронского на этом интервале нигде не обращается в ноль.

Определитель Вронского 2-ч частных решений не равен 0 ни в одной точке , тогда и только тогда когда эти частные решения линейно независимы.

Говорят что совокупность двух линейно независимых на интервале функция и линейного однородного ДУ образуют фундаментальную систему решений

27. Линейные однородные дифференциальные уравнения n-того порядка. Фундаментальная система решений. Определитель Вронского.

Линейные однородные дифференциальные уравнения n-того порядка имеет вид

Если - являются решением, то - также решение.

Определитель Вронского имеет вид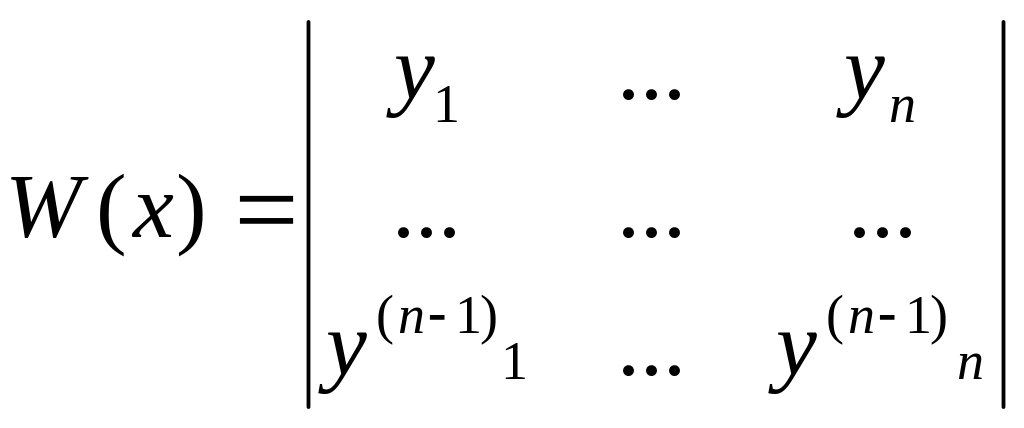

Частные решения уравнения образуют фундаментальную систему решения на если ни в одной точке этого интервала не обращаются в 0.

Определитель Вронского либо тождественно равен 0, это означает что решения - линейно зависимы либо не обращаются в 0, ни в одной точке и это означает, что решения линейно независимы.