42. Условное математическое ожидание. Корреляционный момент и коэффициент корреляции. Свойства коэффициента корреляции.

Условное математическое ожидание дискретной случайной величины Y при называется следующая величина .

Для непрерывных случайных величин - функция регрессии случайной величины y на x.

Для дискретных случайных величин для характеристики связи между ними вводят корреляционный коэффициент .

Ковариация

Для непрерывных случайных величин:

Для независимых и

Если - то случайные величины некоррелированные, иначе коррелированны.

- коэффициент корреляции, где - дисперсии.

Свойства:

• 

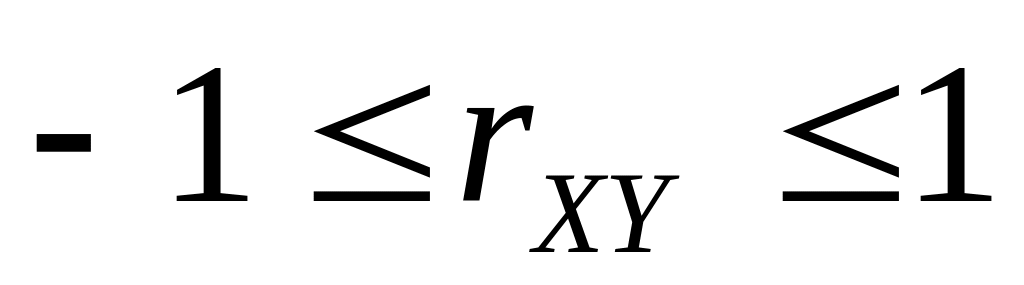
• Если случайные величины Y,X не коррелированны, то

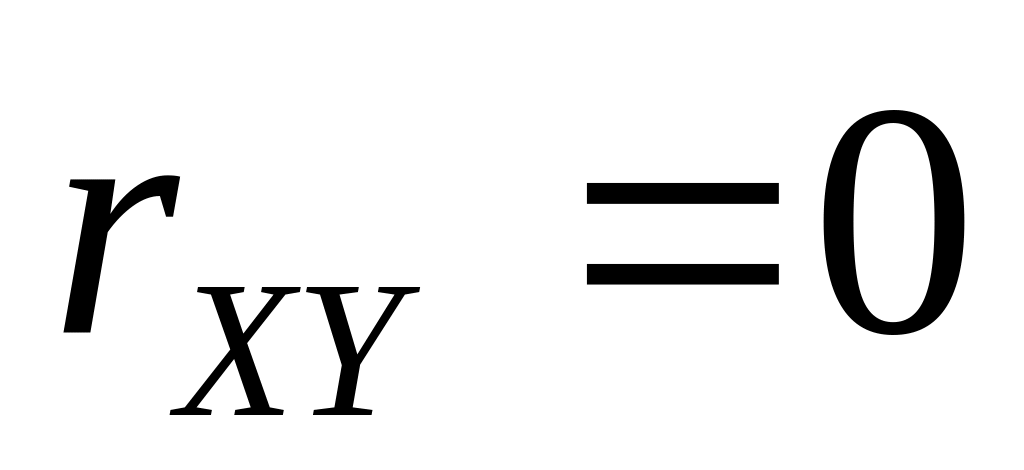
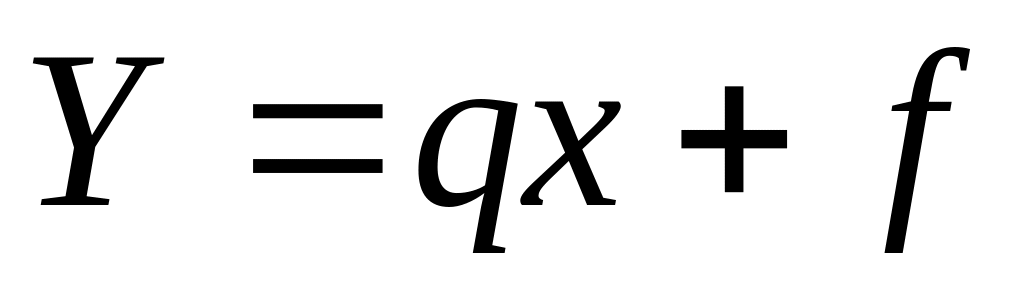• - используя модуль коэффициента корреляции определяется

• Если для двух случайных величин выполняется 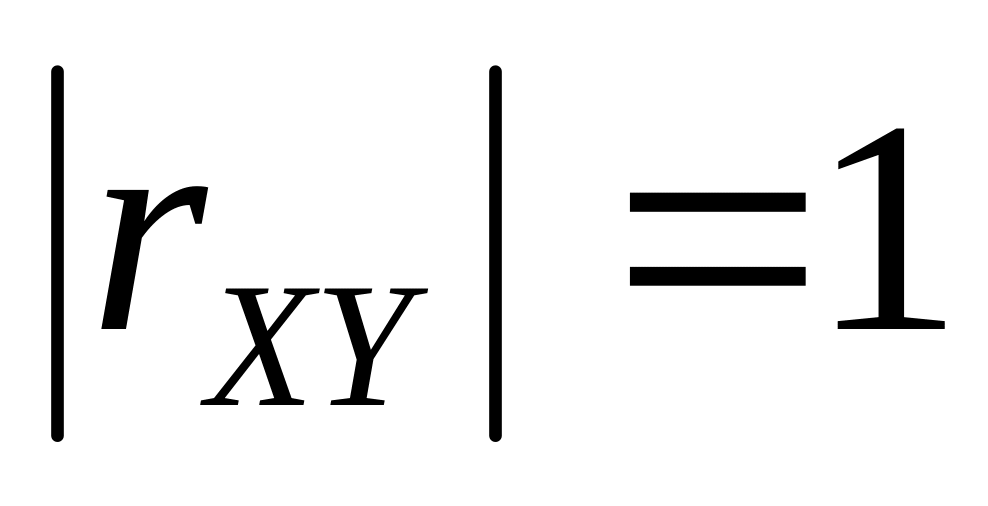, то эти величины максимально коррелированны, для них выполняется и предыдущее.

43. Сходимость по вероятности. Второе неравенство Чебышева.

Скажем что случайные величины - сходятся по вероятности к величине A случайной или неслучайной, если для выполняется

Сходимость по вероятности требует, чтобы неравенство выполнялось, для подавляющего числа членов последовательности, а в обычном мат. анализее для всех .

Второе неравенство Чебышева.

Если случайная величина X имеет мат. ожидание и , то для выполняется .

Для вероятности имеем

, где

- второе неравенство Чебышева в другой форме.

44. Правило трех сигм. Теорема Маркова.

Для нормального распределения - правило трех сигм для нормального распределения вероятностей.

С помощью неравенства Чебышева оценить вероятность того, что отклонение X от a, будет меньше трех сигм.

- правило трех сигм для произвольного распределения вероятностей.

Теорема Маркова. Для любой неотрицательной случайной величины X имеющей мат ожидание M(X) и выполняется неравенство: (Неравенство Маркова или первое неравенство Чебышева)

- иная форма.

45. Теорема Чебышева. Закон больших чисел. Центральная предельная теорема (теорема Ляпунова).

Теорема Чебышёва: Для независимых случайных величин соотношение 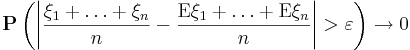(при любом и ) верно при весьма общих предположениях:

Закон больших чисел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.

Всегда найдётся такое количество испытаний, при котором с любой заданной наперёд вероятностью относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности.

Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.

Центральная предельная теорема (теорема Ляпунова): Пусть случайные величины {X_i} имеют конечный третий момент. Тогда определена последовательность . Если предел (условие Ляпунова), то по распределению при .