5. Возведение в степень

6. Извлечение корня 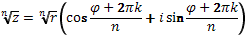– формула Муавра

12. Последовательности комплексных чисел. Сходимость последовательности комплексных чисел.

Последовательность комплексных чисел можно рассматривать как отображение в C множества натуральных чисел N, т.е. как функцию целого положительного аргумента n, принимающую комплексные значения .

Комплексное число a называют пределом последовательности комплексных чисел и записывают , если для любого можно найти натуральное число N, такое, что при все элементы последовательности попадают в - окрестность точки a.

. В - окрестности бесконечно много элементов

Под - окрестностью точки понимается область заключенная внутри круга с центром и радиусом .

Последовательность комплексных чисел, имеющую своим пределом комплексное число , называют сходящейся в точке a. Это число может быть действительным или чисто мнимым.

13. Функции комплексных переменных. Основные элементарные функции комплексного переменного.

Функции комплексных переменных – функция комплексного переменного, имеющая комплексные значения . Такая функция может быть представлена в виде . Для того, чтобы функция f(x) была дифференцируема, должны выполнятся условия Коши-Римана: , .

1. Дробно-рациональная функция :

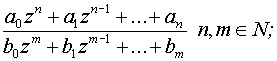   1. линейная функция

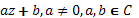
   2. степенная функция с натуральным показателем

   3. дробно-линейная функция

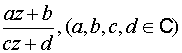
2. Показательная функция 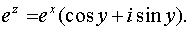, причём на показательную функцию комплексного переменного переносится теорема сложения . Показательная функция комплексного переменного является периодической функцией с основным периодом , т.е. .

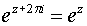3. Тригонометрические функции:

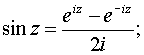
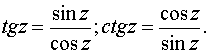
4. Гиперболические функции:

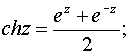
5. Логарифмическая функция 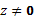, , 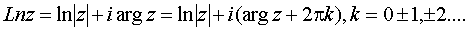она определяется как обратная к показательной функции. Так как показательная функция – периодическая с периодом, то логарифмическая функция является многозначной. В каждой точке 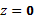она принимает бесконечно много значений. Функция , где arg z – главное значение аргумента, называется главным значением логарифмической функции. Поэтому 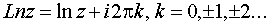Известные правила о логарифме произведения и частного сохраняют свою силу и для многозначного логарифма, а именно: при z1 и z2, отличных от нуля, верны формулы

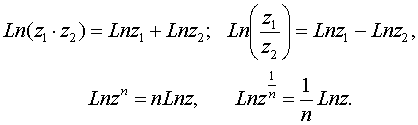
6. Общая степенная функция: 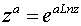, где . Эта функция многозначная, её главное значение равно 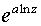. При 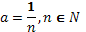получаем многозначную функцию – корень n-й степени из z:

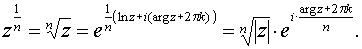
14. Производная функции комплексного переменного. Условия Даламбера-Эйлера. Определение аналитической функции. Дифференциал. Производная элементарной функции.

Производная функции комплексного переменного.

Пусть w = f (z) определена в точке z = x + yi и некоторой ее окрестности. Пусть x получает некоторое приращение ∆x, а y – приращение ∆y . Тогда ∆z = ∆x + i∆y – соответствующее приращение переменной z. Пусть ∆w = f (z +∆z) − f (z).

Определение. Если существует предел вида , то он называется производной

функции f (z) в точке z; обозначается

Функция же f (z) называется дифференцируемой в точке z.

Необходимыми и достаточными условиями дифференцируемости f (z) в точке z являются дифференцируемость функций u x,(y и) v x,(y в) точке (x, y) и выполнимость следующих условий Коши-Римана(Даламбера-Эйлера):

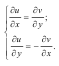
Производная дифференцируемой функции может быть записана по одной из формул:

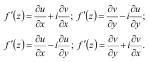
Дифференциал

Определения анал.ф.: Функция w = f (z), дифференцируемая в точке z₀ и некоторой ее окрестности, называется аналитической в точке z₀ .

Функция, аналитическая во всех точках некоторой области G, называется аналитической в этой области.