4. Задачи для учащихся, готовящихся к олимпиаде по физике

З адача 16. Шарик, подвешенный на нити длиной L=1 м, вращают в горизонтальной плоскости так, что нить образует с вертикалью угол  =30⁰(конический маятник). Определить угловую скорость  и частоту вращения шарика n, если маятник находится в кабине, движущейся вертикально вверх с ускорением a = 5 м/с².

Решение

1. Решаем задачу в инерциальной системе отсчета, связанной с Землей. Выбираем систему координат так, чтобы одна из осей (в данном случае ось У) совпала с ускорением а, и составляем динамические уравнения относительно каждой из осей:

на ось У: Т Cos  - mg= ma, или Т Cos  = mg + ma;

на ось Х: Т Sin  = m a_n, или Т Sin  = m ²r.

С учетом того, что радиус вращения шарика равен r = L Sin , получаем Т Sin  = m ²L Sin , или Т = m ² L.

Итак, получили два уравнения: Т Cos  = mg + ma,

Т = m ² L.

Выполнив почленное деление уравнений одного на другое, получаем Cos  = . Отсюда находим  = . Подставив данные величины, получаем  = 4,1 с^-1. Частота вращения равна n = об/с; n = 0,65 об/с = 39 об/мин.

2. Решаем эту же задачу в неинерциальной системе отсчета, связанной с кабиной. Тогда решение абсолютно идентично решению задачи 15 с той лишь разницей, что ускорение g заменяется относительным (или эквивалентным) ускорением g' = g – a , что в скалярном виде дает выражение g' = g + a (рис. 16). Тогда получаем тот же результат  = = .

Ответ: угловая скорость вращения шарика стала равной 4,1 с^-1, а частота вращения увеличилась до 39 об/мин.

Задача 17. Полая сфера радиусом R = 25 см вращается во­круг вертикальной оси, проходящей через центр сферы (рис. 17). Внутри сферы находится маленький шарик, вра­щающийся вместе с ней. Определить высоту, на которую поднимается шарик при частоте вращения, равной

n = 110 об/мин = об/с.

Решение

Вращение шарика в сфере фактически является о коническим маятником. Значит и решение аналогично решению предыдущих задач. Но мы рассмотрим

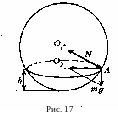еще один вариант решения подобных задач.

По условию шарик не­подвижен относительно сферы. Значит, шарик движется по окружности с центром в точке О₂.

На шарик действуют две силы: mg и сила реакции опоры N. Равнодействующая сил N и mg направлена согласно второму закону Ньютона, как и нормальное ускорение а_n, т. е. к центру O₂.

На рис 15 треугольник, образованный век­торами сил, и треугольник «геометрический» О₂AО₁ с ка­тетом О₂А. Из подобия этих треугольников можно полу­чить уравнение для искомой величины. Из подобия треугольников следует, что = , где R – радиус сферы, h – искомая высота подъема, r – радиус окружности; (R- h)a_n = rg, h = R - . Так как а_n = ω²r = (2πn)²r, h = R – = 17,4 см.

Ответ: 17,6 см.

З адача 18. Космонавты, вы­садившиеся на поверхности Марса, из­мерили период вращения конического маятника, оказавшийся равным Т = 3 с. Длина нити L= 1 м. Угол, образованный нитью с верти­калью, равен α =30^o. Найдите по этим данным ускорение свободного падения на Марсе.

Решение

Тело движется по окружности радиу­сом Lsin α с угловой скоростью и с ускорением a = ( )² Lsin α.

На тело массой m действуют сила натя­жения нити F_H и сила тяготения, равная mg', где g' — ускорение свободного падения на Марсе.

Уравнение движения тела имеет вид F_H + mg' = ma. Из рисунка видно, что = tg α или = tg α.

Подставив в последнее равенство выра­жение для а, находим ускорение свобод­ного падения на Марсе: g '= ( )² Lcosα ≈ 3,8 м/с².

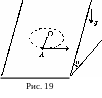Задача 19. На гладкой наклонной плоскости с углом наклона α к горизонту в точке О закреплена нить длиной l; к другому концу нити привязан небольшой ша­рик. В начальный момент ша­рик находится в положении равнове­сия в точке А (рис. 19). Какую минимальную скорость надо сообщить шарику в точ­ке А вдоль наклонной плоскости в горизонтальном направлении, чтобы шарик совершил полный оборот, дви­гаясь по окружности?

Решение

Шарик сможет совершить полный оборот, если в верхней точке натяжение нити будет больше или равно 0. Минимальная скорость в точке А соответствует Т=0 в верхней точке траектории. Для верхней точки траектории динамическое уравнение имеет вид mg sin α + T = m или mg sin α = m при Т= 0; v² = glsin α.

Тогда в нижней точке по закону сохранения энергии относительно горизонтали, проведенной через точку А, принятой за нулевой потенциальный уровень, m + 2mgl sin α=m ; v_A² = 5gl sin α. Отсюда .

З адача 20. Максимально допустимая скорость автомобиля при прохождении поворо­та на горизонтальной дороге радиусом R=100 м равна 36 км/ч. Какова должна быть максимальная скорость прохождения автомобилем такого же поворота с таким же дорожным покрытием, если дорога наклонена под углом 30° к гори­зонту?

Решение

Так как максимально допустимая скорость движения автомобиля на повороте радиуса R равна (см. задачу 1) = 10 м/с, находим коэффициент трения колес о дорожное покрытие μ = 0,1.

На автомобиль действуют: сила тяжести mg, реакция плоскости N, сила трения F_тр= μN.

Спроецируем силы на указанные на рисунке 20 координатные оси Х и У: Ncos α + F_трsin α = mg; или N (cos α+ μ sin α) = mg;

-N sin α + μ Ncos α= -m ; или N (sin α - μ cos α)= m .

Поделив уравнения друг на друга почленно, получаем м/с.

Ответ: максимальная скорость прохождения автомобилем наклонного поворота 76 км/ч.

Итак, задачи подобного типа могут быть усложнены наличием разных по природе и направлению сил. Обязательным при решении должен быть выбор удобной системы отсчета (инерциальной или неинерциальной) и системы координат, на оси которой нужно спроецировать все действующие на тело силы (или равнодействующую всех этих сил). Это позволит составить динамические уравнения. А решение этих уравнений может быть различным – как алгебраическим, так и геометрическим. Важно только знать и правильно применять условия возникновения тангенциального и нормального ускорений.