§ 7. Применение ду с разделяющимися переменными: задачи из физики

Задачи из физики интересны тем, что они «моделируют» процессы исследования физического явления, демонстрируют возможности математического анализа при решении физических (и инженерных!) задач. Также важно то, что общее решение в таких задачах воспринимается как общий метод решения (как расчетная формула), а частное решение – как применение решения к конкретным условиям физического процесса.

☺☺

Пример 1–21: Пуля, двигаясь со скоростью v₀=400 м/с, пробивает стену толщиной h=20 см и вылетает из нее со скоростью v₁=100 м/с. Полагая силу сопротивления стены пропорциональной квадрату скорости движения пули, найти время Т движения пули в стене.

Решение:

Направление оси координат ОХ и векторов скорости соответствуют рисунку. Учитывая, что сила сопротивления материала стены направлена против движения пули, в соответствии с законом Ньютона, запишем дифференциальное уравнение:

mv′= –kv², или mdv = –kv²dt. (1)

0). Запишем уравнение в виде: mdv = – kv²dt =0 – уравнение с разделяющимися переменными.

1). Учитывая Случай-В, запишем решение, которое следует из исходной записи уравнения: v =0. Для заданных исходных данных это решение нам не потребуется!

2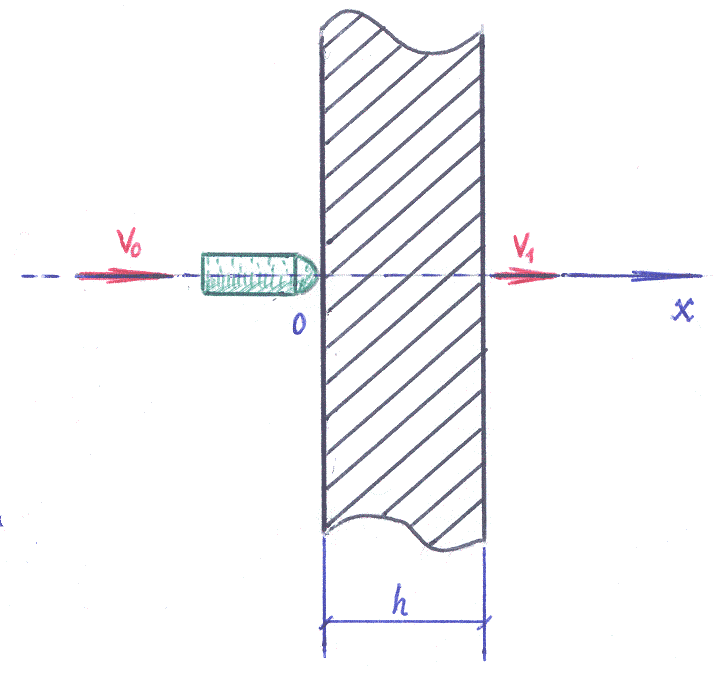 ). Учитывая, что теперь v ≠0, запишем уравнение в виде: =–kdt; «видим!»: переменные разделились → можно приступить к интегрированию ДУ!

3). Интегрируем: m =–kt +C или =kt +C. Так как при t=0 скорость пули равна v₀, то величина С= . При t=Т скорость пули равна v₁, получаем уравнение: =kТ+ . Из последнего имеем: Т= . (2)

Замечание: Рассчитать время Т по формуле (2) невозможно, так как неизвестно отношение массы к коэффициенту сопротивления k.

4). Учитывая: v= , приведем уравнение =kt+ к виду: m =kt+ , или (умножая на v₀ и деля на m): v₀dt= dx, или (принимая k₁= ): v₀dt =(v_0∙k_1∙t+1)dx, или (разделяя переменные): =k₁dx → можно приступить к интегрированию ДУ!

5). Интегрируем: =k₁x +C₁, или ln(v_0∙k_1∙t+1)=k₁x +C₁. Так как при t=0 координата х=0, то С₁=0.

6). Из выражения (2) легко получить: v_0∙k_1∙Т+1= . Но для t=Т имеем: ln(v_0∙k_1∙Т+1)=k₁h, или ln = k₁h. отсюда: = .

7). Теперь можно записать формулу для вычисления времени движения пули в стене при заданных условиях: Т= → для заданных скоростей v₀, v₁ и h получим: Т ≈ 0.00108 с.

Ответ: Т ≈ 0.00108 с.

Замечание: важно при решении задачи выделить два принципиально важных момента:

1). Выбор модели физического процесса: сила противодействия стены «пропорциональна квадрату скорости» определяется как результат физических экспериментов.

2). Получение формулы (2), которую можно применять для заданной пули и стены также потребовало измерений скорости пули на входе в стену и на выходе.

Пример 1–22: Пусть имеется сосуд, наполненный жидкостью до уровня Н. Известна зависимость площади S поперечного сечения от высоты h: S=S(h). В дне сосуда имеется отверстие, площадь которого ω. Через это отверстие жидкость вытекает. Необходимо определить время t, за которое уровень жидкости понизится с начального уровня Н до произвольного уровня h. Также необходимо определить время Т полного опорожнения сосуда. Будем считать, что скорость v истечения жидкости из сосуда является известной функцией v =v(h) от уровня h жидкости в сосуде (напора).

Решение:

Пусть высота жидкости в сосуде в некоторый момент времени t равна h. Количество жидкости dV, вытекшее из сосуда за промежуток времени dt от момента t до t+dt, можно вычислить как объём цилиндра с площадью основания ω и высотой vdt, То есть:

dV = ωv(h)dt. (1)

С другой стороны, этот же объём можно вычислить, проследив понижение уровня жидкости в сосуде (учтено dh<0): dV = – S(h)dh. (2)

И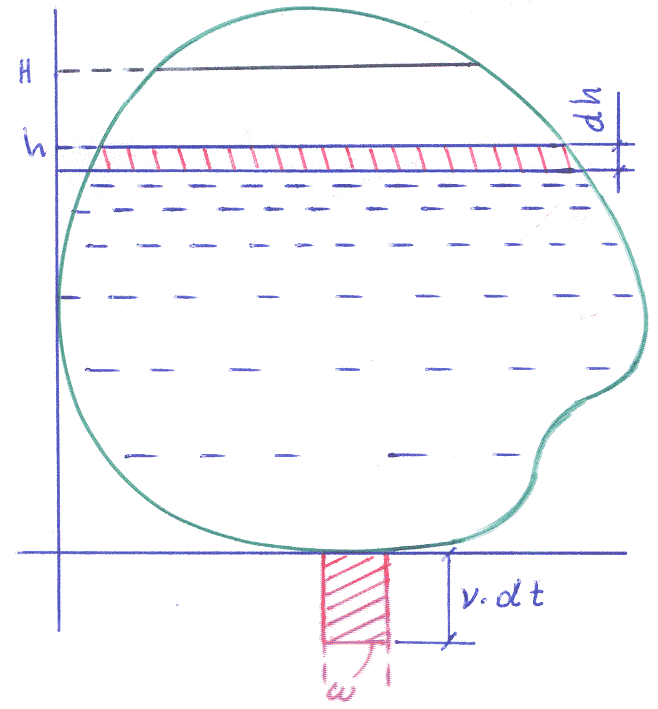 з выражений (1) и (2): ωv(h)dt = – S(h)dh. (3)

0). Запишем уравнение в виде: ωv(h)dt = – S(h)dh – уравнение с разделяющимися переменными.

1). Учитывая «Решение–В», запишем решение, которое следует из исходной записи уравнения: v (h) =0. Для заданных исходных данных это решение нам не потребуется!

2). Учитывая, что теперь v ≠0, запишем уравнение в виде: dt=– ; «видим!»: переменные разделились → можно приступить к интегрированию ДУ!

3). Интегрируем: t=– = . Полное истечение жидкости из сосуда произойдет за время: Т= . (4)

Замечание: Если истечение жидкости происходит через малое отверстие (или короткий патрубок), то v=μ , где g–ускорение силы тяжести, μ – эмпирический коэффициент (коэффициент расхода).

Ответ: время опорожнения сосуда до уровня h: t= . Время полного опорожнения сосуда потребует времени: Т= .

Пример 1–23: Определить время опорожнения сосуда конической формы, заполненного водой. Форма сосуда соответствует рисунку: D₁=0.8м; D₂=0.3м; Н=1м; a=0.03м; μ=0.62 (для воды). Замечание: используются результаты Примера 1–22.

Р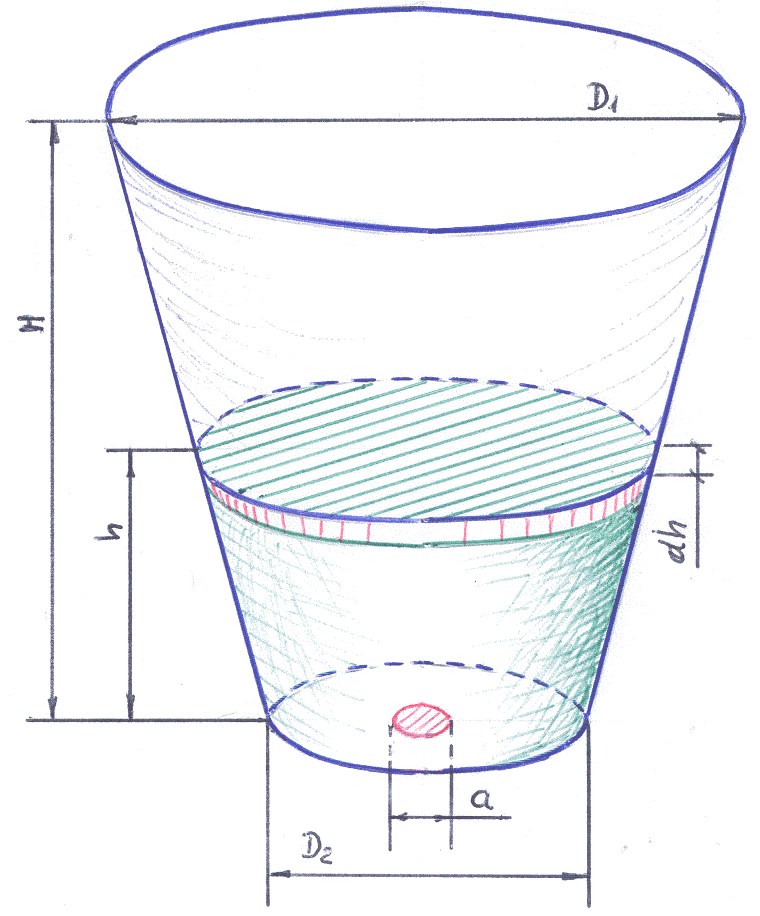 ешение:

Для определения площади S(h) свободной поверхности жидкости на уровне h необходимо вычислить радиус круга на этом уровне.

Используя подобие треугольников, этот радиус легко найти:

R(h)= R₂+(R₁–R₂) = ( D₂+(D₁–D₂) ).

Используя исходные данные, запишем выражение: R(h)=0.05(3+5 h), после чего получаем:

S(h)=πR²(h)=π(0.05(3+5 h))².

Вычислим площадь отверстия, через которое вытекает жидкость: ω=π = π0.000056.

Запишем выражение для скорости истечения жидкости для заданных условий:

v=μ =0.62 =2.77 .

Теперь запишем формулу для вычисления времени опорожнения сосуда:

Т= = ≈ 3мин 14с.

Замечание: Если предполагается многократное применение расчетной формулы, то удобнее выполнить интегрирование в общем виде: Т= (3 +4D₁D₂+8 ), после чего подставлять в эту формулу конкретные исходные данные.

Ответ: Т≈ 3мин 14с.

☻