Занятие 1. Основные понятия. Теорема о существовании и единственности решения ду 1-го порядка. Уравнения первого порядка с разделяющимися переменными.
Ауд. |
Л-3 |
гл.10: № 1, 3, 4, 6, 9, 16, 17, 23, 25, 26, 30, 31, 38, 41, 43, 167. |
16 |
☺ ☻ ☺
Пример 1–1: Показать, что при любом действительном значении параметра С заданная функция y=x(C–ln|x|) является решением ДУ: (x–y)dx + xdy=0.
Решение:
1). Разделим уравнение на dx. Получаем уравнение в виде: x–y + xy′=0. (1)
2). Для
нахождения производной заданной функции
вспомним: (ln|x|)′=
∙|x|′=
.
Тогда запишем: y′=
C–ln|x|–x
=
C–ln|x|–1.
3). Подставим заданную функцию y и ее производную y′ в уравнение (1):
x– x(C–ln|x|)+x(C–ln|x|–1)=0 → тождество.
4). Это значит, что заданная функция является решением заданного ДУ.
Ответ: заданная функция является решением заданного ДУ.
Пример 2–3: Показать, что при любом действительном значении параметра С заданная функция 2x+y–1=Ce2y–x является решением ДУ: (2x+y+1)dx –(4x+2y–3)dy=0.
Решение:
1). Разделим уравнение на dx. Получаем уравнение в виде: 2x+y+1–(4x+2y–3)y′=0.
2). При нахождении производной заданной функции учтем, что функция y=y(x) в нашем примере задана неявно. Дифференцируем выражение 2x+y–1=Ce2y–x по x; учитывая y=y(x), получим:
2+y′= Ce2y–x∙(2y′–1)=[учтем, что Ce2y–x=2x+y–1]=( 2x+y–1)∙(2y′–1),
или, применяя тождественные преобразования: (4x+2y–3)y′=2x+y+1.
3). Подставив заданную функцию y и ее производную y′ в уравнение (1), получаем очевидное тождество: 2x+y+1–(2x+y+1)=0
4). Это значит, что заданная функция является решением заданного ду.
Ответ: заданная функция является решением заданного ДУ.
Пример 3–4: В заданном семействе: y(ln|x2–1|+C) =1 выделить уравнение кривой, удовлетворяющей приведенному начальному условию: y(0)=1.
Решение:
1). Выделить из семейства кривых кривую, которая проходит через точку (0,1) – это значит вычислить значение С, при условии, что х=0, y =1.
2). Подставим х=0, y=1 в выражение семейства: 1∙(ln|02–1|+C) =1, откуда C) =1.
3). Запишем выражение кривой семейства, проходящей через точку (0,1): y(ln|x2–1|+1) =1.
Ответ: y(ln|x2–1|+1) =1.
Пример 4–6: В заданном семействе y=2+Ccosx выделить уравнение кривой, удовлетворяющей приведенному начальному условию: y(0) = –1.
Решение:
1). Выделить из семейства кривых кривую, которая проходит через точку (0,–1) – это значит вычислить значение С, при условии, что х=0, y= –1.
2). Подставим х=0, y= –1 в выражение семейства: –1=2+Ccos0, откуда C) = –3.
3). Запишем выражение кривой семейства, проходящей через точку (0,–1): y=2–3cosx.
Ответ: y=2–3cosx.
Пример 5–9: Составить дифференциальное уравнение семейства парабол: y = x2+2ax.
Решение:
1). Преобразуем выражение семейства (известная операция выделения полного квадрата): y=(x+a)2–a2. При непрерывном изменении параметра a ось параболы y = x2 смещается влево при a > 0 и вправо при a < 0; одновременно вершина параболы движется по параболе y = –a2.
2). Вычислим производную y′ для заданного семейства: y′=2x+2a.
3). Для получения ДУ нужно исключить параметр a из выражения y=x2+2ax или y′=2x+2a:
а) умножим второе на x, получим: xy′=2x2+2ax=x2+2ax+x2= y +x2;
б) получено ДУ: xy′= y +x2.
Ответ: xy′= y +x2.
Пример 6–16: Методом изоклин построить приближенно семейство интегральных кривых для дифференциального уравнения: y′=x+y.
Р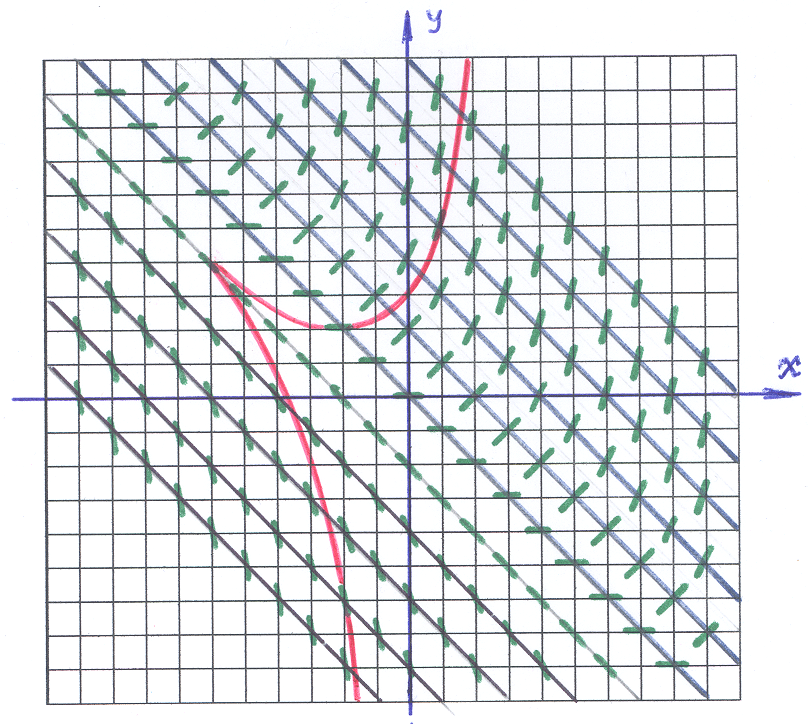
ешение:
1). Уравнение изоклин для заданного ДУ получается приравниванием y′=k. В нашем случае каждая изоклина – прямая: k=x+y. На рисунке изоклины выделены «синим» цветом. На каждой изоклине черточка («зеленая») отражает конкретное значение k, определяющее изоклину, то есть: на каждой изоклине наклон черточки один и тот же.
2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемая «интегральная кривая» (одна из них выделена «красным» цветом), то есть «решение» заданного ДУ.
Ответ: интегральная кривая представлена на рисунке.
Пример 7–17: Методом изоклин построить приближенно семейство интегральных кривых для дифференциального уравнения: y′=1+y.
Р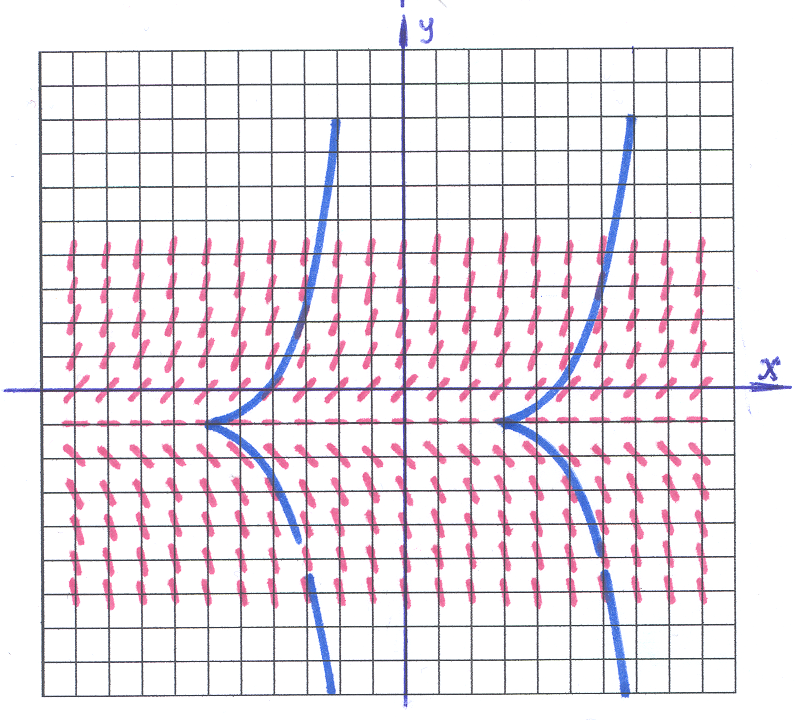
ешение:
1). Уравнение изоклин для заданного ДУ получается приравниванием y′=k. В нашем случае каждая изоклина – прямая: k=1+y. На рисунке изоклины выделены «серым» цветом: прямые, параллельные оси ОХ. На каждой изоклине черточка («красная») отражает конкретное значение k, определяющее изоклину, то есть: на каждой изоклине наклон черточки один и тот же.
2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемая «интегральная кривая» (одна из них выделена «синим» цветом), то есть «решение» заданного ДУ.
Ответ: интегральная кривая представлена на рисунке.
Пример 8–23: Решить дифференциальное уравнение: y2y′ + x2=1.
Решение:
0). Запишем уравнение в виде: y2dy =(1–x2)dx, «видим» – уравнение с разделяющимися переменными.