9 Ду. Занятие 5
ЗАНЯТИЕ 5. Уравнения первого порядка, не разрешенные относительно производной.
Ауд. |
Л-3 |
гл.10: № 114, 116, 118, 120, 122,124. |
6 |
☺ ☻ ☺
Пример 1–114: Найти общее решение уравнения: y=(y′)2+4(y′)3 в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: y=φ(p)=p2+4p3.
a2.
Учитывая: y′=
,
запишем dy=φ′(p)dp,
где: φ′(p)=2p+12p2.
Получаем уравнение для нахождения x:
dx=
dp=(2+12p)dp.
a3.
Запишем выражение для x:
x=
+С=2p+6p2+С.
a3.
Составляем систему:
,
или
–
параметрическое решение.
a4. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ:
–
общее решение в параметрической форме.
Решение y=0 –
особое.
Пример 2–116: Найти общее решение уравнения: y=(y′–1)ey′ в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p) =(p–1)ep.
a2. Учитывая: y′= , запишем dy=φ′(p)dp, где: φ′(p)=pep. Получаем уравнение для нахождения x: dx= dp=epdp.
a3.
Запишем выражение для x:
x=
+С=ep
+С.
a4.
Составляем систему:
,
или
–
параметрическое решение.
a5. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ:
– общее решение в
параметрической форме.
Пример 3–118: Найти общее решение уравнения: x=y′3–y′+2 в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: x=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: x=φ(p)=p3–p+2.
a2. Учитывая: y′= , или dy=pdx, запишем dx=φ′(p)dp, где: φ′(p)=3p2–1. Получаем уравнение для нахождения y: dy=pφ′(p)dp=(3p3–p)dp.
a3.
Запишем выражение для y:
y=
+С=
p4–
p2+С=μ(p)+С.
a4.
Составляем систему:
,
или
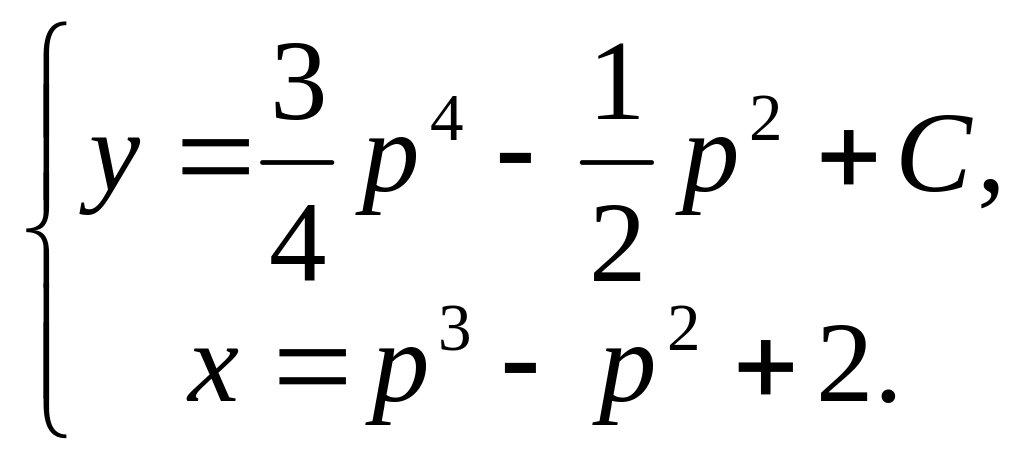
a5. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: – общее решение в параметрической форме.
Пример 4–120: Найти общее решение уравнения: x=2y′–lny′ в параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: x=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p. Тогда исходное уравнение принимает вид: x=φ(p)=2p–lnp.
a2.
Учитывая: y′=
,
или dy=pdx,
запишем dx=φ′(p)dp,
где: φ′(p)=2–
.
Получаем уравнение для нахождения y:
dy=pφ′(p)dp=(2p–1)dp.
a3.
Запишем выражение для y:
y=
+С=p2–p+С=μ(p)+С.
a3.
Составляем систему:
,
или
a4. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: – общее решение в параметрической форме.
Пример 5–122:
Найти решение уравнения Лагранжа: y=x
,
применяя метод введения параметра.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′)∙x+ψ(y′), где φ(y′)= и ψ(y′)=0.