
- •9 Ду. Занятие 5
- •Данное уравнение решаем, применяя общий алгоритм:
- •Данное уравнение решаем, применяя общий алгоритм:
- •Данное уравнение решаем, применяя алгоритм введения параметра:
- •Данное уравнение решаем, применяя общий алгоритм:
- •Применим общий алгоритм введения параметра:
- •Данное уравнение решаем, применяя общий алгоритм:
- •Данное уравнение решаем, применяя общий алгоритм:
Данное уравнение решаем, применяя общий алгоритм:
a1.
Примем y′=p
→ исходное уравнение
принимает вид: y=φ(p)∙x+ψ(p)=x∙![]() .
.
a2.
Дифференцируя последнее
по x имеем: p–φ(p)=[x∙φ′(p)+ψ′(p)]![]() .
.
a3.
Запишем равенство: p–φ(p)=
![]() =0,
его решения: p0=–1
и p0=1.
Учитывая p0 ≡φ(p0),
запишем: а) для p0=–1:
y=φ(p0)∙x+ψ(p0)
→ y=–1∙x+0=–x;
=0,
его решения: p0=–1
и p0=1.
Учитывая p0 ≡φ(p0),
запишем: а) для p0=–1:
y=φ(p0)∙x+ψ(p0)
→ y=–1∙x+0=–x;
б) для p0=1: y=φ(p0)∙x+ψ(p0) → y=1∙x+0= х.
Пока не получено общее решение уравнения, мы не можем сказать, будут эти решения особыми, или нет.
a4. Пусть теперь p–φ(p) ≠ 0. Запишем уравнение для вычисления x:
![]() –x
–x![]() =
=![]() ,
или
–
x
,
или
–
x![]() =
,
или
=
–(x+1)
=
,
или
=
–(x+1)![]() .
.
a5.
Теперь p–φ(p)≠0.
Для нахождения x решим:
–x
=
– линейное уравнение. В нашем случае:
–x![]() ∙
∙![]() =0,
или
=
x
:
уравнение с разделяющимися переменными
→ p = Cx.
=0,
или
=
x
:
уравнение с разделяющимися переменными
→ p = Cx.
a6.
Cистема:
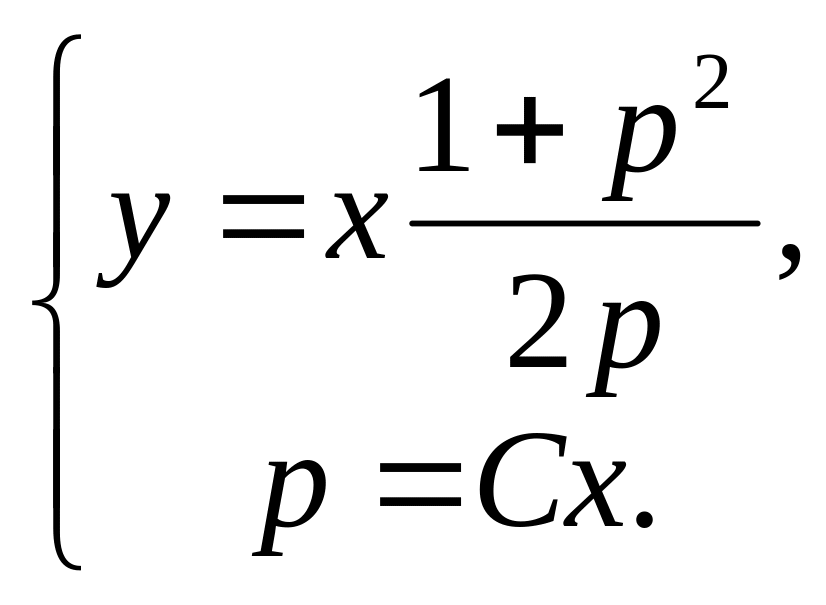 легко приводится к виду → y=
легко приводится к виду → y=![]() Cx2+
Cx2+![]() – общий интеграл заданного уравнения.
– общий интеграл заданного уравнения.
Ответ: y= Cx2+ – общий интеграл заданного уравнения. Особое решение: y = ±x.
Пример 6–124: Найти решение уравнения Лагранжа: y=x(y′)2+(y′)3, применяя метод введения параметра.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′)∙x+ψ(y′), где φ(y′)=(y′)2 и ψ(y′)=(y′)3.
Данное уравнение решаем, применяя общий алгоритм:
a1. Примем y′=p → исходное уравнение принимает вид: y=φ(p)∙x+ψ(p)=x∙p2+p3.
a2. Дифференцируя последнее по x имеем: p–φ(p)=[x∙φ′(p)+ψ′(p)] . В нашем случае это равенство: p–p2=[x∙2p+3p] .
a3. Запишем равенство: p–φ(p)=p–p2=0, его решения: p0=0 и p0=1. Учитывая p0 ≡φ(p0), запишем: а) для p0=0: y=φ(p0)∙x+ψ(p0) → y=0∙x+0=0;
б) для p0=1: y=φ(p0)∙x+ψ(p0) → y=1∙x+1= х+1.
Пока не получено общее решение уравнения, мы не можем сказать, будут эти решения особыми, или нет.
a4.
Теперь p–φ(p)≠0.
Для нахождения x решим:
–x
=
– линейное уравнение. В нашем случае:
–x![]() =
=![]() =0,
или
+
=0,
или
+![]() x=–
x=–![]() .
.
Данное линейное уравнение решаем, применяя общий алгоритм:
a5. Решение уравнения ищем в виде функции: x=u∙v.
a6.
Вычислим: –![]() =–
=–![]() =–2ln|p–1|,
и запишем: u=
=–2ln|p–1|,
и запишем: u=![]() ,
то есть u
=
,
то есть u
=![]() .
.
a8.
Вычислим функцию v: v =
![]() +С=
–
+С=
–![]() +С
=
+С
=![]() p2–
p3+С.
p2–
p3+С.
a9. Запишем общее решение линейного уравнения для x:
x=u∙v=
∙![]() =
∙
=
∙![]() +
+![]() .
.
Замечание: если в последнем выражении в первой дроби выполнить операцию «выделение целой части», то выражение существенно упростится: x= –p– + .
a10.
Если в выражение:
y=x∙p2+p3
подставить выражение для
x,
то для y
получим выражение через параметр p:
y=
–
p2+![]() .
.
a11.
Составляем систему:
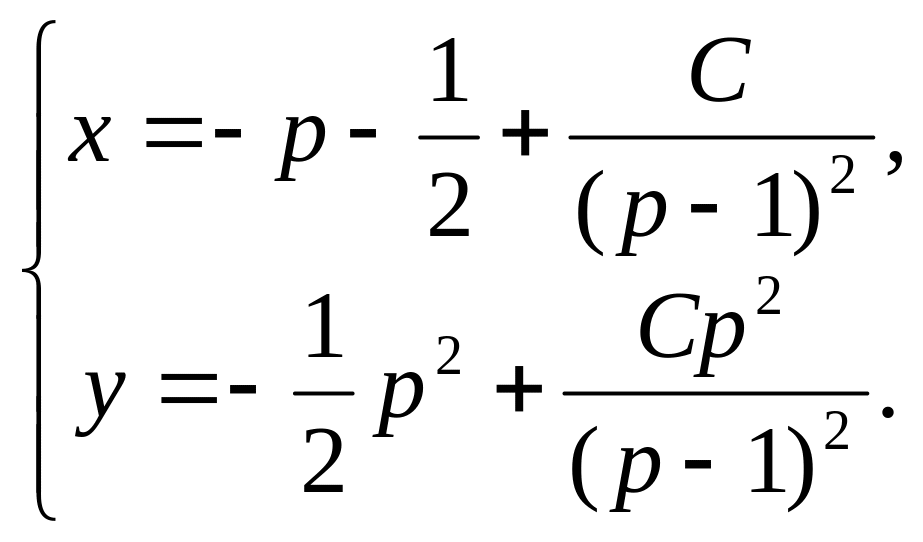 Это решение уравнения в параметрической
форме.
Это решение уравнения в параметрической
форме.
a12. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: – решение уравнения в параметрической форме. Особые решения: y=0; y =x+1.
* * * * * * * * * *
Домашнее задание
Дома |
Л-3 |
гл.10: № 115, 117, 119, 121, 123,125, 177. |
7 |
Пример 1–115:
Найти общее решение уравнения: y=y′
![]() в
параметрической форме.
в
параметрической форме.
Решение:
a0. Форма записи уравнения имеет вид: y=φ(y′).
Данное уравнение решаем, применяя общий алгоритм:
a1.
Примем y′=p.
Тогда исходное уравнение
принимает вид:
y=φ(p)=p![]() .
.
a2.
Учитывая: y′=
,
запишем dy=φ′(p)dp,
где: φ′(p)=
+![]() =
=
![]() .
Получаем уравнение для нахождения x:
dx=
dp=(
.
Получаем уравнение для нахождения x:
dx=
dp=(![]() +
+![]() )dp.
)dp.
a3.
Запишем выражение для x:
x=![]() +
+![]() +С=J1+J2+С.
Вычислим интегралы:
J1=
+С=J1+J2+С.
Вычислим интегралы:
J1=
![]() =[Замена:p2=t]=
=[Замена:p2=t]=
![]() =[Замена:
=[Замена:![]() =u]=
=u]=![]() =lnp–ln(1+
),
=lnp–ln(1+
),
J2=2 . Окончательно: x=2 +lnp–ln(1+ )+С.
a3.
Составляем систему:
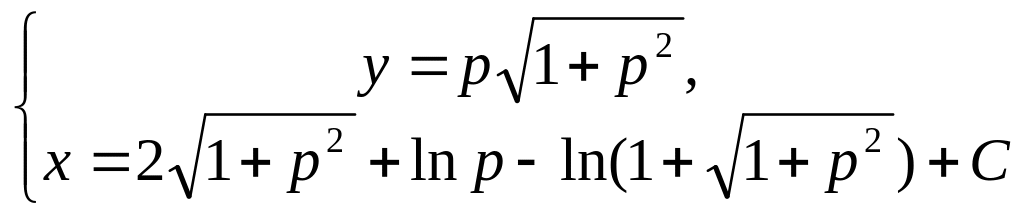 –
общее решение уравнения в параметрической
форме.
–
общее решение уравнения в параметрической
форме.
a4. Пробуем исключить из системы параметр p → F(x,y,C)=0 – общий интеграл. В нашем случае «можно не пробовать»!
Ответ: – общее решение в параметрической форме. Решение y=0 – особое.
Пример 2–117:
Найти общее решение уравнения: y=![]() +2xy′+x2.
+2xy′+x2.
Решение:
a0. Форма записи уравнения имеет вид: y=F(x,y′): не отвечает ни одной из рассмотренных.
