Лекция 1. Основные понятия. Теорема о существовании и единственности решения ДУ 1-го порядка. Уравнения первого порядка с разделяющимися переменными. Однородные функции и однородные уравнения первого порядка. Уравнения специального вида, приводящиеся к однородному ДУ 1-го порядка
Успешное изучение предмета «Дифференциальные уравнения» (кратко ДУ) предполагает устойчивые знания разделов математического анализа: дифференцирование функций одной и нескольких переменных, вычисления неопределенных интегралов. Знание отдельных разделов линейной алгебры и аналитической геометрии также способствует усвоению и активному использованию материала.
§ 1. Основные понятия
В математическом анализе для произвольной функции определены понятия дифференциалов и производных. При дифференцировании заданной функции несколько раз устанавливаются понятия дифференциалов и производных высших порядков. Эти понятия при изучении ДУ являются базовыми. Заметим также, что в изучаемом курсе предполагается, что независимые переменные вещественные.
Определение: (1.1) |
Дифференциальным уравнением называют равенство, содержащее независимые переменные, искомую функцию и ее производные (или дифференциалы). Различают дифференциальные уравнения: 1) обыкновенные: функция зависит только от одной переменной; 2) в частных производных: функция зависит от нескольких переменных. |
Замечание: 1). Мы будем изучать только обыкновенные ДУ.
2). Классификация форм записи ДУ использует в основном обозначения производных. При необходимости переход к форме «записи в дифференциалах» осуществляется по правилам математического анализа.
В общем случае дифференциальное уравнение можно записать в виде:
F(x, y, y′, y′′,… , y(n)) = 0, (1)
где y = y(x) – искомая функция независимой переменной x; y′, y′′,… , y(n) – производные функции по x. Участие в записи ДУ производной y(n) определяет порядок уравнения, а именно: n–й.
В теории ДУ чаще всего используют запись:
y(n)) =f(x, y, y′, y′′,… , y(n–1)) = 0, (2)
уравнение разрешено относительно старшей производной y(n), такую запись называют нормальной формой записи. Уравнение называют линейным, если его форма записи:
y(n)) + a1(x)y(n–1) +… + an-1(x)y′ + any =f(x), (3)
Совокупность уравнений:
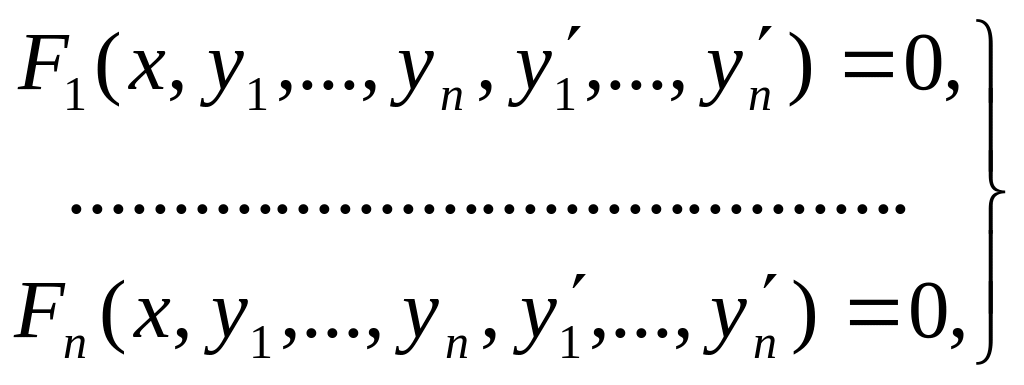(4)
где y1,…,yn – искомые функции от x, называется системой обыкновенных ДУ. Если эта система разрешена относительно производных от искомых функций, то ее называют нормальной системой уравнений:
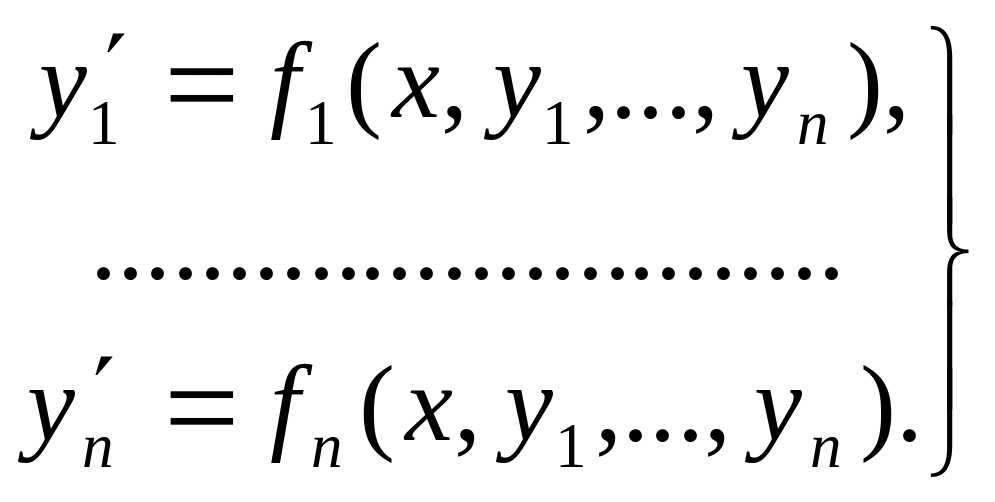(5)
Если нормальная система имеет вид:
(6)
то ее называют линейной.
Пусть заданы дифференциальное уравнение (в любой из форм) и функция y=y(x). Что значит утверждение: функция y=y(x) является решением заданного ДУ?
Определение: (1.2) |
Решением (интегралом) дифференциального уравнения называется всякая функция y=y(x), которая, будучи подставлена в заданное ДУ, превращает его в тождество. |
Процесс нахождения решений ДУ называется интегрированием этого уравнения. Основная задача интегрирования ДУ: найти все решения уравнения и изучить их свойства.
Формы записи решений заданного ДУ могут различаться. Как правило, решения содержат произвольные постоянные. Роль этих постоянных будет уточняться при рассмотрении конкретных ДУ. Для нас в первую очередь важна роль произвольных постоянных в «Задаче Коши».
Пусть имеем ДУ: F(x,y,y′,y′′,…,y(n))=0. Требуется найти решение уравнения y=y(x), которое удовлетворяет дополнительным условиям при заданном числовом значении x 0:
y
=
y0,
y′
=
,
y′′
=
,…
,
y(n–1)
=
. (7)
Такая задача называется Задачей Коши. Числа: x0,y0, , ,…, называют начальными условиями.
Рассмотрим реализацию задачи Коши на простейших уравнениях первого и второго порядков.
Пусть найдено решение ДУ 1-го порядка в форме: y=y(x,С), где С – произвольная постоянная. Геометрически это можно представить как семейство кривых на плоскости OXY, зависящее от одного параметра. Если через каждую точку плоскости проходит кривая семейства, то задача Коши означает выделение из семейства той кривой, которая проходит через точку (x0,y0). Алгебраически это означает решить уравнение: y0=y(x0,С), т.е. найти значение С, выделяющее «нужную» кривую. Следует: для решения задачи Коши в случае уравнения 1-го порядка полученное интегрированием решение должно содержать одну произвольную постоянную.
Пусть найдено решение ДУ 2-го порядка в форме: y=y(x,С1,С2), где С1,С2 – произвольные постоянные. Геометрически это можно представить как семейство кривых на плоскости OXY, зависящее от двух параметров. Если через каждую точку плоскости проходит кривая семейства, то задача Коши означает выделение из семейства той кривой, которая проходит через точку (x0,y0) и имеет заданный угловой коэффициент: . Алгебраически это означает решить систему уравнений: y0=y(x0,С1,С2) и =y′(x0,С1,С2), т.е. найти значения С1,С2, выделяющие «нужную» кривую. Следует: для решения задачи Коши в случае уравнения 2-го порядка полученное интегрированием решение должно содержать две произвольные постоянные.
Обобщение: для решения задачи Коши в случае уравнения n-го порядка необходимо, чтобы решение содержало n произвольных постоянных.
Определение: (1.3) |
Общим решением дифференциального уравнения n-го порядка называют функцию y=y(x,С1,С2,…,Сn), которая зависит от n произвольных постоянных и удовлетворяет условиям: 1). Функция y=y(x,С1,С2,…,Сn) – решение ДУ при любых С1,С2,… , Сn; 2). Для начальных условий: y0, , ,…, в точке (x0,y0) можно определить все С1,С2,… , Сn , обеспечивающие выполнение начальных условий. |
При решении задачи Коши принципиальным моментом является определение произвольных постоянных, обеспечивающих выполнение начальных условий. Алгебраически это требует решения системы уравнений:
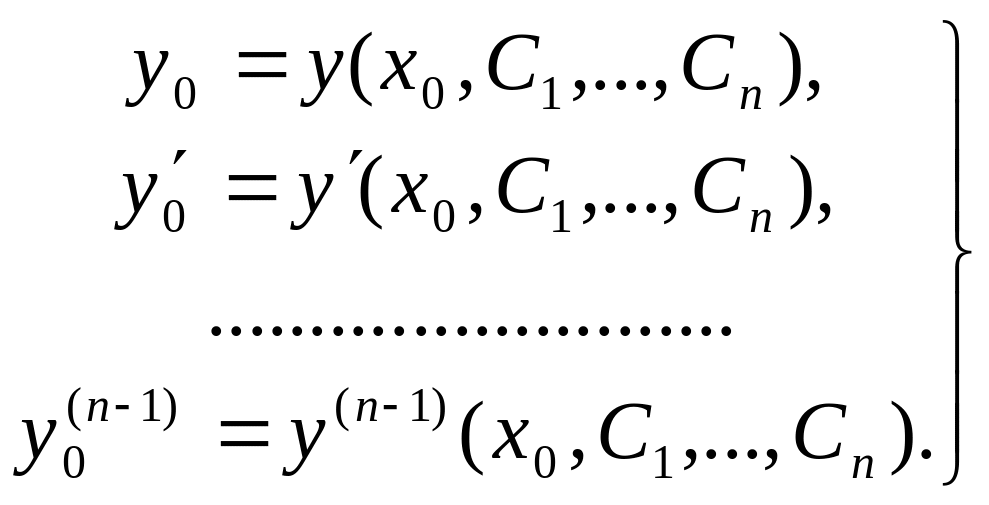(8)
Если заданное ДУ других решений, кроме решения y=y(x,С1,С2,…,Сn) , не имеет и система (8) имеет единственное решение при определении произвольных постоянных С1,С2,…,Сn, то мы «наблюдаем» реализацию «Теоремы о существовании и единственности решения заданного ДУ». Замечание: установление существования и единственности решения для каждого заданного ДУ – непростая задача!
Мы будем рассматривать Теорему о существовании и единственности решения ДУ по мере изучения уравнений различных порядков и типов.