§ 5. Однородные функции

Однородные функции играют важную роль в построении специального типа дифференциальных уравнений 1-го порядка – однородных уравнений.

Определение: (1.5)

Функция f(x,y) называется однородной функцией порядка k относительно переменных x,y, если при любом λ верно: f(λx,λy)= λk f(x, y).

Частный случай составляют однородные функции нулевого порядка: f(λx,λy)= f(x,y). Если для этих функций принять λ= , то получим: f(x,y)= . Это значит, что функция зависит только от отношения независимых переменных x и y.

§ 6. Однородные дифференциальные уравнения

Однородные дифференциальные уравнения интересны тем, что достаточно просто приводятся к уравнениям с разделяющимися переменными, т.е. всегда интегрируются.

Определение: (1.6)

Дифференциальное уравнение называется однородным, если: А. В записи y′=f(x,y) функция f(x,y) – однородная нулевого порядка. В. В записи f1(x,y)dx+f2(x,y)dy=0 функции f1(x,y) и f2(x,y) – однородные функции одного порядка.

Начнем с однородного ДУ типа А, т.к. решение ДУ типа В осуществляется сведением его к решению первого!

Решение–А: учтем, что заданное уравнение можно записать в виде: y′= . (1)

Общая схема решения уравнения y′=f(x,y) такова:

1). Выделяем возможные решения исходного уравнения: f(x,y₀)=0. Это дает одно из решений: y = y₀ – прямая, параллельная оси ОХ.

2). Примем =u(x). Тогда: y=ux → её производная: y′=u′x+u.

3). Подставим в исходное уравнение (1) функцию y=ux и её производную y′=u′x+u. Получим уравнение u′x+u= f(u) или в более удобном виде u′ = f(u)–u. (2)

4). Уравнение (2) может иметь решение при условии: φ(u₀)= f(u₀)–u₀=0. Это даст решение в виде прямой линии: u=u₀ , или y=u₀ x.

5). Далее делением на выражение f(u)–u (учтем, что теперь f(u)–u ≠ 0) получаем уравнение с разделяющимися переменными: = .

6). Интегрируем уравнение (1): = lnCx.

7). Записываем ответ, учитывая что . Также учитываем полученные ранее в п.1) и в п.4) решения (если они оказались возможны!).

Решение–В: учтем, что самым простым решением задачи является решение, приводящее к уже отработанной схеме решения.

Общая схема решения уравнения f₁(x,y)dx+f₂(x,y)dy=0 такова:

1). Выделяем возможные решения исходного уравнения. Первое: f₁(x,y₀)=0. Это дает одно из решений: y=y₀ – прямая, параллельная оси ОХ. Второе: f₂(x₀,y)=0. Это дает ещё одно из решений: x=x ₀ – прямая, параллельная оси ОY.

2). Для уравнения: f₁(x,y)dx+f₂(x,y)dy = 0 запишем очевидное преобразование: y′= , где = , где правая часть является однородной функцией нулевого порядка, так как f₁(x,y) и f₂(x,y) – однородные функции одного порядка. Здесь учтено: f₂(x,y) ≠ 0.

3). После этого применяем схему Решения–А.

Замечание: формы А,В записи однородных уравнений будем называть стандартными.

§ 7. Уравнения специального вида, приводящиеся к однородному ду 1-го порядка

Рассмотрим еще один тип ДУ, приводимых к простейшим уравнениям с разделяющимися переменными.

Пусть уравнение задано в виде: y′= . Рассмотрим способы приведения таких уравнений к уравнениям с разделяющимися переменными. Возможны два случая.

Случай-1: определитель ≠0. Это значит, прямая l₁: a₁x+b₁y+c₁=0 и прямая l₂: a₂x+b₂y+c₂=0 пересекаются.

1). Применим преобразование переменных x и y : x=u+m; y=v+n, что определяет параллельный перенос системы координат XOY. Заметим: dx=du, dy=dv → y′= v′.

2). Получаем a₁x+b₁y+c₁= a₁u+b₁v+(a₁m+b₁n+c₁);

a₂x+b₂y+c₂= a₂u+b₂v+(a₂m+b₂n+c₂).

3). Выберем числа m и n , чтобы выполнялось: Это значит, что параллельный перенос производим в точку пересечения прямых и .

4). В результате получили уравнение: v′= =φ – однородное уравнение. После его интегрирования необходимо произвести замену переменных: и получить выражение решения заданного ДУ.

Случай-2: определитель =0. Это значит, прямая a₁x+b₁y+c₁=0 и прямая a₂x+b₂y+c₂=0 параллельны. В этом случае имеем: a₂=λa₁ и b₂=λb₁ и тогда = 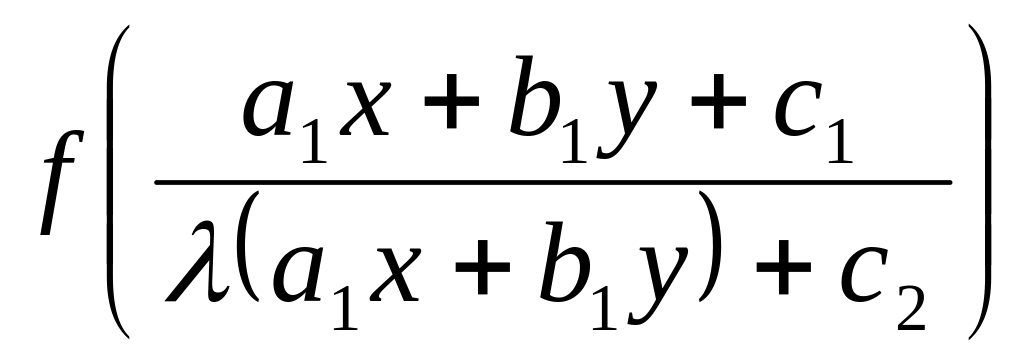= φ(a₁x+b₁y). Дальнейшее решение выполняется с использованием замены , что сразу приводит к уравнению с разделяющимися переменными.

Вопросы для самопроверки:

1. Какое уравнение называют дифференциальным?

2. Как определить порядок ДУ?

3. Что такое решение ДУ, частное решение ДУ?

4. Что такое общее решение ДУ?

5. Что значит решить Задачу Коши?

6. Что такое семейство кривых?

7. Как построить ДУ, решением которого является заданное семейство кривых?

8. Каковы стандартные формы ДУ с разделяющимися переменными?

9. Каковы стандартные формы однородных ДУ?

10. Какова стандартная схема решения ДУ с разделяющимися переменными?

11. Какова стандартная схема решения однородных ДУ?

12. Какова стандартная форма уравнений, приводящихся к однородным ДУ?

< * * * * * >