28

ДУ: Введение и Глава 1

Московский государственный институт электронной техники

(технический университет)

А. И. Литвинов

МЕТОДИЧЕСКОЕ ПОСОБИЕ

для самостоятельной работы студентов

по «Дифференциальным уравнениям»

Утверждено методическим советом каф. ВМ-2

Зав. кафедры С. Г. Кальней

МИЭТ, 2010 г.

—————————————————————————————————

Учиться, учиться и учиться!..

(Мудрость Гениев!)

Пособие соответствует утверждённому «Семестровому плану ЭТМО-1,2» и содержит систематизированный материал по «Дифференциальным уравнениям».

«Дифференциальные уравнения» (кратко ДУ) – это область знаний, в которой объединяются знания из математического анализа, алгебры и геометрии. Из математического анализа активно используется умение дифференцировать функции одной и нескольких переменных, вычислять интегралы (в первую очередь неопределённых). Из алгебры наиболее применяются разделы: тождественные преобразования, теория многочленов и линейная алгебра. Геометрия помогает «иллюстрировать» и исходные уравнения, и получаемые решения.

В пособии представлены общие теоретические сведения о дифференциальных уравнениях и методы интегрирования отдельных типов уравнений первого и высших порядков, а также систем дифференциальных уравнений. Большое внимание уделено задачам из геометрии, механики, физики и техники, требующим составления и решения дифференциальных уравнений.

Изложение материала пособия построено таким образом, чтобы оказать студентам максимальную помощь при выполнении текущих заданий, заданий БДЗ, а также при подготовке к зачётам и экзаменам.

Основные обозначения:

► и ◄ - начало и окончание доказательства.

☺☺ - поясняющие примеры.

Пример G–Х: - обозначение поясняющих примеров, где «G» указывает номер главы, в которой приводится пример, «Х» - порядковый номер поясняющего примера в главе.

☻ - окончание блока поясняющих примеров.

☺☻☺ - обобщающие примеры.

Пример N–Х: - обозначение обобщающих примеров, где «N» указывает порядковый номер примера в изучаемой главе, «Х» - номер задачи в базовом задачнике по изучаемому предмету.

☻ - окончание блока обобщающих примеров.

а A - элемент а принадлежит множеству A.

а A - элемент а не принадлежит множеству A.

N - множество натуральных чисел.

Z - множество целых чисел.

Q - множество рациональных чисел.

R - множество вещественных чисел.

C - множество комплексных чисел.

Буквы латинского алфавита

Начертание	Произношение	Начертание	Произношение	Начертание	Произношение
A a	а	J j	йот	S s	эс
B b	бэ	K k	ка	T t	тэ
C c	цэ	L l	эль	U u	у
D d	дэ	M m	эм	V v	вэ
E e	е	N n	эн	W w	дубль-вэ
F f	эф	O o	о	X x	икс
G g	же	P p	пэ	Y y	игрек
H h	аш	Q q	ку	Z z	зэт
I i	и	R r	эр

Буквы греческого алфавита

Начертание	Произношение	Начертание	Произношение	Начертание	Произношение
A α	альфа	I ι	йота	P ρ	ро
B β	бета	K κ	каппа	Σ σ	сигма
Г γ	гамма	Λ λ	ламбда	T τ	тау
Δ δ	дельта	M μ	ми	Υ υ	ипсилон
E ε	эпсилон	N ν	ни	Ф φ	фи
Z ζ	дзета	Ξ ξ	кси	X χ	хи
H η	эта	O ο	омикрон	Ψ ψ	пси
Θ θ	тэта	П π	пи	Ω ω	омега

Представлен наиболее употребительный (но не единственный) вариант произношения (в частности, вместо «же» говорят также «ге», вместо «жи» - «йот»).

СОДЕРЖАНИЕ:

Стр.

Глава 1. Общие сведения. Теорема о существовании и единственности решения ДУ 1-го порядка. Уравнения первого порядка с разделяющимися переменными.

§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

§ 2. Теорема о существовании и единственности решения ДУ 1-го порядка . . . . . . . . . . . . . . . . . . . . . 7

§ 3. Особые точки дифференциального уравнения 1-го порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

§ 4. Простейшие задачи, вытекающие из определения ДУ 1-го порядка . . . . . . . . . . . . . . . . . . . . . . . . . 11

§ 5. Уравнения 1-го порядка с разделяющимися переменными . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

§ 6. Применение уравнений с разделяющимися переменными: задачи из геометрии . . . . . . . . . . . . . . . 16

§ 7. Применение уравнений с разделяющимися переменными: задачи из физики . . . . . . . . . . . . . . . . . 18

§ 8. Обобщающие примеры по теме: «Уравнения с разделяющимися переменными» . . . . . . . . . . . . . . 21

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

Глава 2. Однородные функции и однородные уравнения первого порядка. Уравнения специального вида, приводящиеся к однородному ДУ 1-го порядка.

§ 1. Однородные функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

§ 2. Однородные уравнения первого порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

§ 3. Уравнения специального вида, приводящиеся к однородному ДУ 1-го порядка . . . . . . . . . . . . . . . 33

§ 4. Применение однородных уравнений: задачи из геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

§ 5. Применение однородных уравнений: задачи из физики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

§ 6. Обобщающие примеры по теме: «Однородные уравнения 1-го порядка» . . . . . . . . . . . . . . . . . . . . 37

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

Глава 3. Линейные дифференциальные уравнения 1-го порядка. Уравнения Бернулли.

§ 1. Линейные дифференциальные уравнения 1-го порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45

§ 2. Уравнения Бернулли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

§ 3. Применение линейных уравнений и уравнений Бернулли: задачи из геометрии . . . . . . . . . . . . . . 49

§ 4. Применение линейных уравнений и уравнений Бернулли: задачи из физики . . . . . . . . . . . . . . . . . 50

§ 5. Обобщающие примеры по теме: «Однородные уравнения 1-го порядка» . . . . . . . . . . . . . . . . . . . . 51

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

Глава 4. Дифференциальные уравнения в полных дифференциалах.

§ 1. Определение дифференциального уравнения в полных дифференциалах . . . . . . . . . . . . . . . . . . . . 58

§ 2. Способ решения ДУ в полных дифференциалах и общий алгоритм решения . . . . . . . . . . . . . . . . 59

§ 3. Использование интегрирующего множителя для получения ДУ в полных дифференциалах . . . 61

§ 4. Применение ДУ в полных дифференциалах: задачи из геометрии . . . . . . . . . . . . . . . . . . . . . . . . . 64

§ 5. Применение ДУ в полных дифференциалах: задачи из физики . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65

§ 6. Обобщающие примеры по теме: «ДУ в полных дифференциалах» . . . . . . . . . . . . . . . . . . . . . . . . . 66

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72

Глава 5. Уравнения первого порядка, не разрешенные относительно производной.

§ 1. Общие положения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

§ 2. Уравнения первого порядка n-й степени . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

§ 3. Уравнение, разрешённое относительно y и не содержащее x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74

§ 4. Уравнение, разрешённое относительно x и не содержащее y . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75

§ 5. Уравнение, не содержащее x или y, но разрешённое относительно y или x . . . . . . . . . . . . . . . . . . 75

§ 6. Уравнение Лагранжа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76

§ 7. Применение уравнений первого порядка, не разрешённых относительно производной:

задачи из геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

§ 8. Применение уравнений первого порядка, не разрешённых относительно производной:

задачи из физики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80

§ 9. Обобщающие примеры по теме: «Уравнения первого порядка, не разрешённые относительно

производной» . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

Глава 6. Семейство кривых линий. Огибающая семейства кривых. Особые решения дифференциального уравнения. Уравнение Клеро.

§ 1. Семейство кривых линий . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86

§ 2. Огибающая семейства кривых . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86

§ 3. Особые решения ДУ . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88

§ 4. Уравнение Клеро . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

§ 5. Применение уравнения Клеро: задачи из геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90

§ 6. Обобщающие примеры по теме: «Уравнение Клеро» . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . 91

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92

Глава 7. Уравнения высшего порядка. Уравнения, допускающие понижение порядка.

§ 1. Уравнения, допускающие понижение порядка . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93

§ 2. Обобщающие примеры по теме: «Уравнение допускающие понижение порядка» . . . . . . . . . . . . 96

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102

Глава 8. Линейные дифференциальные уравнения n-го порядка

§ 1. Общие сведения о линейных уравнениях n-го порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

§ 2. Некоторые теоремы о решениях линейного уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

§ 3. Линейная зависимость решений линейного уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104

§ 4. Линейные однородные уравнения с постоянными коэффициентами . . . . . . . . . . . . . . . . . . . . . . . 107

§ 5. Обобщающие примеры по теме: «Линейные ДУ n-го порядка» . . . . . . . . . . . . . . . . . . . . . . . . . . . 108

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

Глава 9. Линейные неоднородные дифференциальные уравнения n-го порядка

§ 1. Общие сведения о решениях линейного неоднородного уравнения . . . . . . . . . . . . . . . . . . . . . . . . 113

§ 2. Решение неоднородного ДУ методом «вариации произвольных постоянных» . . . . . . . . . . . . . . . 114

§ 3. Решение неоднородного ДУ методом «неопределенных множителей» . . . . . . . . . . . . . . . . . . . . . 115

§ 4. Обобщающие примеры по теме: «линейные неоднородные уравнения» . . . . . . . . . . . . . . . . . . . . 118

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125

Глава 10. Однородные и неоднородные уравнения Эйлера

§ 1. Однородное дифференциальное уравнение Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126

§ 2. Неоднородное дифференциальное уравнение Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128

§ 3. Краевые задачи для линейных ДУ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129

§ 4. Обобщающие примеры по теме: «уравнения Эйлера» . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132

Глава 11. Системы дифференциальных уравнений первого порядка

§ 1. Первичные сведения о системах дифференциальных уравнений первого порядка . . . . . . . . . . . 133

§ 2. Теорема о существование и единственности решения системы уравнений . . . . . . . . . . . . . . . . . 134

§ 3. Сведение системы ДУ к одному уравнению высшего порядка . . . . . . . . . . . . 134

§ 4. Механическая интерпретация системы уравнений 1-го порядка (фазовое пространство) . . . . . . 137

§ 5. Обобщающие примеры по теме: «Сведение системы ДУ к одному уравнению» . . . . . . . . . . . . 140

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143

Глава 12. Системы линейных однородных ДУ первого порядка с постоянными коэффициентами: частное и общее решения.

§ 1. Общие сведения о системе линейных однородных ДУ с постоянными коэффициентами . . . . . 144

§ 2. Частные решения системы линейных однородных ДУ с постоянными коэффициентами . . . . . . 144

§ 3. Общее и частное решения системы линейных однородных ДУ . . . . . . . . . . . . . . . . . . . . . . . . . . . 145

§ 4. Обобщающие примеры по теме: «Системы линейных однородных ДУ» . . . . . . . . . . . . . . . . . . . 155

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160

Глава 13. Системы линейных неоднородных ДУ 1-гого порядка с постоянными коэффициентами.

§ 1. Общие сведения о системе линейных неоднородных ДУ с постоянными коэффициентами . . . . 161

§ 2. Решение системы линейных неоднородных ДУ со специальной правой частью . . . . . . . . . . . . . 161

§ 3. Решение системы линейных неоднородных ДУ с произвольной правой частью . . . . . . . . . . . . . 168

§ 4. Обобщающие примеры по теме: «Системы линейных неоднородных ДУ» . . . . . . . . . . . . . . . . . 170

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176

Глава 14. Элементы теории устойчивости. Классификация точек покоя.

§ 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177

§ 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177

§ 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177

§ 4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177

§ 5. Обобщающие примеры по теме: «Устойчивость решений. Точки покоя» . . . . . . . . . . . . . . 177

Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177

Глава 1. Общие сведения. Теорема о существовании и единственности решения ду 1-го порядка. Уравнения первого порядка с разделяющимися переменными

С формальной точки зрения задачу решения дифференциального уравнения (кратко ДУ) можно рассматривать как задачу, обратную задаче дифференцирования.

Пусть имели функцию y=y(x) и определили её дифференциал: dy=y′(x)dx. Представим себе, что информация о функции y=y(x) утеряна и возникла необходимость её восстановить. Это и есть задача решения простейшего дифференциального уравнения. Символически её обозначают так: y = +C.

§ 1. Основные понятия

В математическом анализе для произвольной функции определены понятия дифференциалов и производных. Если дифференцирование заданной функции производится несколько раз, то устанавливаются понятия дифференциалов и производных высших порядков. Эти понятия при изучении ДУ являются базовыми. Заметим также, что в изучаемом курсе предполагается, что независимые переменные вещественные.

Определение: (1.1)

Дифференциальным уравнением называют равенство, содержащее независимые переменные, искомую функцию и её производные (или дифференциалы). Различают дифференциальные уравнения: 1) обыкновенные: функция зависит только от одной переменной; 2) в частных производных: функция зависит от нескольких переменных.

Замечание: 1). Мы будем изучать только обыкновенные ДУ.

2). Классификация форм записи ДУ использует в основном обозначения производных. При необходимости переход к форме «записи в дифференциалах» осуществляется по правилам математического анализа.

3). При решении обыкновенных ДУ первого порядка всегда предполагается «равноправие» переменных x и y: решение можно получить как в форме y=y(x), так и в форме x=x(y).

В общем случае дифференциальное уравнение можно записать в виде:

F(x, y, y′, y′′,… , y⁽ⁿ⁾) = 0, (1)

где y = y(x) – искомая функция независимой переменной x; y′, y′′,… , y⁽ⁿ⁾ – производные функции по x. Участие в записи ДУ производной y⁽ⁿ⁾ определяет порядок уравнения, а именно: n–й.

☺☺

Пример 1–01: Задано ДУ: y′′y⁽⁷⁾–y′x⁹= . Определить порядок этого уравнения.

Решение:

1). При определении порядка дифференциального уравнения учитывают принятые обозначения производной: y′, y′′,…, y^V, y⁽⁶⁾,…, y⁽ⁿ⁾.

2). В заданном уравнении «старшей» производной является y⁽⁸⁾. То, что эта производная находится под корнем, не имеет никакого значения!

3). Присутствие степени x⁹ не имеет отношения к обозначениям производной и не участвует в формировании порядка ДУ.

Ответ: порядок заданного уравнения n =8.

☻

В теории ДУ чаще всего используют запись:

y⁽ⁿ⁾ =f(x, y, y′, y′′,… , y^(n–1)), (2)

уравнение разрешено относительно старшей производной y⁽ⁿ⁾, такую запись называют нормальной формой записи. Уравнение называют линейным, если его форма записи:

y⁽ⁿ⁾) + a₁(x)y^(n–1) +… + a_n-1(x)y′ + a_ny =f(x), (3)

Совокупность уравнений:

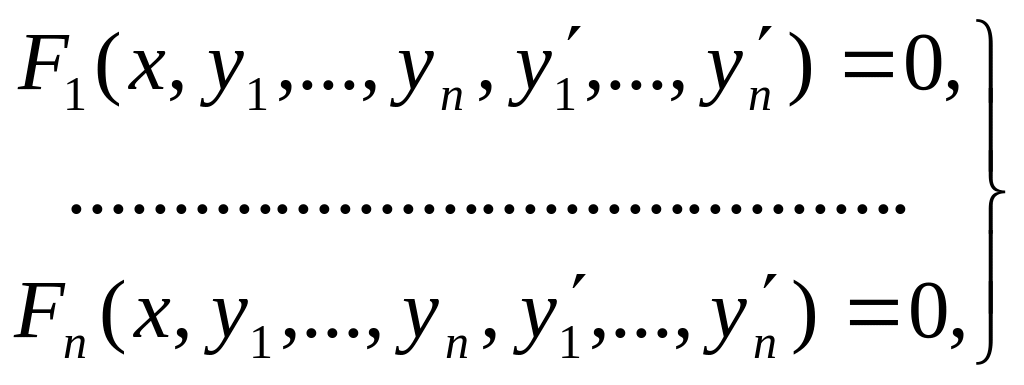(4)

где y₁,…,y_n – искомые функции от x, называется системой обыкновенных ДУ. Если эта система разрешена относительно производных от искомых функций, то её называют нормальной системой уравнений:

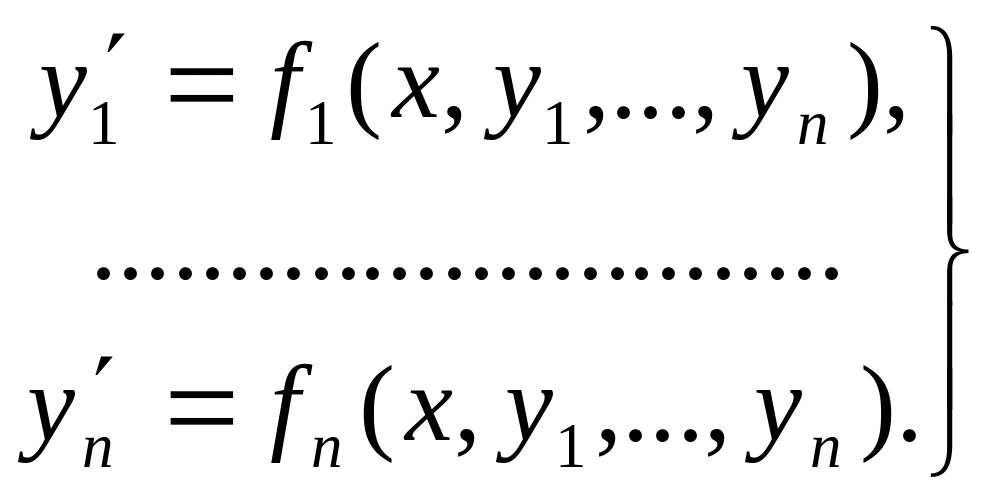(5)

Если нормальная система имеет вид:

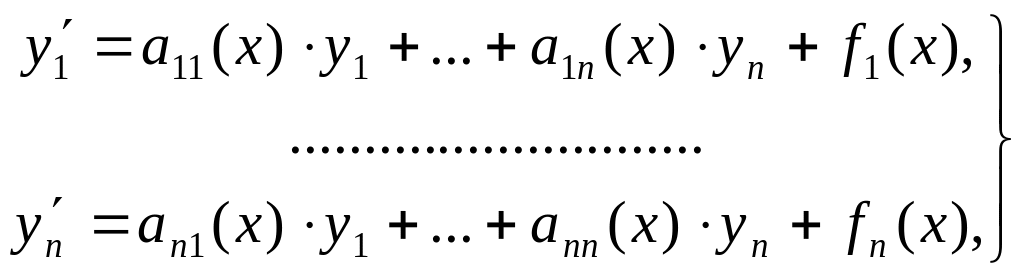(6)

то её называют линейной.

Пусть заданы дифференциальное уравнение (в любой из форм) и функция y=y(x). Что значит утверждение: функция y=y(x) является решением заданного ДУ?

Определение: (1.2)

Решением (интегралом) дифференциального уравнения называется всякая функция y=y(x), которая, будучи подставлена в заданное ДУ, превращает его в тождество.

Процесс нахождения решений ДУ называется интегрированием этого уравнения. Основная задача интегрирования ДУ: найти все решения уравнения и изучить их свойства.

Формы записи решений заданного ДУ могут различаться. Как правило, решения содержат произвольные постоянные. Роль этих постоянных будет уточняться при рассмотрении конкретных ДУ. Для нас в первую очередь важна роль произвольных постоянных в «Задаче Коши».

Пусть имеем ДУ: F(x,y,y′,y′′,…,y⁽ⁿ⁾)=0. Требуется найти решение уравнения y=y(x), которое удовлетворяет дополнительным условиям при заданном числовом значении x ₀:

y = y₀, y′ = , y′′ = ,… , y^(n–1) = . (7)

Такая задача называется Задачей Коши. Числа: x₀,y₀, , ,…, называют начальными условиями.

Рассмотрим реализацию задачи Коши на простейших уравнениях первого и второго порядков.

Пусть найдено решение ДУ 1-го порядка в форме: y=y(x,С), где С – произвольная постоянная. Геометрически это можно представить как семейство кривых на плоскости OXY, зависящее от одного параметра. Если через каждую точку плоскости проходит кривая семейства, то задача Коши означает выделение из семейства той кривой, которая проходит через точку (x₀,y₀). Алгебраически это означает решить уравнение: y₀=y(x₀,С), т.е. найти значение С, выделяющее «нужную» кривую. Следует: для решения задачи Коши в случае уравнения 1-го порядка полученное интегрированием решение должно содержать одну произвольную постоянную.

Пусть найдено решение ДУ 2-го порядка в форме: y=y(x,С₁,С₂), где С₁,С₂ – произвольные постоянные. Геометрически это можно представить как семейство кривых на плоскости OXY, зависящее от двух параметров. Если через каждую точку плоскости проходит кривая семейства, то задача Коши означает выделение из семейства той кривой, которая проходит через точку (x₀,y₀) и имеет заданный угловой коэффициент: . Алгебраически это означает решить систему уравнений: y₀=y(x₀,С₁,С₂) и =y′(x₀,С₁,С₂), т.е. найти значения С₁,С₂, выделяющие «нужную» кривую. Следует: для решения задачи Коши в случае уравнения 2-го порядка полученное интегрированием решение должно содержать две произвольные постоянные.

Обобщение: для решения задачи Коши в случае уравнения n-го порядка необходимо, чтобы решение содержало n произвольных постоянных.

При решении задачи Коши принципиальным моментом является определение произвольных постоянных, обеспечивающих выполнение начальных условий.

Определение: (1.3)

Общим решением дифференциального уравнения n-го порядка называют функцию y=y(x,С1,С2,…,Сn), которая зависит от n произвольных постоянных и удовлетворяет условиям: 1). Функция y=y(x,С1,С2,…,Сn) – решение ДУ при любых С1,С2,… , Сn; 2). Для начальных условий: y0, , ,…, в точке (x0,y0) можно определить все С1,С2,… , Сn , обеспечивающие выполнение начальных условий.

Из определения общего решения следует алгебраическая задача: имеется n уравнений с неизвестными величинами С₁,С₂,…,С_n. Необходимо определить эти неизвестные из системы уравнений:

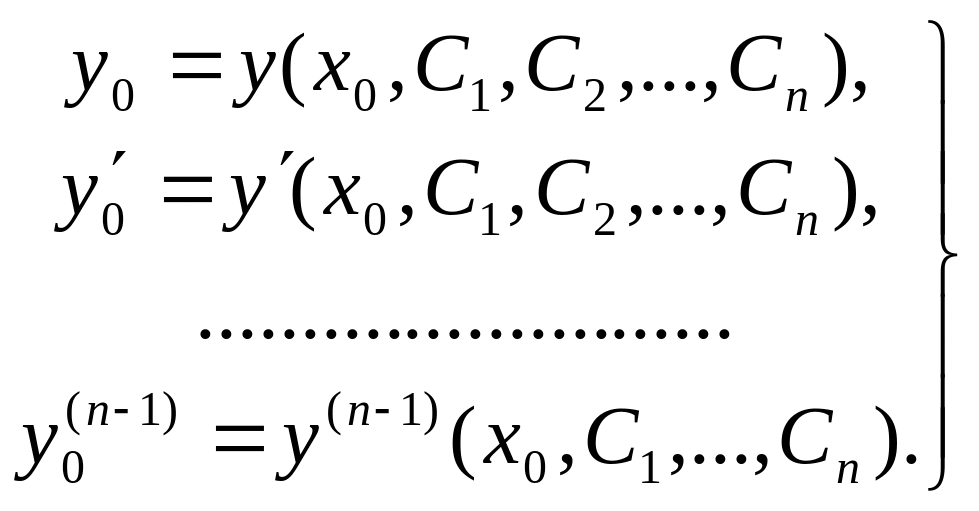(8)

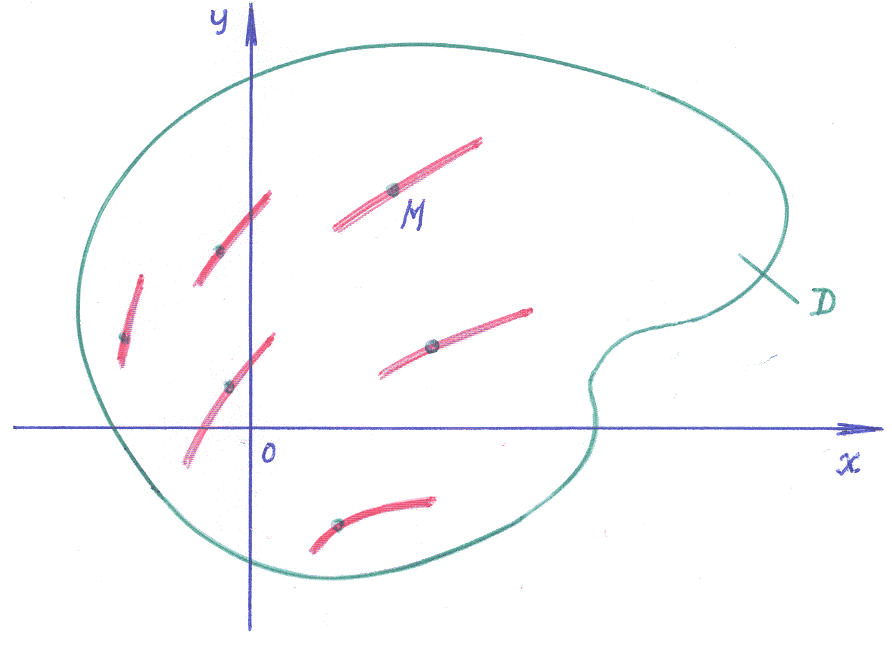Е сли заданное ДУ других решений, кроме решения y=y(x,С₁,С₂,…,С_n) , не имеет и система (8) имеет единственное решение при определении произвольных постоянных С₁,С₂,…,С_n, то мы «наблюдаем» реализацию «Теоремы о существовании и единственности решения заданного ДУ».

Замечание: При решении ДУ 1-го порядка получение решения ДУ в виде явной функции y=φ(x,С) следует рассматривать как самый простой случай, который не часто наблюдается. Учитывая возможности вычисления неопределенных интегралов, следует также иметь в виду, что «берущихся интегралов» совсем немного. Это значит, что получить аналитическое выражение решения чаще не удаётся. Мы будем считать, что ДУ решено даже в случае, если удалось просто расставить символы интегрирования! Все эти случаи объединим одним общим «выражением»:

Ф(x,y,С)=0 – общий интеграл (С – произвольная постоянная).

Имея определение «общего решения», определим понятие «частного» решения ДУ.

Определение: (1.4)

Частным решением дифференциального уравнения n-го порядка называется: 1). Функция y=y(x,С1,С2,… , Сn) решения ДУ при любых частных значениях постоянных С1,С2,… , Сn; 2). Любая функция, которая обращает ДУ в тождество.

Выражение Ф(x,y,С)=0 общего интеграла ДУ 1-го порядка при С=С₀ называют частным интегралом. Так как на плоскости OXY решение y=y(x,С) при любом значении С изображается кривой, то каждую их них называют интегральной кривой. То же говорят и в случае использования выражения Ф(x,y,С)=0.