
- •§ 5. Обобщающие примеры по теме: «Устойчивость решений. Точки покоя» . . . . . . . . . . . . . . 177
- •Глава 1. Общие сведения. Теорема о существовании и единственности решения ду 1-го порядка. Уравнения первого порядка с разделяющимися переменными
- •§ 1. Основные понятия
- •§ 2. Теорема о существовании и единственности решения ду 1-го порядка
- •§ 3. Особые точки дифференциального уравнения 1-го порядка
- •§ 4. Простейшие задачи, вытекающие из определения ду 1-го порядка
- •§ 5. Ду 1-го порядка с разделяющимися переменными
- •§ 6. Применение ду с разделяющимися переменными: задачи из геометрии
- •§ 7. Применение ду с разделяющимися переменными: задачи из физики
- •§ 8. Обобщающие примеры по теме: «ду с разделяющимися переменными»
§ 3. Особые точки дифференциального уравнения 1-го порядка
К особым точкам дифференциального уравнения F(x,y,y′)=0 относят точки, в которых нарушается либо «существование», либо «единственность» решения.
Заметим также, что условия теоремы 1.1 являются лишь достаточными, но не необходимыми. Поэтому особые точки ДУ следует искать среди точек разрыва функции f(x,y) и точек, где не существует производная , но не все такие точки обязательно особые!
Поведение интегральных кривых в окрестности особой точки бывает различным. Мы рассмотрим уравнение, особая точка которого очевидна – (0,0):
y′=![]() .
.
☺☺
Пример 1–06:
Для дифференциального уравнения: y′=![]() установить вид особой точки (0,0).
установить вид особой точки (0,0).
Решение:
1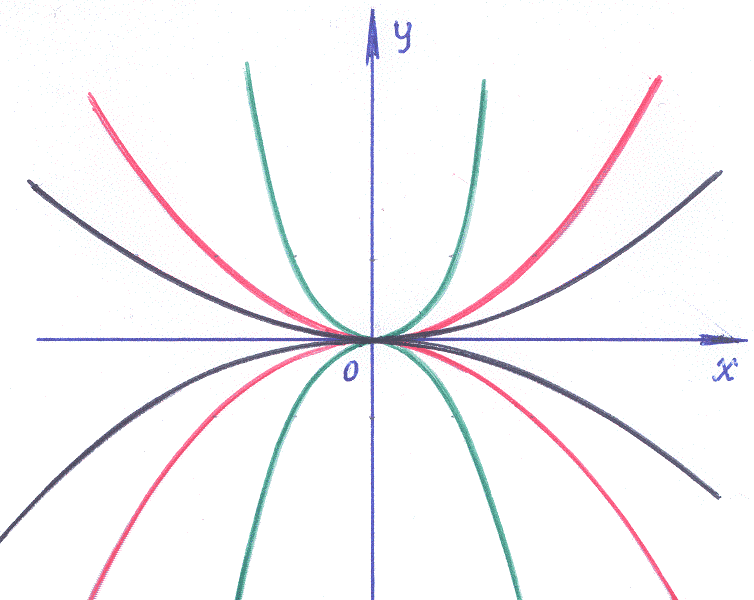 ).
Легко видеть, что в уравнении переменные
и легко разделяются:
).
Легко видеть, что в уравнении переменные
и легко разделяются:
![]() =2
=2![]() . (1)
. (1)
2). Общее решение уравнения (1): y=Сx2.
3). При любом C имеем параболу, содержащую точку (0,0), то есть в этой точке нарушена «единственность» решения → точка (0,0) – особая. Её называют «узлом»
Ответ: Особая точка заданного ДУ– «узел» (см. рисунок).
Пример 1–07:
Для дифференциального уравнения: y′=![]() установить вид особой точки (0,0).
установить вид особой точки (0,0).
Решение:
1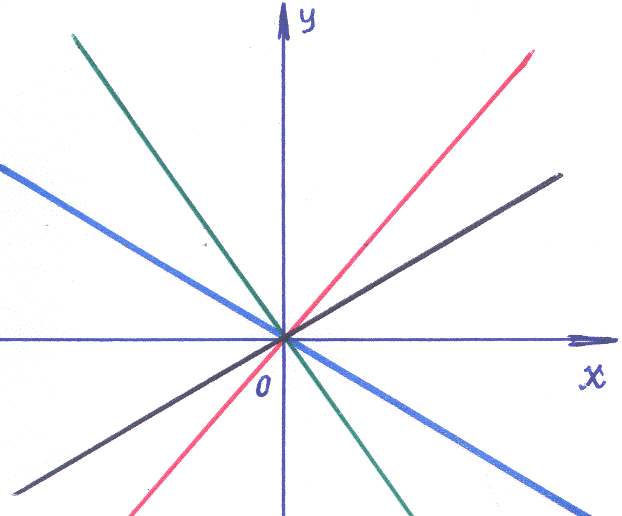 ).
Легко видеть, что в уравнении переменные
и легко разделяются:
=
. (1)
).
Легко видеть, что в уравнении переменные
и легко разделяются:
=
. (1)
2). Общее решение уравнения (1): y=Сx.
3). При любом C имеем прямую, содержащую точку (0,0), то есть в этой точке нарушена «единственность» решения → точка (0,0) – особая. Её называют «дикритическим узлом». Отличается от предыдущего тем, что в особой точке каждая интегральная кривая имеет своё направление.
Ответ: Особая точка заданного ДУ– «дикритический узел» (см. рисунок).
Пример 1–08: Для дифференциального уравнения: y′=– установить вид особой точки (0,0).
Решение:
1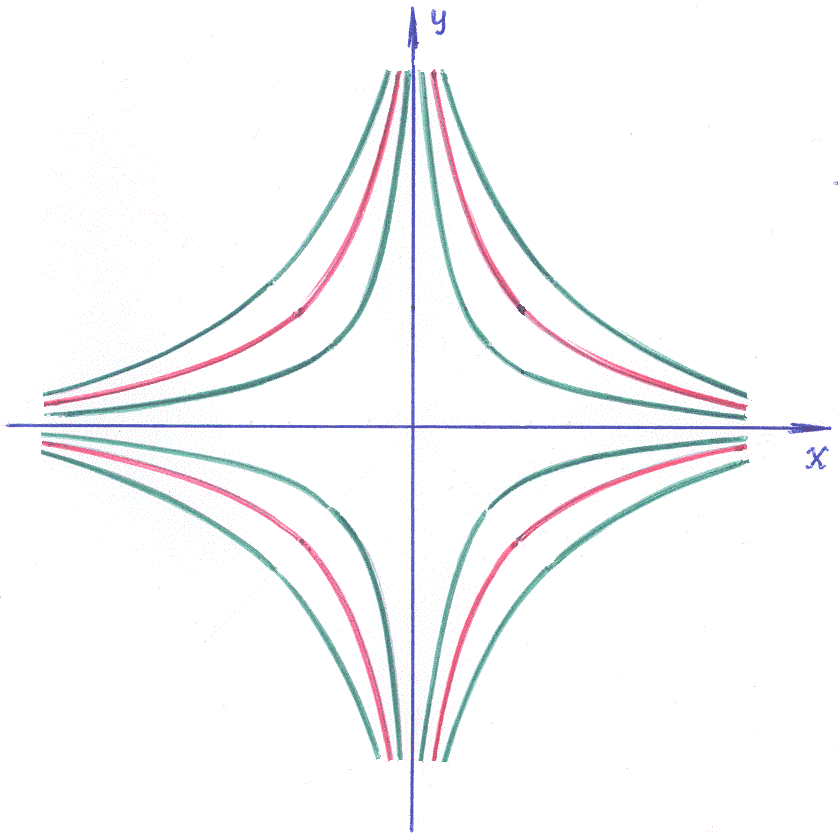 ).
Легко видеть, что в уравнении переменные
и легко разделяются:
=–
. (1)
).
Легко видеть, что в уравнении переменные
и легко разделяются:
=–
. (1)
2). Общее решение уравнения (1): xy=С – семейство гипербол.
3). При C=0 имеем оси координат: x=0, y=0. В точке (0,0) точке нарушена «единственность» решения → точка (0,0) – особая. Её называют «седловиной». Отличается от предыдущего тем, что при C≠0 интегральные кривые через особую точку не проходят.
Ответ: Особая точка заданного ДУ– «седловина» (см. рисунок).
Пример 1–09:
Для дифференциального уравнения: y′=![]() установить вид особой точки.
установить вид особой точки.
Решение:
1).
Легко видеть, что уравнение однородное:
xu′=![]() –u,
или xu′=
–u,
или xu′=![]() . (1)
. (1)
2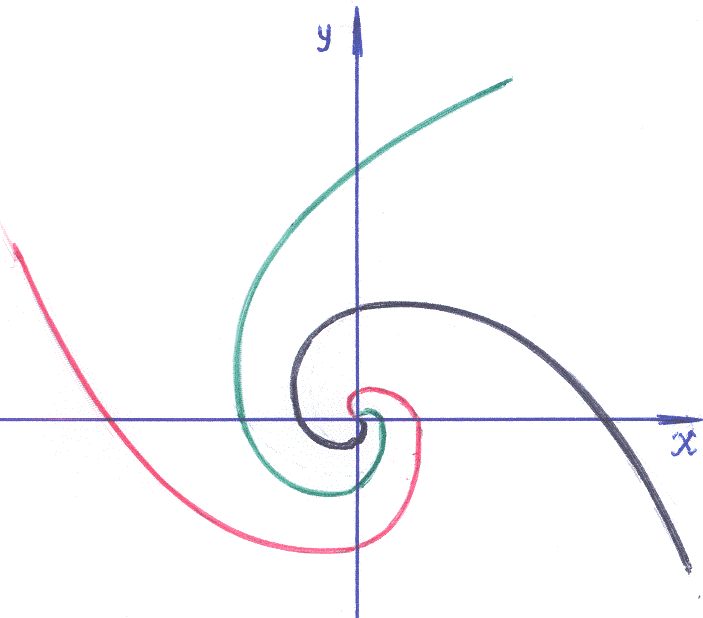 ).
Общее решение уравнения (1):
arctgu–
).
Общее решение уравнения (1):
arctgu–![]() ln(1+u2)=
lnСx,
или x
ln(1+u2)=
lnСx,
или x![]() =Сearctgu,
или
=Сearctgu,
или
![]() =
=![]() .
Перейдем к полярным координатам: ρ=Сeφ
– семейство логарифмических спиралей,
которые образуют вокруг начала координат
неограниченное число витков (при φ=–∞).
.
Перейдем к полярным координатам: ρ=Сeφ
– семейство логарифмических спиралей,
которые образуют вокруг начала координат
неограниченное число витков (при φ=–∞).
3). При C=0 имеем точку (0,0). В точке (0,0) нарушена «единственность» решения → точка (0,0) – особая. Её называют «фокусом». Отличается от предыдущего тем, что при C≠0 интегральные кривые через особую точку не проходят.
Ответ: Особая точка заданного ДУ– «фокус» (см. рисунок).
Пример 1–10:
Для дифференциального уравнения: y′=–![]() установить вид особой точки (0,0).
установить вид особой точки (0,0).
Решение:
1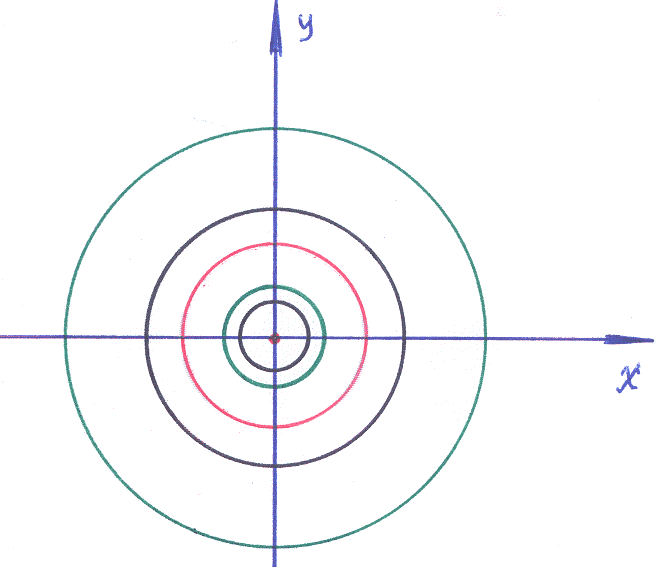 ).
Легко видеть, что в уравнении переменные
и легко разделяются: xdx+ydy=0. (1)
).
Легко видеть, что в уравнении переменные
и легко разделяются: xdx+ydy=0. (1)
2). Общее решение уравнения (1): x2+y2=С – семейство концентрических окружностей.
3). При C=0 имеем точку (0,0). Точка (0,0) не является решением так как исходное уравнение не существует в этой точке → точка (0,0) – особая. Её называют «центром». Отличается от предыдущего тем, что при C≠0 интегральные кривые через особую точку не проходят.
Ответ: Особая точка заданного ДУ– «центр» (см. рисунок).
☻
