- •§ 5. Обобщающие примеры по теме: «Устойчивость решений. Точки покоя» . . . . . . . . . . . . . . 177
- •Глава 1. Общие сведения. Теорема о существовании и единственности решения ду 1-го порядка. Уравнения первого порядка с разделяющимися переменными
- •§ 1. Основные понятия
- •§ 2. Теорема о существовании и единственности решения ду 1-го порядка
- •§ 3. Особые точки дифференциального уравнения 1-го порядка
- •§ 4. Простейшие задачи, вытекающие из определения ду 1-го порядка
- •§ 5. Ду 1-го порядка с разделяющимися переменными
- •§ 6. Применение ду с разделяющимися переменными: задачи из геометрии
- •§ 7. Применение ду с разделяющимися переменными: задачи из физики
- •§ 8. Обобщающие примеры по теме: «ду с разделяющимися переменными»
§ 2. Теорема о существовании и единственности решения ду 1-го порядка
Пусть имеем дифференциальное уравнение первого порядка: y′ = f(x,y). Для такого уравнения Теорема о существовании и единственности решения принимает вид:
Теорема: (1.1) |
Если
функция f(x,y)
есть непрерывная функция переменных
x,
y
в замкнутой области D:
|x–
x0|
≤
a;
|
y
–
y0|
≤
b,
где a,b
–
некоторые числа,
и ее частная производная
|
Замечания: 1). Графически указанная Теорема выглядит так: в области D через каждую точку М(x,y) проходит одна из интегральных кривых.
2). Установление существования и единственности решения для каждого заданного дифференциального уравнения – непростая задача! Мы будем рассматривать Теорему о существовании и единственности решения ДУ по мере изучения уравнений различных порядков и типов.
► Доказательство теоремы проведём «пошагово», последовательно используя заданные требования к свойствам функции f(x,y).
10. Так как функция f(x,y) непрерывна в замкнутой области D, то она в этой области ограничена, т.е. верно: | f(x,y)| ≤ M, где M постоянное положительное число.
Выберем
число: h=min![]() .
В теореме Пеано доказано, что в интервале
|x–
x0|
≤
h
уравнение y′
=
f(x,y)
имеет хотя
бы дно решение.
.
В теореме Пеано доказано, что в интервале
|x–
x0|
≤
h
уравнение y′
=
f(x,y)
имеет хотя
бы дно решение.
☺☺
Пример
1–02:
пусть имеем уравнение: y′
=2![]() .
В этом случае f(x,y)=
2
–
непрерывна в любой точке (x0,y0)
плоскости OXY, т.е. требование теоремы
Пеано выполняется. Легко проверить,
что функции:
.
В этом случае f(x,y)=
2
–
непрерывна в любой точке (x0,y0)
плоскости OXY, т.е. требование теоремы
Пеано выполняется. Легко проверить,
что функции:
y= |
|
y= |
|
y= |
|
являются решением заданного ДУ, т.е. теорема Пеано гарантирует существование решений ДУ, у которых выполняется условие: функция f(x,y) – непрерывна в замкнутой области D, но не обеспечивает единственности. |
|
☻
20.
Условие непрерывности
в
области D
также в этой области обеспечивает
ограниченность функции:
,
т.е. выполнение неравенства:
![]() ≤
К,
где К
постоянное положительное число. В
теореме Пика′ра доказано, что уравнение
y′
=
f(x,y)
имеет единственное решение, удовлетворяющее
заданным начальным условиям, в интервале
|x–
x0|
≤
h,
где h=min
.
≤
К,
где К
постоянное положительное число. В
теореме Пика′ра доказано, что уравнение
y′
=
f(x,y)
имеет единственное решение, удовлетворяющее
заданным начальным условиям, в интервале
|x–
x0|
≤
h,
где h=min
.
☺☺
Пример 1–03:
пусть имеем уравнение: y′
=2![]() ,
y≥0.
В этом случае
=
,
y≥0.
В этом случае
=
![]() –
существует и непрерывна при y
>0,
т.е. требование теоремы Пикара выполняется
в верхней полуплоскости OXY.
–
существует и непрерывна при y
>0,
т.е. требование теоремы Пикара выполняется
в верхней полуплоскости OXY.
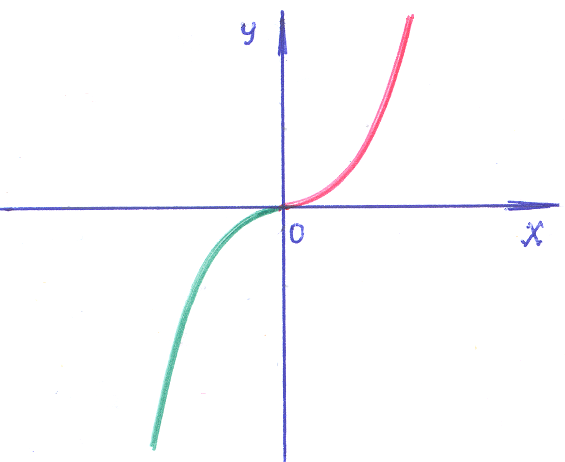
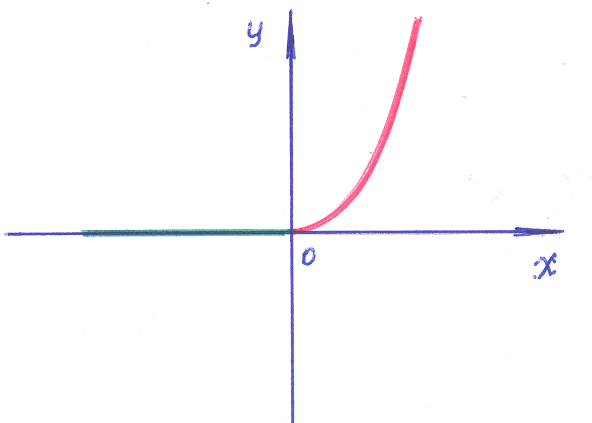
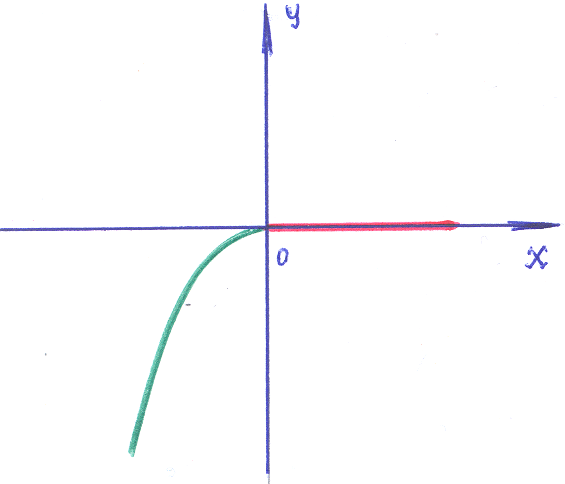
Легко проверить, что в области y≥0 «единственность» решения не обеспечивается. Теперь в точке (0,0) решений два: 1) y=0 – ось Х (зеленая); 2) x= – парабола (красная). В области y >0 решением в точке (0,0) будет только функция: x= – парабола (красная).
|
|
Замечание: на экзамене представленных в теореме «иллюстраций» достаточно, чтобы показать понимание сути условий Теоремы для уравнения вида: y′ = f(x,y). ◄
☻
Восприятию Теоремы 1.1 способствует использование понятий «поле направлений» и «изоклины». Воспользуемся дифференциальным уравнением в виде: y′=f(x,y).
Поле направлений: если выделена некоторая точка плоскости (x0,y0), то это определяет число = k0 = f(x0,y0). Учитывая, что геометрический смысл производной – угловой коэффициент касательной к кривой в выделенной точке, можем сказать, что уравнение y′=f(x, y) определяет «поле направлений» на плоскости OXY. Это поле можно сделать видимым в выделяемых точках, если в каждой точке построить коротенькую черточку.
☺☺
Пример 1–04: Задано ДУ: (2x+y2)dx–xdy=0. Определить, принадлежат ли точки: (1,0,2), (2,2,4), (1,1,2) полю направлений этого уравнения.
Решение:
1). Разделив исходное дифференциальное уравнение на dx, получим: (2x+y2)–xy′=0. Это соответствует общей записи ДУ 1-го порядка: F(x,y,y′)=0.
2). В полученное уравнение F(x,y,y′)=0 подставим «координаты точки» (x,y,y′) и произведем все алгебраические действия. В нашем случае применяем данные трех точек:
а). А(1,0,2) → (2∙1+02)– 1∙2=0 → точка А принадлежит полю направлений.
б). В(2,2,4) → (2∙2+22)– 2∙4=0 → точка В принадлежит полю направлений.
в). С(1,1,2) → (2∙1+12)– 1∙2≠0 → точка С не принадлежит полю направлений.
Ответ: точки А и В принадлежат полю направлений. Точка С не принадлежит полю направлений.
☻
Изоклины: линия, определяемая уравнением k0=f(x,y), называется изоклиной, так как в каждой её точке направление поля, определяемого уравнением y′=f(x,y), имеет постоянную величину k0. Использование изоклины для построения поля направлений бывает удобно, так как все «черточки» касательных на ней параллельны!
☺☺
Пример 1–05: Задано ДУ: (2x–y)dx–x2dy=0. Определить, являются ли линии: 2x–y=2x2, 2x–y=3x2, 2x–y=2x изоклинами этого уравнения.
Решение:
1). Разделив исходное дифференциальное уравнение на dx, перепишем его: (2x–y)=x2y′. Примем y′=k. Тогда получим выражение: (2x–y)=x2k. Это соответствует общей записи изоклины для заданного уравнения при условии, что k – параметр.
2). В таком случае нетрудно заметить:
а). Запись: 2x–y=2x2 → изоклина уравнения при k=2.
а). Запись: 2x–y=3x2 → изоклина уравнения при k=3.
а). Запись: 2x–y=2x → не является изоклиной уравнения: нет такого значения k, при котором из записи (2x–y)=x2k получилась бы запись: 2x–y=2x.
Ответ: линии: 2x–y=2x2, 2x–y=3x2 – изоклины. Линия: 2x–y=2x – не изоклина.
☻