§ 6. Применение ду с разделяющимися переменными: задачи из геометрии

Задачи из геометрии интересны тем, что они позволяют построить семейство кривых линий по совокупным свойствам этих линий. Так как рассматриваются ДУ 1-го порядка, то к этим свойствам относят соотношения величин (x,y,y′), определяющих отрезки: абсциссы, ординаты, параметры касательных и нормалей.

Следующий Пример устанавливает все основные соотношения, определяющие наиболее часто применяемые «отрезки», связанные с произвольной кривой.

☺☺

П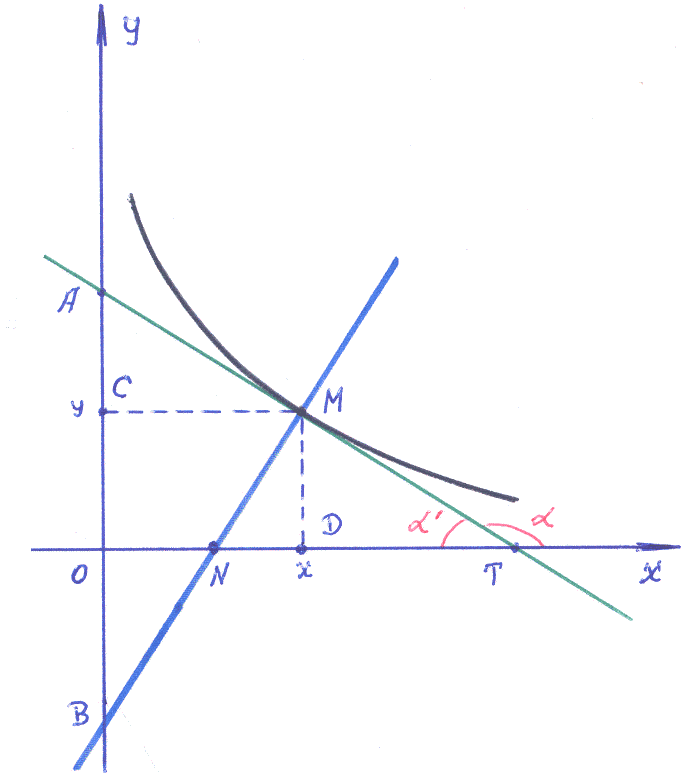 ример 1–19: Имеем уравнение кривой y=y(x). В точке М=(x,y) этой кривой проведены касательная и нормаль. Приняты понятия: (1)

▪ точка Т=(x_T,0) – точка пересечения касательной с ОХ;

▪ точка А=(0,y_А) – точка пересечения касательной с ОY;

▪ точка N=(x_N,0) – точка пересечения нормали с ОХ;

▪ точка B=(0,y_B) – точка пересечения нормали с ОY;

▪ точка D=(x,0) – абсцисса точки М;

▪ точка С=(0,y) – ордината точки М;

▪ отрезок МТ – отрезок касательной между точками М и Т;

▪ отрезок DТ – «подкасательная»: отрезок оси ОХ между точками D и Т;

▪ отрезок МN – отрезок нормали между точками М и N;

▪ отрезок DN – «поднормаль»: отрезок оси ОХ между точками D и N;

Определим координаты точек: Т,А ,N ,B , а также отрезки: МТ, DТ, МN, DN.

Решение:

1). Учитывая, что угловой коэффициент касательной равен y′, запишем уравнение касательной: y–y= y′(x –x), (1)

где (x,y) – произвольная точка касательной.

2). Учитывая, что угловой коэффициент нормали равен: – , запишем уравнение нормали: y–y= – (x –x), (2)

где (x,y) – произвольная точка нормали.

2). Определим координаты точек Т и А пересечения касательной (1) с осями координат:

а) y=0 → x=x_T =х– → T= ; б) x=0 → y=y_А= y–y′х → А=(0,y–y′х);

3). Определим координаты точек N и B пересечения нормали (2) с осями координат:

а) y=0 → x=x_N =х+yy′ → N=(х+yy′,0); б) x=0 → y=y_B=y+ → B=(0,y+ ).

4). Определим отрезок касательной и подкасательной:

а) вектор: МТ=Т–М= –(x,y)= ; б) длина: |МТ|= ;

в) вектор: DT=T–D= – ( х,0)= – подкасательная.

5). Определим отрезок нормали:

а) вектор: МN=N–М=(х+yy′,0)–(x,y)=(yy′,–y); б) длина: |МN|= .

в) вектор: ND=D–N=( х,0)– (х+yy′,0)= (–yy′,0) – поднормаль.

Ответ: Определены все упомянутые точки и отрезки.

Следствие: 1). Все точки определены как радиус-векторы. Отрезки определены сначала как «векторы», а потом как «длины».

2). Создавая из названных «элементов» различные равенства, будем получать дифференциальные уравнения, определяющие различные кривые!

Пример 1–20: Найти уравнение кривой, зная, что отрезок, который отсекается касательной в произвольной точке кривой на оси ординат, равен удвоенной ординате точки касания.

Р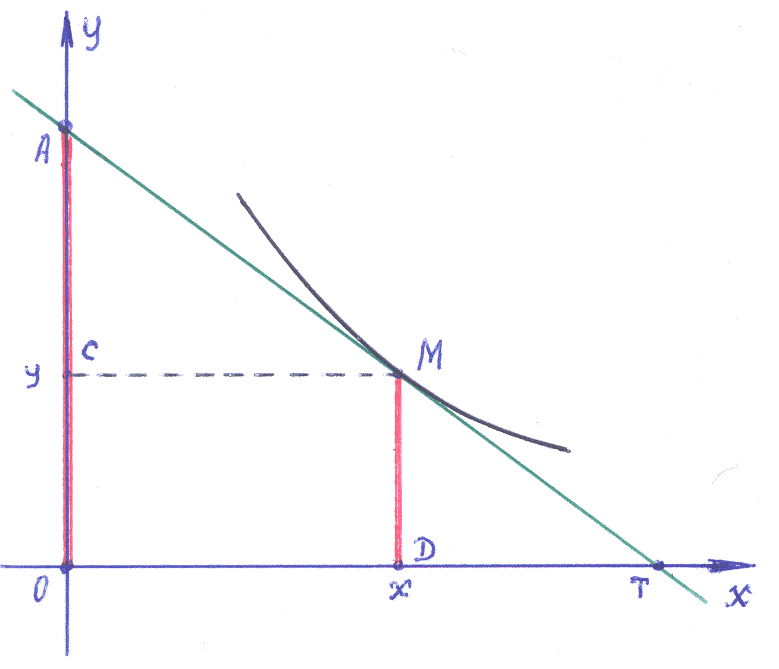 ешение:

В Примере 1–19 получены выражения: А=OА=(0,y–y′х); – отсекаемого касательной на оси ординат, DМ =(0,y) – ординаты.

Замечание: 1). В условии задачи допущена некорректность: если «отрезок» – «длина», то задача должна рассматриваться только для y >0;

2). Если условие задачи понимать в самом общем случае, то: |OА| = |DМ|.

Для лучшего восприятия задачи воспользуемся рисунком: отрезки ОА и МD выделены красным цветом. Через некоторую точку М(x,y) плоскости OXY проходит кривая y=(y) со свойством:

▪ Случай-1: [отрезок OА]= 2[отрезок DМ]; (1)

▪ Случай-2: [отрезок OА]= –2[отрезок DМ]. (2)

Случай-1.

0). Из условия запишем: y–y′х=2y, или хy′+y =0 – дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!

1). Запишем уравнение в виде: xdy + ydx =0 – уравнение с разделяющимися переменными.

2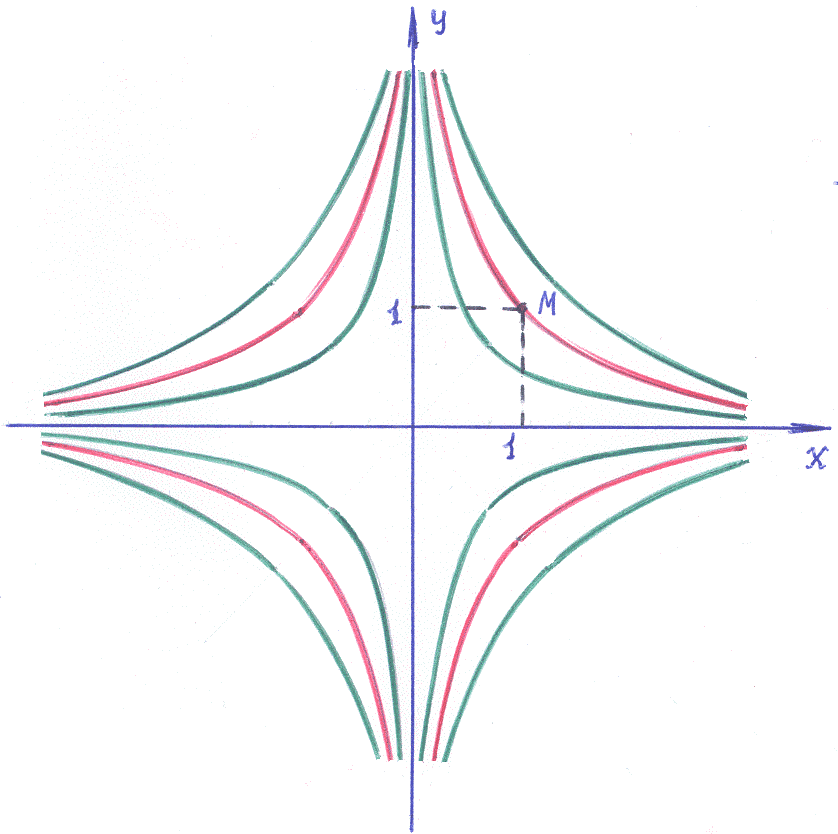 ). Учитывая Случай-В, запишем решения, которые следуют из исходной записи уравнения: x=0 – ось ОY; y=0 – ось ОХ. Эти решения не отражают существа поставленной «геометрической задачи».

3). Учитывая, что теперь x≠0 и y≠0, запишем уравнение в виде: + =0; «видим!»: переменные разделились → можно приступить к интегрированию ДУ!

4). Интегрируем: + =C или ln|y| + ln|x| = lnC, лучше: x∙y=C – общее решение дифференциального уравнения: семейство гипербол, известного из школы в виде записи: y=C .

Замечание: если потребовать, чтобы интегральная кривая проходила через точку М(1,1), то из семейства гипербол при С=1 была бы выделена гипербола: y= .

Случай-2.

0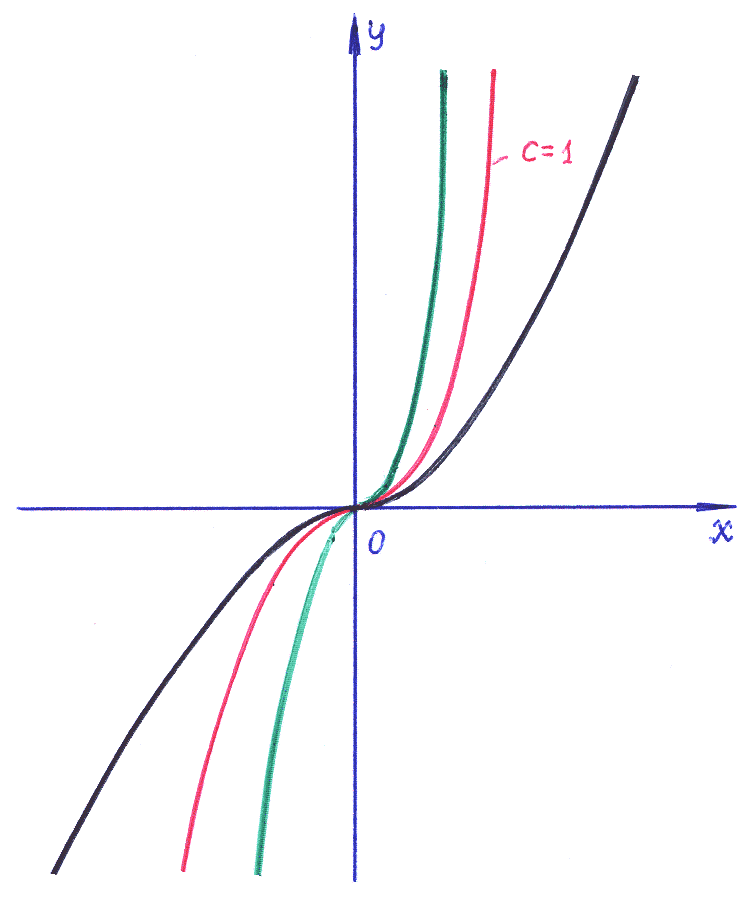 ). Из условия запишем: y–y′х=–2y, или хy′–3y=0 – дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!

1). Запишем уравнение в виде: xdy –3ydx =0 – уравнение с разделяющимися переменными.

2). Учитывая Случай-В, запишем решения, которые следуют из исходной записи уравнения: x=0 – ось ОY; y=0 – ось ОХ. Эти решения не отражают существа поставленной «геометрической задачи».

3). Учитывая, что теперь x≠0 и y≠0, запишем уравнение в виде: –3 =0; «видим!»: переменные разделились → можно приступить к интегрированию ДУ!

4). Интегрируем: =3 +C или ln|y|=3lnCx, лучше: y=Cx³ – общее решение дифференциального уравнения: семейство кубических парабол. На рисунке показаны интегральные кривые для С >0 (для лучшего восприятия!), для С<0 показанное семейство нужно зеркально отобразить относительно оси ОХ.

Ответ: Случай-1: y=C – общее решение ДУ; Случай-2: y=Cx³ – общее решение ДУ. Решения ДУ: x=0 и y=0 теряют привычный геометрический смысл, и мы их в этой задаче не выделяем!

☻