4). Это значит, что заданная функция является решением заданного ду.

Ответ: заданная функция является решением заданного ДУ.

Пример 2–5: В заданном семействе: y(1–Сх) =1 выделить уравнение кривой, удовлетворяющей приведенному начальному условию: y(1)=0.5.

Решение:

1). Выделить из семейства кривых кривую, которая проходит через точку (1; 0.5) – это значит вычислить значение С, при условии, что х=1; y =0.5.

2). Подставим х=0.5; y=1 в выражение семейства: 0.5∙(1–С∙1) =1, откуда C = –1.

3). Запишем выражение кривой семейства, проходящей через точку (1;0.5): y(1+х) =1.

Ответ: y(1+х) =1.

Пример 3–12: Составить дифференциальное уравнение семейства гипербол: x²– y² =2ax.

Решение:

1). Продифференцируем по х выражение заданного семейства: 2x– 2yy′ =2a и умножим его на x: 2x²– 2xyy′ =2ax.

2). Приравнивая левые части последнего равенства и семейства, получим: 2x²–2xyy′=x²–y² или 2xyy′=x²+y². Это и есть искомое ДУ.

Ответ: 2xyy′=x²+y².

Пример 4–18: Методом изоклин построить приближенно семейство интегральных кривых для дифференциального уравнения: y′= – .

Р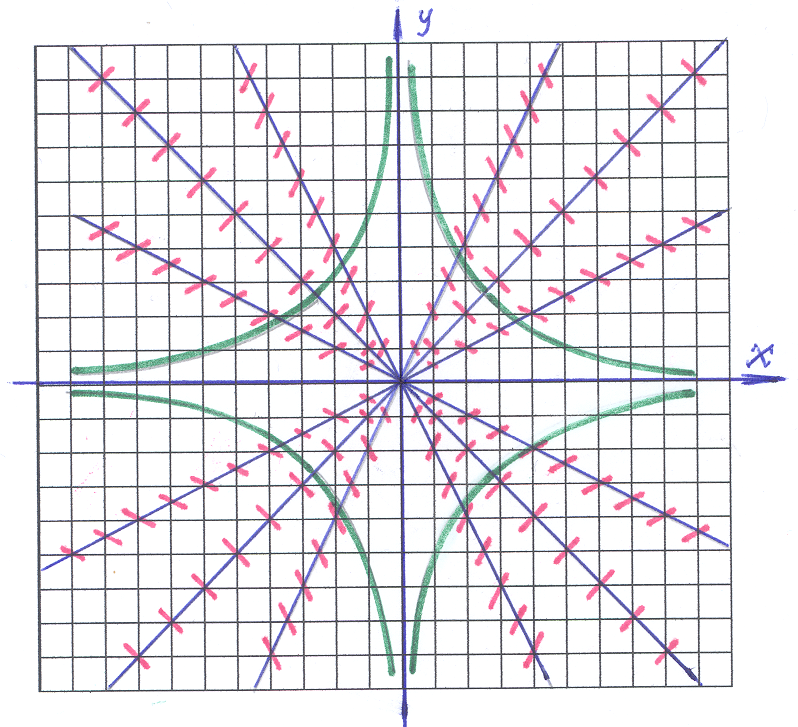 ешение:

1). Уравнение изоклин для заданного ДУ получается приравниванием y′=k. В нашем случае изоклина – прямая: y= –kx. На рисунке изоклины выделены «синим» цветом. На каждой изоклине черточка («красная») отражает конкретное значение k, определяющее изоклину, то есть: на каждой изоклине наклон черточки один и тот же.

2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемые «интегральные кривые» (на рисунке интегральные кривые выделены «зеленым» цветом), то есть «решение» заданного ДУ.

Ответ: интегральная кривая представлена на рисунке.

Пример 5–22: Решить дифференциальное уравнение: y′ = .

Решение:

0). Запишем уравнение в виде: ydy = xdx, «видим» – уравнение с разделяющимися переменными.

Замечание: раскрашивание «элементов» уравнения должно усилить восприятие образа «разделения переменных»: элементы одной переменной имеют один цвет, а второй – заметно отличающийся!

1). Учитывая «Решение–В», отметим, что из исходной записи уравнения ни одного решения не следует.

2). Интегрируем уравнение: = , или y² = x²+C – общее решение дифференциального уравнения.

Ответ: x² – y² = C – общее решение ДУ (семейство гипербол).

Пример 6–24: Решить дифференциальное уравнение: yy′ + x = 0.

Решение:

0). Запишем уравнение в виде: ydy + xdx =0, «видим» – уравнение с разделяющимися переменными.

1). Учитывая «Решение–В», отметим, что из исходной записи уравнения ни одного решения не следует.

2). Интегрируем уравнение: + = 0, или y² +x² = C – общее решение дифференциального уравнения.

Ответ: y² +x² = C – общее решение ДУ (семейство концентрических окружностей).

Пример 7–27: Решить дифференциальное уравнение: y′ = 1+ y².

Решение:

0). Запишем уравнение в виде: dy = (1+y²)dx – уравнение с разделяющимися переменными.

1). Учитывая «Решение–В», запишем решение, которое следует из исходной записи уравнения: x²–1=0, то есть х= ±1.

2). Учитывая, что теперь x²–1≠0, запишем уравнение в виде: = ; «видим!»: переменные разделились и можно приступить к интегрированию ДУ!

3). = или arctgy = arcsinx + C – общее решение дифференциального уравнения.

Ответ: arctgy = arcsinx + C – общее решение ДУ, также x=±1 (из общего решения не получается ни при каком значении С).

Пример 8–28: Решить дифференциальное уравнение: y′ = e^x+y.

Решение:

0). Запишем уравнение в виде: e^–ydy=e^xdx, «видим» – переменные разделились.

1). Учитывая «Решение–В», отметим, что из исходной записи уравнения ни одного решения не следует.

2). Интегрируем уравнение: = или e^x +e^–y = C – общее решение дифференциального уравнения.

Ответ: e^x +e^–y = C – общее решение ДУ.

Пример 9–29: Решить дифференциальное уравнение: y′ + = 0.

Решение:

0). Запишем уравнение в виде: y∙cosydy + x∙sinxdx = 0, «видим» – переменные разделились.

1). Учитывая «Решение–В», отметим, что из исходной записи уравнения ни одного решения не следует.

2). Интегрируем уравнение: + =C. Учтем: =[интегрирование по частям!]= =y∙siny+cosy; = –x∙cosx+sinx; тогда: y∙siny+cosy –x∙cosx+sinx = C – общее решение дифференциального уравнения.

Ответ: y∙siny+cosy –x∙cosx+sinx = C – общее решение ДУ.

Пример 10–32: Решить дифференциальное уравнение: ye^2x dx – (1+e^2x) dy = 0.

Решение:

0). Запишем уравнение в виде: ye^2xdx – (1+e^2x) dy = 0, «видим» – уравнение с разделяющимися переменными..

1). Учитывая «Решение–В», запишем решение, которое следует из исходной записи уравнения: y=0.

2). Учитывая, что теперь y≠0, запишем уравнение в виде: = ; «видим!»: переменные разделились → можно приступить к интегрированию ДУ!

3). Интегрируем: = или 2ln|y| = ln(1+e^2x) + lnC – общее решение дифференциального уравнения, или (лучше!) y² = С(1+e^2x).

Ответ: y² = С(1+e^2x) – общее решение ДУ, также: y = 0 (выделяется из общего при С=0).

Замечание: Выражение для общего решения, а также то, что решение y=0 выделяется из общего при С=0, свидетельствует о единственности решения задачи Коши в «доступных» точках плоскости!

Пример 11–45: Найти частное решение ДУ: y′tgx = y, удовлетворяющее условию: =1.

Решение:

0). Запишем уравнение в виде: dytgx = ydx, «видим» – уравнение с разделяющимися переменными..

1). Учитывая «Решение–В», запишем решения, которые следуют из исходной записи уравнения: tgх= 0, то есть х= πn, n Z (семейство прямых, параллельных оси OY) и y=0.

2). Учитывая, что теперь х≠πn и y≠0, запишем уравнение в виде: = ; «видим!»:: переменные разделились → можно приступить к интегрированию ДУ!

3). Интегрируем: n|y| = ln|sinx| + lnC – общее решение ДУ; лучше: y=Csinx.

4). Найдем частное решение для =1: 1=C sin → С=1. Частное решение: y=sinx.

Ответ: y = sinx – частное решение ДУ. Через точку проходит единственная интегральная кривая.

Пример 12–166: Найти уравнение кривой, проходящей через точке (1,2), если её подкасательная вдвое больше абсциссы точки касания.

Решение:

В Примере 1–18 получены выражения: DТ=Т–D= –(x,0)= ; – отсекаемого касательной на оси ординат, D=OD=(x,0) – ординаты.

Замечание: Условие задачи предполагает равенство величин: |DТ|=|OD|

Для лучшего восприятия задачи воспользуемся рисунком: отрезки ОD и DT выделены красным цветом. Через некоторую точку М(x,y) плоскости OXY проходит кривая y=(y) со свойством:

▪ Случай-1: [отрезок DТ]= 2OD; (1)

▪ Случай-2: [отрезок DТ]= –2OD. (2)

Случай-1.

0). Из условия запишем: =2x – дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!

1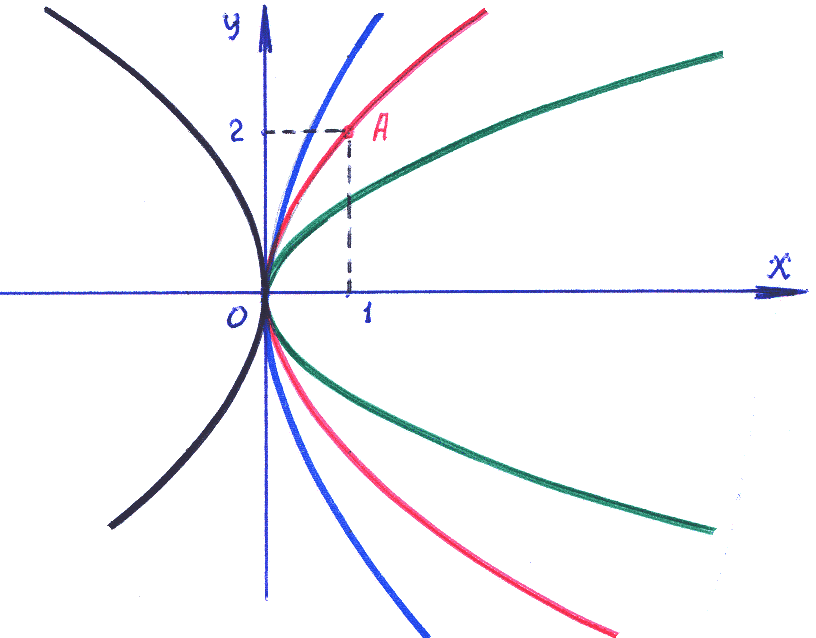 ). Запишем уравнение в виде: 2xdy = ydx – уравнение с разделяющимися переменными.

2). Учитывая «Решение–В», запишем решения, которые следуют из исходной записи уравнения: x=0 – ось ОY; y=0 – ось ОХ. Эти решения не отражают существа поставленной «геометрической задачи».

3). Учитывая, что теперь x≠0, и y≠0, запишем уравнение в виде: 2 = ; «видим!»: переменные разделились → можно приступить к интегрированию ДУ!

4). Интегрируем: 2 +C= или lnCy²=ln|x|, лучше: y²=Cx – общее решение дифференциального уравнения: семейство парабол.

Замечание: Если на плоскости XOY изобразить простейшую параболу: x=y² (назовем её «базовой»), то семейство кривых x=Сy² получают применением преобразований:

а) для С>0 : ▪ кривые заполняют правую полуплоскость; ▪ базовая кривая деформируется (сжать-растянуть) в С раз вдоль оси OX;

б) для С<0 : ▪ зеркально отобразить всё семейство кривых, полученных для С>0.

5). Интегральная кривая, проходящая через точку А=(1,2): y²=4x– частное решение дифференциального уравнения при С=4 (см. рисунок: выделено красным цветом).

Случай-2.

0). Из условия запишем: =2x – дифференциальное уравнение для нахождения кривой с заданными свойствами. Остается решить это уравнение!

1). Запишем уравнение в виде: 2xdy + ydx =0 – уравнение с разделяющимися переменными.

2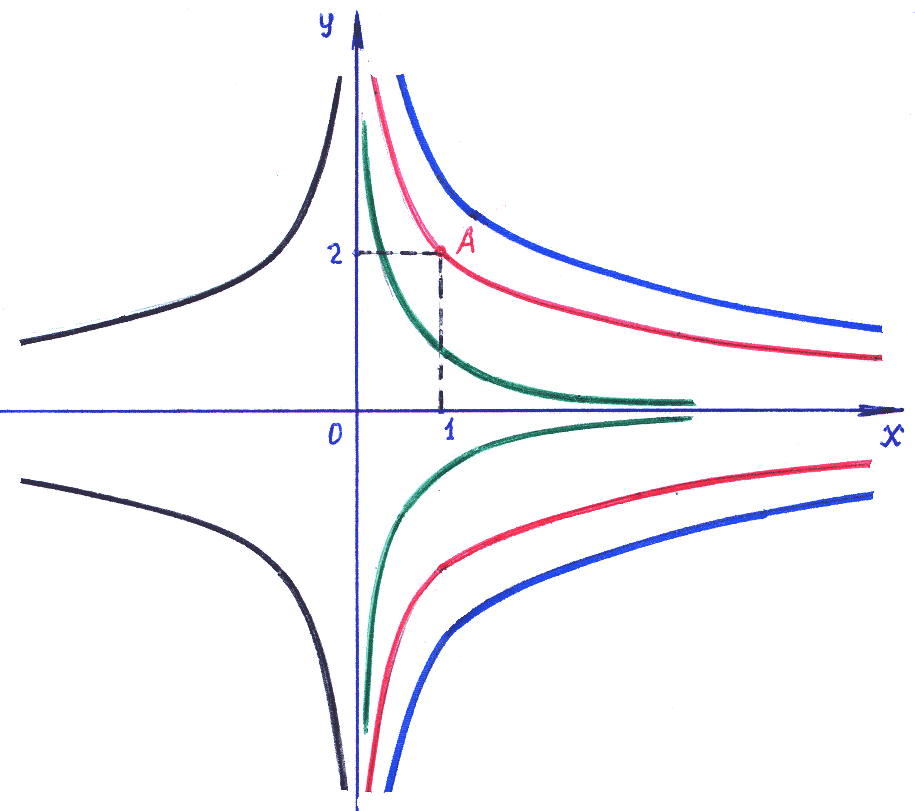 ). Учитывая «Решение–В», запишем решения, которые следуют из исходной записи уравнения: x=0 – ось ОY; y=0 – ось ОХ. Эти решения не отражают существа поставленной «геометрической задачи».

3). Учитывая, что теперь x≠0, и y≠0, запишем уравнение в виде: 2 + =0; «видим!»: переменные разделились → можно приступить к интегрированию ДУ!

4). Интегрируем: 2 + =C или lny²x=lnC, лучше: xy²=C – общее решение дифференциального уравнения: семейство кривых «гиперболического вида».

Замечание: Если на плоскости XOY изобразить простейшую «гиперболу»: x= (назовем её «базовой»), то семейство кривых x=С получают применением преобразований:

а) для С>0 : ▪ кривые заполняют правую полуплоскость; ▪ базовая кривая деформируется (сжать-растянуть) в С раз;

б) для С<0 : ▪ зеркально отобразить всё семейство кривых, полученных для С>0.

5). Интегральная кривая, проходящая через точку А=(1,2): y²=4x– частное решение дифференциального уравнения при С=4 (см. рисунок: выделено красным цветом).

Ответ: Случай-1: y=С – общее решение ДУ. Случай-2: x=4 – общее решение ДУ. Решения ДУ: x=0 и y=0 теряют привычный геометрический смысл, и мы их в этой задаче не выделяем!

☻

Вопросы для самопроверки:

1. Какое уравнение называют дифференциальным?

2. Как определить порядок ДУ?

3. Что такое решение ДУ, частное решение ДУ?

4. Что такое общее решение ДУ?

5. Что значит решить Задачу Коши?

6. Что такое семейство кривых?

7. Как построить ДУ, решением которого является заданное семейство кривых?

8. Каковы стандартные формы ДУ с разделяющимися переменными?

9. Какова стандартная схема решения ДУ с разделяющимися переменными?

< * * * * * >