
- •Занятие 1. Основные понятия. Теорема о существовании и единственности решения ду 1-го порядка. Уравнения первого порядка с разделяющимися переменными.
- •4). Это значит, что заданная функция является решением заданного ду.
- •Замечание: раскрашивание «элементов» уравнения должно усилить восприятие образа «разделения переменных»: элементы одной переменной имеют один цвет, а второй – заметно отличающийся!
- •4). Это значит, что заданная функция является решением заданного ду.
- •Замечание: раскрашивание «элементов» уравнения должно усилить восприятие образа «разделения переменных»: элементы одной переменной имеют один цвет, а второй – заметно отличающийся!
Замечание: раскрашивание «элементов» уравнения должно усилить восприятие образа «разделения переменных»: элементы одной переменной имеют один цвет, а второй – заметно отличающийся!
1). Учитывая «Решение–В», отметим, что из исходной записи уравнения ни одного решения не следует.
2).
Интегрируем уравнение:
![]() =
=![]() или
или
![]() =
x–
=
x–![]() +C,
лучше: y3=3x–x3+C
–
общее решение дифференциального
уравнения.
+C,
лучше: y3=3x–x3+C
–
общее решение дифференциального
уравнения.
Ответ: y3=3x–x3+C – общее решение ДУ.
Пример 9–25: Решить дифференциальное уравнение: xy′ =2y.
Решение:
0). Запишем уравнение в виде: xdy = 2ydx – уравнение с разделяющимися переменными.
1). Учитывая «Решение–В», запишем решения, которые следуют из исходной записи уравнения: x=0 и y=0.
2).
Учитывая, что теперь x≠0
и y≠0,
запишем уравнение в виде:
![]() =2
=2![]() ;
«видим!»: переменные разделились и можно
приступить к интегрированию ДУ!
;
«видим!»: переменные разделились и можно
приступить к интегрированию ДУ!
3).
Интегрируем:
![]() =2
=2![]() или ln|y|=2ln|x|+lnC,
лучше: y=Cx2
–
общее решение дифференциального
уравнения.
или ln|y|=2ln|x|+lnC,
лучше: y=Cx2
–
общее решение дифференциального
уравнения.
Ответ: y = Cx2 – общее решение ДУ, также x=0 (из общего решения не получается ни при каком значении С) и y=0 (входит в общее решение при С=0).
Пример 10–26: Решить дифференциальное уравнение: (x+1)y′+xy =0.
Решение:
0). Запишем уравнение в виде: (x+1)dy + xydx =0 – уравнение с разделяющимися переменными.
1). Учитывая «Решение–В», запишем решения, которые следуют из исходной записи уравнения: x+1=0 и y=0.
2).
Учитывая, что теперь x+1≠0
и y≠0,
запишем уравнение в виде:
+![]() =0;
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
=0;
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
3).
Интегрируем:
+![]() =C
или ln|y|
+ x
–
ln|x+1|
= C,
лучше:
=C
или ln|y|
+ x
–
ln|x+1|
= C,
лучше:
![]() =
eC–x=Ce–x
–
общее решение дифференциального
уравнения; еще лучше: y=C(x+1)e–x.
=
eC–x=Ce–x
–
общее решение дифференциального
уравнения; еще лучше: y=C(x+1)e–x.
Замечание: постоянная С «берет на себя» заботу о согласовании знаков величин, если будет необходимо учесть начальные условия!
3). Из общего решения ДУ при С=0 следует: решение y = 0, но ни при каком значении С не следует: x+1=0.
Ответ: y = С(x+1)e–x – общее решение ДУ; также x+1=0 (из общего решения не получается ни при каком значении С) и y=0 (входит в общее решение при С=0).
Пример 11–30: Решить дифференциальное уравнение: (1+y2)xdx +(1+x2)dy =0.
Решение:
0). «Раскрасим» заданное уравнение: (1+y2)xdx +(1+x2)dy =0 – уравнение с разделяющимися переменными.
1). Учитывая «Решение–В», отметим, что из исходной записи уравнения ни одного решения не следует.
2).
Запишем уравнение в виде: 2![]() +2
+2![]() =0
(умножение
на число 2 удобно!);
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
=0
(умножение
на число 2 удобно!);
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
2). Интегрируем: ln(1+ x2)+2arctgy =C – общее решение ДУ.
Ответ: ln(1+ x2)+arctgy =C – общее решение ДУ.
Пример 12–31:
Решить дифференциальное уравнение:
xydx
+![]() dy
=0.
dy
=0.
Решение:
1). Учитывая «Решение–В», запишем решения, которые следуют из исходной записи уравнения: x2–1=0, то есть х= ±1, и y=0.
2).
Учитывая, что теперь x2–1≠0
и y≠0,
запишем уравнение в виде:
![]() +
=0;
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
+
=0;
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
3).
Интегрируем: ln|y|
=
–lnC
–
общее решение ДУ; лучше: Сy=![]() или
y=С
.
или
y=С
.
4). Видим, что решение y = 0 можно получить из общего при С=0. Решение x= ±1 из общего решения не получается ни при каком значении С!
Ответ: y = С – общее решение ДУ; также решение: y = 0 (выделяется из общего при С=0) и x= ±1.
Пример 13–38:
Решить дифференциальное уравнение:
y′=![]() .
.
Решение:
0). Будем считать, что x=x(y). Перепишем заданное уравнение в виде: x′=y+2x или в общем виде: x′=f(ay+bx+c). Полученное уравнение имеет «Решение–С».
1). Запишем уравнение в виде: 2x′=2(y+2x)=2f(ay+bx+c).
2). Примем u=y+2x и запишем уравнение: u′=bf(u)+a=2u+1, или du=(2u+1)dy, что является уравнением с разделяющимися переменными.
3). Далее применяем «Решение–В»: получаем решение 2u+1=0, или 2y+4x+1=0.
4).
Учитывая, что теперь 2u+1≠0,
запишем уравнение в виде:
![]() =
dy,
или
=
dy,
или
![]() =2dy.
=2dy.
5).
Интегрируем уравнение по последней
записи: ln|2u+1|=2y+C
–
общее решение ДУ; лучше: 2u+1=![]() или
2u+1=С
или
2u+1=С![]() .
.
6). Учитывая: u=y+2x, получим окончательно: 4x+2y+1= С .
Ответ: 4x+2y+1= С – общее решение ДУ; решение 2y+4x+1=0 выделяется из общего при значении С=0.
Пример 14–41: Решить дифференциальное уравнение: y′+2y =3x+5.
Решение:
0). Преобразуем заданное уравнение: y′=3x–2y+5=f(ax+by+c). Полученное уравнение имеет «Решение–С».
1). Запишем уравнение в виде: –2y′=–2(3x–2y+5), из общего: by′ =bf(ax+by+c).
2). Примем u=3x–2y+5 и запишем уравнение: u′=bf(u)+a=–2u+3, или du=(–2u+3)dх, что является уравнением с разделяющимися переменными.
3). Далее применяем «Решение–В»: получаем решение –2u+3=0, или 2u–3=0, или через исходные переменные: 6x–4y+7=0.
4).
Учитывая, что теперь –2u+3≠0,
запишем уравнение в виде:
![]() =–dх,
или (лучше!)
=–dх,
или (лучше!)
![]() =–2dх.
=–2dх.
5).
Интегрируем уравнение по последней
записи: ln|2u–3|=–2х+C
–
общее решение ДУ; лучше: 2u–3=![]() или
2u–3=С
или
2u–3=С![]() .
.
6). Учитывая: u=3x–2y+5, получим окончательно: 6x–4y+7= С .
Ответ: 6x–4y+7= С – общее решение ДУ; решение 6x–4y+7=0 выделяется из общего при значении С=0.
Пример 15–43: Решить дифференциальное уравнение: (1+y2)dx –xydy =0, y(1)=0.
Решение:
0). «Раскрасим» заданное уравнение: (1+y2) dx – xydy =0 – уравнение с разделяющимися переменными.
1). Далее применяем «Решение–В»: получаем решение x=0.
2).
Учитывая, что теперь x≠0,
запишем уравнение в виде: 2![]() –2
–2![]() =0
(умножение на число 2 удобно!);
переменные разделились → можно
приступить к интегрированию ДУ!
=0
(умножение на число 2 удобно!);
переменные разделились → можно
приступить к интегрированию ДУ!
3). Интегрируем: lnx2–ln(y2+1)=C, лучше: y2+1=Cx2 – общее решение ДУ.
4). Используя начальные условия, вычисляем: С=1 → частное решение: x2–y2 =1– гипербола. График полученного уравнения имеет две ветви. Начальные условия выделяют правую ветвь гиперболы!
Ответ: x2–y2 =1 – частное решение ДУ: правая ветвь гиперболы.
Пример 16–167:
Найти
уравнение кривой, проходящей через
точке
![]() ,
если длина отрезка полуоси абсцисс,
отсекаемого её касательной, равна
квадрату абсциссы точки касания.
,
если длина отрезка полуоси абсцисс,
отсекаемого её касательной, равна
квадрату абсциссы точки касания.
Решение:
В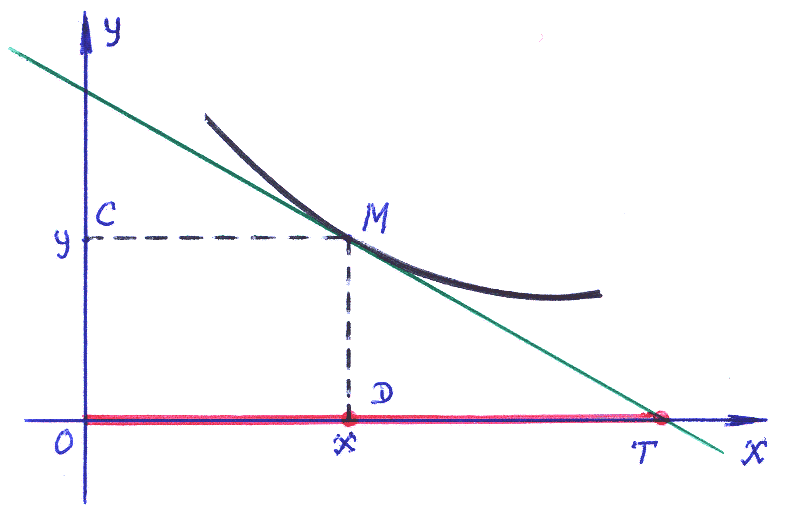 Примере
1–18
получены выражения:
Т=OТ=
Примере
1–18
получены выражения:
Т=OТ=![]() ;
– отсекаемого
касательной на оси ординат, D=OD=(x,0)
–
ординаты.
;
– отсекаемого
касательной на оси ординат, D=OD=(x,0)
–
ординаты.
Замечание: Условие задачи предполагает равенство величин: |OТ| = x2
Для лучшего восприятия задачи воспользуемся рисунком: отрезки ОА и МD выделены красным цветом. Через некоторую точку М(x,y) плоскости OXY проходит кривая y=(y) со свойством:
▪ Случай-1: [отрезок OТ]= x2; (1)
▪ Случай-2: [отрезок OТ]= – x2. (2)
Случай-1.
0).
Из условия запишем: х–![]() =x2
–
дифференциальное уравнение для нахождения
кривой с заданными свойствами. Остается
решить это уравнение!
=x2
–
дифференциальное уравнение для нахождения
кривой с заданными свойствами. Остается
решить это уравнение!
1). Запишем уравнение в виде: (x–x2)dy–ydx=0 – уравнение с разделяющимися переменными.
2). Учитывая «Решение–В», запишем решения, которые следуют из исходной записи уравнения: x=0 – ось ОY; x=1 – прямая, параллельная оси ОY; y=0 – ось ОХ. Эти решения не отражают существа поставленной «геометрической задачи».
3).
Учитывая, что теперь x≠0,1
и y≠0,
запишем уравнение в виде:
=![]() ;
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
;
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
4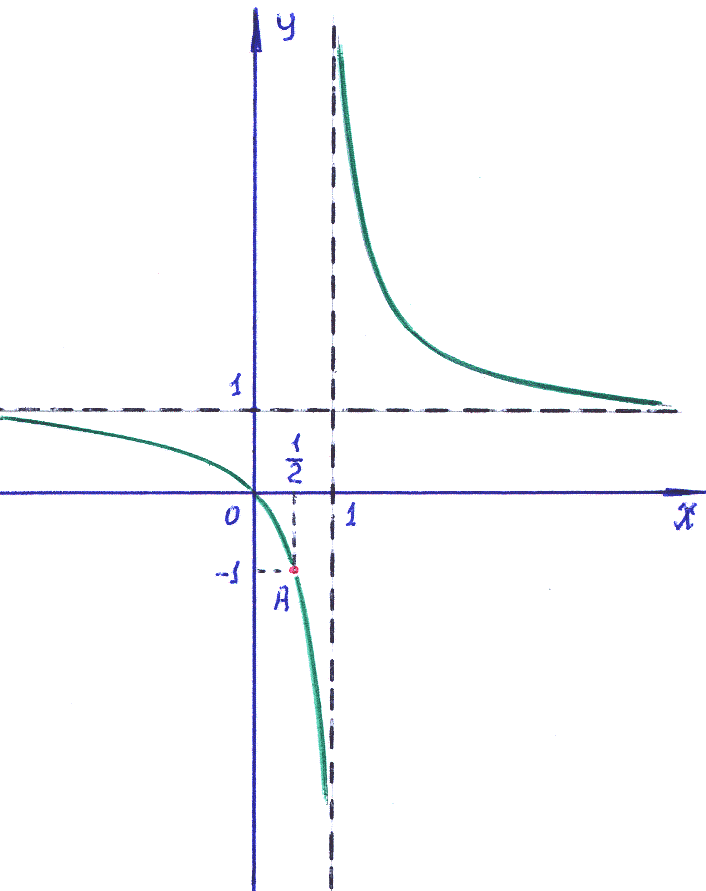 ).
Интегрируем:
+C=
).
Интегрируем:
+C=![]() или lnCy=ln
или lnCy=ln![]() ,
лучше: y=C
=С
,
лучше: y=C
=С![]() –
общее решение дифференциального
уравнения: семейство гипербол.
–
общее решение дифференциального
уравнения: семейство гипербол.
Замечание:
Если
на плоскости XOY
изобразить простейшую гиперболу y=
,
то гиперболу y=
![]() получают смещением оси OY
на 1 влево. Если гиперболу y=
принять за «базовую», то семейство
кривых y=С
получают применением преобразований:
получают смещением оси OY
на 1 влево. Если гиперболу y=
принять за «базовую», то семейство
кривых y=С
получают применением преобразований:
а) для С>0 : ▪ поднять «базовую» кривую на С единиц; ▪ деформировать (сжать-растянуть) «базовую» кривую в С раз;
б) для С<0 : ▪ зеркально отобразить «базовую» относительно оси ОХ; ▪ опустить «базовую» кривую на |С| единиц; ▪ деформировать (сжать-растянуть) «базовую» кривую в |С| раз;
5). Интегральная кривая, проходящая через точку А= : y=1+ – частное решение дифференциального уравнения при С=1 (см. рисунок).
Случай-2.
0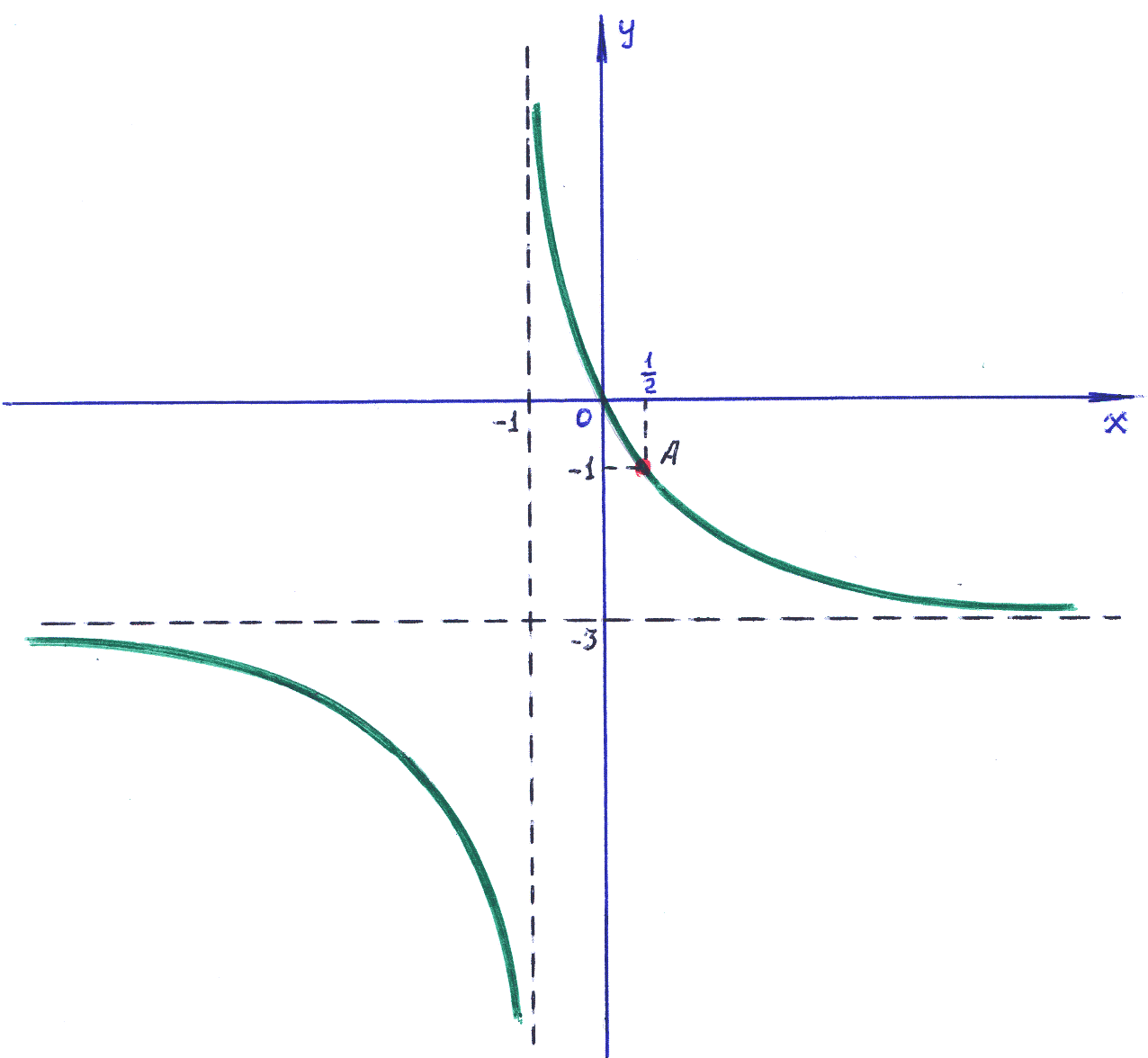 ).
Из условия запишем: х–
=–x2
–
дифференциальное уравнение для нахождения
кривой с заданными свойствами. Остается
решить это уравнение!
).
Из условия запишем: х–
=–x2
–
дифференциальное уравнение для нахождения
кривой с заданными свойствами. Остается
решить это уравнение!
1). Запишем уравнение в виде: (x+x2)dy–ydx=0 – уравнение с разделяющимися переменными.
2). Учитывая «Решение–В», запишем решения, которые следуют из исходной записи уравнения: x=0 – ось ОY; x=–1 – прямая, параллельная оси ОY; y=0 – ось ОХ. Эти решения не отражают существа поставленной «геометрической задачи».
3).
Учитывая, что теперь x≠0,–1
и y≠0,
запишем уравнение в виде:
=![]() ;
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
;
«видим!»: переменные разделились →
можно приступить к интегрированию ДУ!
4).
Интегрируем:
+C=![]() или lnCy=ln
или lnCy=ln![]() ,
лучше: y=C
=C
,
лучше: y=C
=C![]() –
общее решение дифференциального
уравнения: семейство гипербол.
–
общее решение дифференциального
уравнения: семейство гипербол.
Замечание:
Если
на плоскости XOY
изобразить простейшую гиперболу y=
,
то гиперболу y=
![]() получают смещением оси OY
на 1 вправо. Если гиперболу y=
принять за «базовую», то семейство
кривых y=С
получают применением преобразований:
получают смещением оси OY
на 1 вправо. Если гиперболу y=
принять за «базовую», то семейство
кривых y=С
получают применением преобразований:
а) для С>0 : ▪ поднять «базовую» кривую на С единиц; ▪ деформировать (сжать-растянуть) «базовую» кривую в С раз;
б) для С<0 : ▪ зеркально отобразить «базовую» относительно оси ОХ; ▪ опустить «базовую» кривую на |С| единиц; ▪ деформировать (сжать-растянуть) «базовую» кривую в |С| раз;
5).
Интегральная кривая, проходящая через
точку А=
:
y=
–3
=
–3+![]() –
частное решение дифференциального
уравнения при С=–3
(см. рисунок).
–
частное решение дифференциального
уравнения при С=–3
(см. рисунок).
Ответ: Случай-1: y=С – общее решение ДУ. Случай-2: y=С – общее решение ДУ. Решения ДУ: x=0 и y=0 теряют привычный геометрический смысл, и мы их в этой задаче не выделяем!
* * * * * * * * * *
Домашнее задание
Дома |
Л-3 |
гл.10: № 2, 5, 12, 18, 22, 24, 27, 28, 29, 32, 45, 166. |
12 |
Пример 1–2:
Показать, что при любом действительном
значении параметра С заданная функция
y=x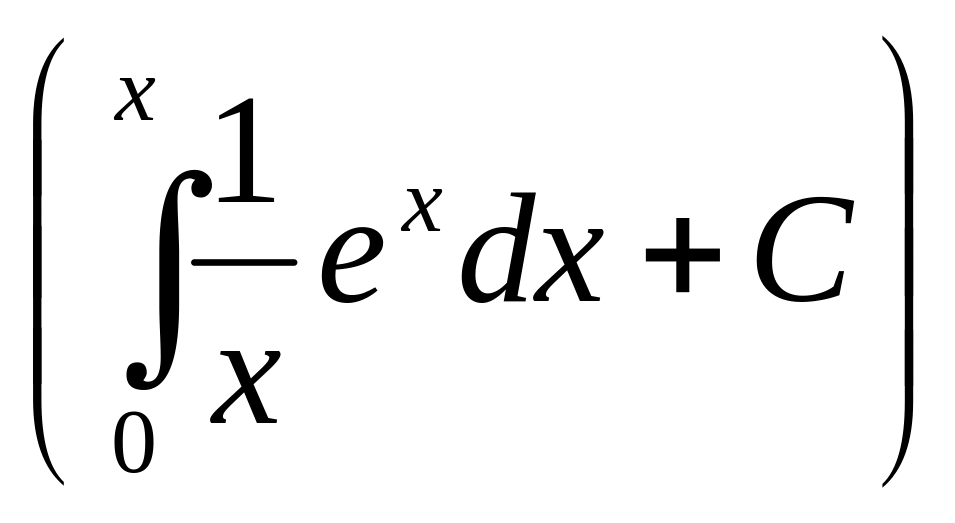 является решением ДУ: xy′–y
=xex.
является решением ДУ: xy′–y
=xex.
Решение:
1). Учтем, что производная функции равна: ex. Тогда производная заданной функции равна: y′= +x ex.= + ex
2). Подставим заданную функцию y и ее производную y′ в заданное ДУ:
x + xex – x = xex → тождество.
