26. Выведите дифференциальное уравнение затухающих гармонических колебаний и запишите его решение. Дайте определение логарифмического декремента затухания.

Пусть в системе действует сила вязкого трения, т. е. сила направленная против скорости движения груза, модуль которой прямо пропорционален скорости (см. рис. 1.2.1). (1.2.1.)

Запишем уравнение движения груза, составленное по 2-му закону Ньютона:

Подставим выражения для сил, тогда (6). Преобразуем выражение (6) к виду Введем обозначения   (частота собственных незатухающих колебаний или собственная частота) и   (коэффициент затухания), окончательно получим (7). Выражение (7) - это дифференциальное уравнение свободных гармонических затухающих колебаний. Решение уравнения (7) будем искать в виде: (8). Подставим (8) в (7) получим . Из полученного выражения найдем значения   : Если   (случай большого сопротивления), тогда имеем апериодическое решение в виде. Тогда решение будет в виде или т.е. получаем затухающее движение. Если   , тогда (9), где   - частота гармонических затухающих колебаний, т.е. получаем решение, соответствующее колебательному движению системы.

Логарифмический декремент затухания ϴ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. .

27. Какие колебания называют вынужденными? Запишите дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Выведите формулу для расчета резонансной частоты.

Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.

Линейное неоднородное дифференциальное уравнение: (147.5) Применяем впоследствии его решение для вынужденных колебаний конкретной физической природы (x₀ в случае механических колебаний равно F₀/m, в случае электромагнитных — U_m/L).

Решение уравнения равно сумме общего решения (146.5) однородного урав­нения и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме. Заменим правую часть уравнения (147.5) на комплексную величину х₀ :

(147.6). Частное решение этого уравнения будем искать в виде

Подставляя выражение для s и его производных   в уравнение (147.6), получаем

  (147.7). Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что h=w. Учитывая это, из уравнения (147.7) найдем величину s₀ и умножим ее числитель и знаменатель на 

. Это комплексное число удобно представить в экспоненциальной форме: , где (147.8); (147.9)

Следовательно, решение уравнения (147.6) в комплексной форме примет вид

Его вещественная часть, являющаяся решением уравнения (147.5), равна (147.10)

где А и j  задаются соответственно формулами (147.8) и (147.9).

Таким образом, частное решение неоднородного уравнения (147.5) имеет вид

(147.11). Решение уравнения (147.5) равно сумме общего решения однородного уравнения   (147.12). (см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являются гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от w.

РЕЗОНАНС - частотно-избирательный отклик колебат. системы на периодич. внеш. воздействие, при к-ром происходит резкое возрастание амплитуды стационарных колебаний. Наблюдается при приближении частоты внеш. воздействия к определённым, характерным для данной системы значениям. В линейных колебат. системах число таких резонансных частот соответствует числу степеней свободы и они совпадают с частотами собственных колебаний. В нелинейных колебат. системах, реактивные и диссипативные параметры к-рых зависят от величины стороннего воздействия, Р. может проявляться и как отклик на внеш. силовое воздействие, и как реакция на периодич. изменение параметров. В строгом значении термин "Р." относится лишь к случаю силового воздействия.

Из формулы следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту _рез, — частоту, при которой амплитуда А сме­щения (заряда) достигает максимума, — нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного выражения. 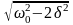Продифференцировав подкорен­ное выражение по  и приравняв его нулю, получим условие, определяющее _рез : Это равенство выполняется при =0, ± , у которых только лишь положи­тельное значение имеет физический смысл. Следовательно, резонансная частота

28. Какое явление называют резонансом? При каких колебаниях имеет место это явление? Получите формулу, связывающую резонансную частоту с собственной частотой и коэффициентом затухания колебательной системы. Начертите резонансные кривые для различных значений коэффициента затухания.

Определение и вывод в 27.