Теория кодирования

Словом в алфавите

A называется

любая

последовательность

букв этого алфавита: ai

ai

ai

...ai . Словом в алфавите B называется

1

2

3

s

любая

последовательность

букв

этого

алфавита bi

bi

bi ...bi

.

1

2

3

p

Множество слов алфавитов A и B обозначим ɱ ( A) и ɱ (B) .

Кодированием называется отображение

множества ɱ( A) на

множество

ɱ(B) . Кодом

слова

ai

ai

ai

...ai

называется

слово

1

2

3

s

ai

ai

ai

...ai

, принадлежащее ɱ(B) .

1

2

3

s

ai

Bi , i

1, 2,

...m,

Bi

ɱ(B) , Bi

Bj , если i j .

Тогда

кодом

слова

ai

ai ...ai

ɱ( A) будет последовательность

1

2

s

кодовых слов

ai

ai ...

ai

Bi

Bi ...Bi .

1

2

s

1

2

s

Набор кодовых слов K

B1, B2 ,...Bm

называется кодом.

ai

...ai

bj

...bj

можно однозначным образом разбить на кодовые

1

s

1

n

слова, то есть представить bj

...bj

в виде Bi

, Bi ...Bi .

1

n

1

2

s

Пример 1. Алфавит B

0,1 , алфавит A

a1, a2 , a3 ,

a1

0,

a2

01, a3

10, то есть K

0,01,10 .

Пусть a2a3a1

– слово в алфавите A,

a2a3a1

01100 . По этому

Рассмотрим в алфавите

B слово 010, его можно разбить на

кодовые слова двумя способами как B1B3 или B2 B1 , то есть коды двух

разных слов a1a3 и a2a1

совпали. Кодирование, заданное таким

Определение.

Префиксом

слова

c1 c2 ...ck

называется

любая

последовательность

c1 c2 ...cp ,

где

p

k .

Префикс

называется

собственным, если p

k .

Определение.

Суффиксом

слова

c1 c2 ...ck

называется

любая

последовательность

cq cq

1 ...ck , где

q

1,

суффикс

называется

собственным, если q

1.

Рассмотрим

M

{ }

– множество

собственных

префиксов и

и Bj

и непустые слова Br и Bs , принадлежащие ɱ B ,

такие что

Bi

Br и Bj

Bs .

Кодированию

сопоставим ориентированный граф G

V , E ,

где V

M

,

–пустое слово (слово без букв), M { 1,

2 ,... p } –

кодовых

слов.

Пара

i

j

E

тогда и

только

тогда,

когда

существуют

кодовые

слова

Bi

, Bi

,...Bi

s

0

, такие

что

1

2

s

i Bi Bi

...Bi

j

–

кодовое

слово.

При

этом

на

s

накладываются

1

2

s

следующие ограничения:

1)

если

i

и

j

, тогда s

0 ;

2)

если

i

или

j

, тогда

s

1;

3)

если

i

j

, тогда s

2.

Рис. 1

На рис.1 сверху показано одно разбиение слова

B на кодовые

слова, снизу другое.

Точки сечений не совпадают, так как B самое

короткое слово,

1,

2 , 3, 4 , 5 – собственные префиксы и суффиксы

кодовых слов. Тогда в графе G существует орцикл через вершину .

Действительно,

из

идет дуга в

1 , так как существует кодовое

слово Bj1

Bi1

1 , из 1

в

2

идет дуга, так как существует кодовое

слово Bi

1Bj

2 , из

2 идет дуга в

3 , так как существует кодовое

2

2

слово

Bj

2 Bi 3 ,

из

3

в

4 идет

дуга,

так

как

кодовое

слово

3

3

Bi

3

4

(в этом

случае

s

0 ),

из

4

в

5 идет дуга:

слово

4

Bj

4

5 ,

наконец,

из

5

в

идет дуга, так как существует слово

4

Bi

5 Bj Bj .

Найдя орцикл

1

2

3

4

5

, мы

5

5

6

2. Пусть кодирование взаимно однозначное, покажем, что в G

нет

орциклов

через

вершину

.

Доказательство

проведем

от

противного.

а) Рассмотрим самый короткий

цикл

через

вершину

–это

петля (рис. 2).

Но если из

в

идет дуга, то существуют

кодовые слова Bq , Bi

Bi

... Bi

s

2

такие,

что

1

2

3

Bq

Bi Bi ... Bi

, тогда

aq

ai

ai

... ai –

1

2

5

1

2

5

Рис. 2

декодирование неоднозначное.

б) Пусть орцикл проходит через две вершины (рис.3).

Рассмотрим

сообщение

вдоль

этого

цикла:

Bi

... Bi

Bj

... Bj

которое

допускает

два

1

s

1

q

разных разбиения на кодовые слова

Bi ... Bi

Bj

...Bj

Bi ...Bi

Bj

...Bj

,

где

Рис.3

1

s

1

q

1

s

1

q

Bj ...Bj и

Bi ... Bi

– разные кодовые слова

1

q

1

s

в) Рассмотрим произвольный орцикл через

вершину , тем не менее самый короткий, без

повторяющихся вершин (рис.4). Различные

разбиения на кодовые слова связаны с тем, куда

мы

будем

относить

вершины

i .

Одна

Рис.4

расшифровка будет такая:

Bi

... Bi

1Bj ...Bj

2 ... 3... Bj

...Bj

2 ...

3...

1

s

1

q

1

q

Другая расшифровка:

Bi ... Bi 1

Bj ...Bj

2 Bk ...Bk 3... Bj ...Bj

2 ...

3...

и

вновь

имеем

1

s

1

q

1

l

1

q

неоднозначное декодирование.

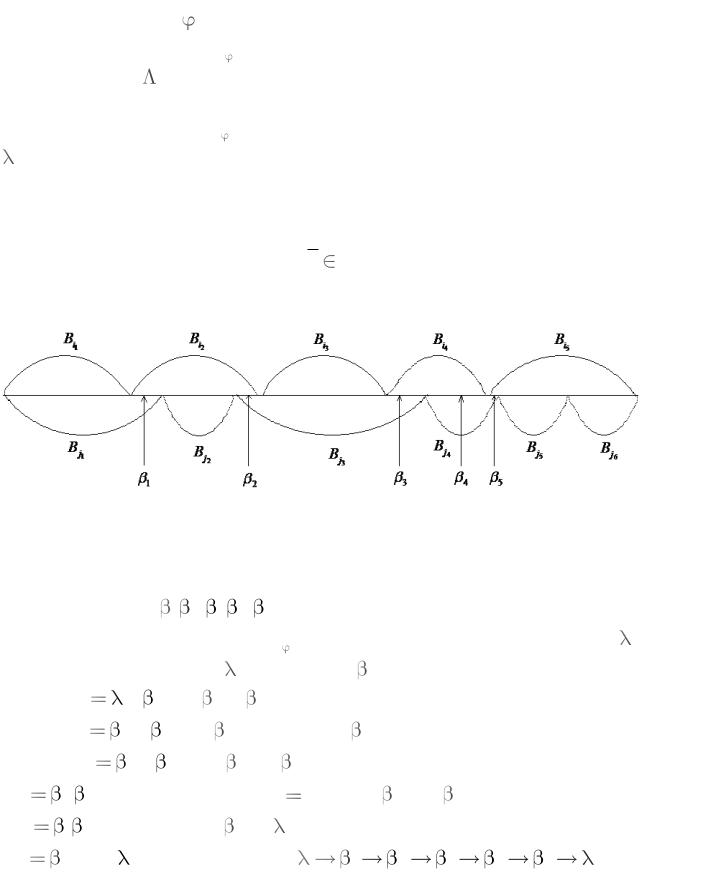
Пример 2. Рассмотрим код K

0, 01, 10

из примера 1, он был

вершину . Множество V

, 1 ,

из

идет

дуга в 1, так как

существуют кодовые слова 0 и 01 такие, что 01

B1 1, из 1 идет

дуга в , так как существует слово 10

1 B1 .

оканчивающегося на другое кодовое слово.

В нашем случае существует цикл (рис. 5) и

именно сообщение вдоль этого цикла допускает

различное

разбиение

на кодовые слова:

01 021 01

12 0102

10112 .

Рассмотрим

Рис. 5

простые типы взаимно однозначных кодов.

Рис.6

Рис.7

B1

01, B2 11, B3 000, B4

100, B5

0011, B6 1011,

B7

00100, B8 00101, B9

10100, B10

10101.

Теорема (неравенство Макмиллана).

Пусть заданы кодируемый алфавит A

a1,...am

и кодирующий

алфавит B

b1,...bk

. Взаимно однозначное кодирование

задано

набором кодовых слов K

B1, B2 ,...Bm с длинами

l1,l2 ,...lm

. Тогда

m

1

выполняется

неравенство

1,

где k

– количество

букв в

i 1 kli

алфавите B ,

m – мощность алфавита A.

m

1

Доказательство. Обозначим

x

и рассмотрим xn , где n

i 1

kli

– произвольное натуральное число.

xn

1

1

...

1 n

1

(1)

kl1

kl2

klm

(i1i2 ...in ) kli1

li2 ... lin

сумма берется по всевозможным упорядоченным наборам

i1i2 ...in ,

каждое 1

i

j

m ,

слагаемых будет mn . Для пояснения такой формы

записи приведем пример.

Пример 6. Рассмотрим x2 , где x

1

1

1

.

kl1

kl2

kl3

1

1

1

2

1

1

1

2

2

2

kl1

kl2

kl3

k

l1 2

k

l2

2

k

l3

2

kl1 kl2

kl1 k l3

k l2 k l3

1

1

1

1

1

1

1

1

1

kl1 l1

kl2

l2

kl3 l3

kl1 l2

kl2

l

kl1 l3

kl3 l1

kl2

l3

kl3 l2

Обозначим max l1,l2 ,...lm

lmax и, приведя подобные в равенстве

(1), получим

xn

nlmax

1

q

,

(2)

k r

r

r 1

где

r

li

li

...

li ,

qr

–

число

наборов

i1i2 ...in

на

которых

1

2

n

li

li ...

li

r . Если для какого-то r

не будет ни одного набора

1

2

n

i1...in , на котором li ...

li

r , соответствующее qr

0 .

1

n

Оценим

qr . Набору i1i2 ...in

соответствует единственное слово

ai

ai

...ai

ɱ

A . Так как упорядоченные наборы i1i2 ...in

различны, то

1

2

n

слова ai

ai

...ai

разные, кодирование

взаимно однозначные, их коды

1

2

n

Bi

Bi ...Bi

– слова в множестве ɱ

B

также различны. Длина слова

1

2

n

Bi

Bi ...Bi равна li

li

...

li

r .

1

2

n

1

2

n

Таким образом, qr

– число слов длины r в алфавите B , которые

алфавите B k r , поэтому q

k r ,

r

xn

nlmax

1

q

nlmax

1

k r

nl

k r

r

k r

max

r 1

r 1

Тогда x n nl

. Неравенство выполняется для любого n , можно

max

перейти к пределу при n

.

lim x

lim n nl

,

n

n

max

x от n не зависит, поэтому

lim x

x ,

lim n nl

1, следовательно,

n

n

max

m

1

x 1. Отсюда

1.

i 1 kli

Теорема о существовании префиксного кода

Пусть для алфавитов A

a1,

, am

и B b1,

,bk существует

взаимно-однозначный код

,

заданный набором кодовых слов

B1, B2 , , Bm

с длинами l1,l2 ,

,lm

, тогда для тех же алфавитов A

m

1

1.

(3)

i

1

kli

Пусть имеется cr кодовых слов длины r

и lmax max l1,l2 ,

,lm ,

тогда неравенство (3) можно переписать в виде (4)

lmax

c

r

1.

(4)

r

1

k r

Для любого l

lmax также будет справедливо

l

cr

1.

(5)

r

1

k r

Умножим обе части неравенства на k l

,

l

c kl

r

kl ,

(6)

r

r

1

Перепишем это неравенство в виде:

c kl 1

c kl z ...

c

k

c

kl ,

(7)

1

2

l

1

l

Откуда получим оценку для cl

– числа слов длины l в исходном

коде: c

kl

c kl 1

c kl 2 ...

c

k .

l

1

2

l

1

Докажем, что можно построить префиксный код, в котором

кодовых слов длины l также будет cl

l

1, 2,... lmax .

Доказательство проведем по индукции по l .