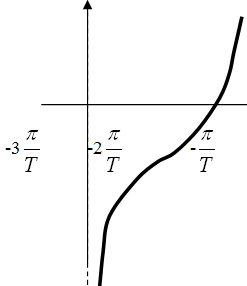- •1. Типовые воздействия и выходные характеристики систем.
- •2. Типовые динамические звенья и их характеристики.
- •2.1 Передаточная функция:
- •2.3. Лачх
- •2.4 Переходная характеристика
- •3. Классификация систем автоматического регулирования и систем автоматического управления.
- •4. Структурные схемы и передаточные функции (по лекциям Ахмадеева) Краткие сведения о структурных схемах
- •Правила структурных преобразований
- •Передаточные функции разомкнутых и замкнутых систем
- •Дополнительно
- •5. Блок-схема замкнутой системы автоматического регулирования, основные элементы и их назначение, принцип работы.
- •6. Качественные показатели сау.
- •7. Частотные методы исследования динамических систем и устройств.
- •8. Устойчивость, управляемость и наблюдаемость динамических систем и способы их оценки
- •Критерий устойчивости Михайлова
- •Критерий устойчивости Найквиста
- •1.Разомкнутая система устойчива
- •2.Разомкнутая система неустойчива
- •8. Устойчивость, управляемость и наблюдаемость динамических систем (новая редакция) Устойчивость линейных ситем. Необх и дост условие.
- •9. Непрямые методы оценки качества систем автоматического управления.
- •10. Запасы устойчивости по амплитуде и фазе.
- •Оценка устойчивости
- •11. Основные понятия и определения по нелинейным системам.
- •12.Дискретные системы и методы их исследования.
- •13. Математические модели. Классификация видов моделирования.
- •Классификация математических моделей
- •14. Основные этапы моделирования систем.
- •15. Основные способы формирования математических моделей динамических объектов
- •16. Дифференциальная форма математических моделей, передаточная функция. Передаточные функции разомкнутых и замкнутых систем
12.Дискретные системы и методы их исследования.
Основные понятия. Терминология. Квантование сигналов.
Дискретные САУ – это системы, в которых содержится одно или несколько звеньев, производящих квантование непрерывного сигнала в дискретный. Процесс преобразования непрерывной величины в дискретную называют квантованием. Различают квантование:
по
времени
значения непрерывного сигнала выделяются
в виде дискретных сигналов через равные
промежутки времени
![]() ,
при этом уровни сигнала могут принимать
произвольные значения
,
при этом уровни сигнала могут принимать
произвольные значения
![]()
по
уровню
осуществляется преобразование
непрерывного сигнала в дискретный в
произвольные моменты времени с выделением
значений непрерывного сигнала в момент
пересечения им равноотстоящих уровней
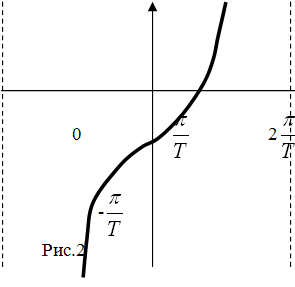
![]() (рис.2).
(рис.2).
![]()
смешанном квантовании происходит преобразование непрерывного сигнала в дискретный через равные временные промежутки, но при этом выделяется ближайший уровень непрерывного сигнала (рис.3).
![]()
В зависимости от вида квантования различают системы:
*Релейные – квантование по уровню.
*Импульсные – по времени
*Цифровые – по времени и по уровню.
Все релейные системы являются существенно нелинейными.
Импульсные системы (содержащие импульсный элемент) можно рассматривать как линейные.
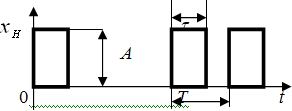
Импульсный
элемент
– устройство, осуществляющее квантование
сигнала по времени. Выходной сигнал
импульсного элемента представляет
собой последовательность импульсов.
При прямоугольной форме импульса его
можно охарактеризовать следующими
основными параметрами : высотой, или
амплитудой, импульса А;
длительностью, или шириной импульса
![]() ;
периодом повторения импульсов Т;
паузой между соседними импульсами Т-
;
скважностью
;
периодом повторения импульсов Т;
паузой между соседними импульсами Т-
;
скважностью
![]() .
.
Если имеем систему
![]() то
то![]()
Единичный прямоугольный импульс можно представить в виде разложения двух непрерывных функций
![]()
Введем
в рассмотрение идеальный импульсный
элемент, у которого функция формы
импульса есть дельта-функция
![]() .
.
Расчленим условно импульсный элемент на две части:
-простейший импульсный элемент; ()
-формирователь импульса (ФИ).
![]()
первый дает решетчатую функцию
![]()
Второй придает каждому импульсу определенную длительность и форму.
![]() .
.
Процесс преобразования квантовых сигналов в последовательность импульсов называется импульсной модуляцией.
В зависимости от типа модулятора системы делятся на линейные (АИМ) и нелинейные (ШИМ, ЧИМ)
Амплитудно-импульсная модуляция (АИМ) (амплитуда импульса пропорциональна входному сигналу);
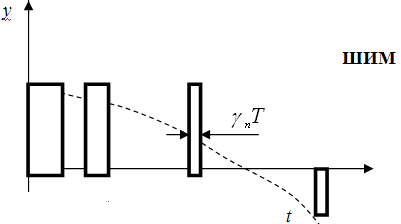
Широтно-импульсная модуляция (ШИМ) (ширина импульса пропорциональна входному сигналу);
Фазо-импульсная модуляция (ФИМ) (фаза импульса пропорциональна входному сигналу).

Длительность
![]() (0<<1)
Величина импульса x[nT]
(0<<1)
Величина импульса x[nT]
![]()
![]() .
.![]()
![]()
![]()
![]()

![]()
![]()
Рассмотрим амплитудно-импульсную модуляцию.
Период следования импульсов – период квантования.
![]() -
дискретное время, которое может быть
размерным и безразмерным
-
дискретное время, которое может быть
размерным и безразмерным
![]() -
целая часть от
-
целая часть от
![]() .
.
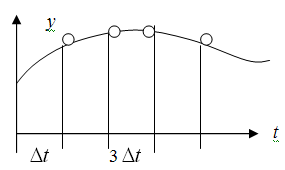
Функция
![]() - решетчатая функция (функция в конкретных
точках – узлах).)
- решетчатая функция (функция в конкретных
точках – узлах).)
(писать дальше по усмотрению)!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Z–преобразование. Модифицированное Z – преобразование. Обратное Z – преобразование
Метод Z – преобразования нашел широкое применение при исследовании импульсных и цифровых систем управления. Если поведение системы достаточно полно описывается только в дискретные моменты времени, то наиболее удобным математическим аппаратом для анализа и синтеза является аналог преобразования Лапласа – дискретное преобразование Лапласа или т.н. Z – преобразование.
Z
– преобразованием
решетчатой функции
![]() называется функция комплексного
аргумента Z,
определяемая выражением
называется функция комплексного
аргумента Z,
определяемая выражением
![]() ,(1)
,(1)
Это
выражение может быть получено следующим
образом. Если предыстория системы
относительно
![]() учитывается соответствующими граничными
условиями, то допустимо полагать, что
непрерывная функция времени
учитывается соответствующими граничными
условиями, то допустимо полагать, что
непрерывная функция времени
![]() при t<0.
В этом случае, как известно, функция
при t<0.
В этом случае, как известно, функция
![]() может быть заменена изображением по
Лапласу (одностороннее преобразование)
может быть заменена изображением по
Лапласу (одностороннее преобразование)
![]() (2)
(2)
Взяв
конечный интервал времени равным периоду
дискретности (![]() )
и представив текущее время в виде
последовательности
)
и представив текущее время в виде
последовательности
![]() можно в выражении (2) интеграл заменить
суммой, а величину dt
периодом квантования
:
можно в выражении (2) интеграл заменить
суммой, а величину dt
периодом квантования
:
![]() . (3)
. (3)
Выражение
(3) представляет собой дискретное
преобразование Лапласа. Предел этого
выражения при
![]() даст преобразование Лапласа непрерывной
величины (2).
даст преобразование Лапласа непрерывной
величины (2).
Если
обозначить
![]() ,
то
,
то
![]() (4)
(4)
(Обозначив![]()
При этом Z-преобразование, как следует из формулы (1), отличается от дискретного преобразования Лапласа только множителем Т, т.е.
![]() Итак,
преобразование Лапласа для дискретной
функции привело к бесконечной сумме.
Бесконечная сумма является функцией
комплексного переменного
.
Итак,
преобразование Лапласа для дискретной
функции привело к бесконечной сумме.
Бесконечная сумма является функцией
комплексного переменного
.
Операция
суммирования носит название прямого
дискретного преобразования Лапласа
(или Z-преобразования)
для решетчатой функции
в функцию комплексного переменного Z.
Эта операция кратко обозначается как
![]() И указывает, что
И указывает, что
![]() есть Z
– изображение решетчатой функции
или, короче,
есть Z
– изображение решетчатой функции
или, короче,
![]() .
Соответственно
является оригиналом
.
Изображение
существует, если (1) сходится.
.
Соответственно
является оригиналом
.
Изображение
существует, если (1) сходится.
Все
функции времени, имеющие одинаковые
значения в точках t=nT
оси времени, обладают одинаковыми
Z-преобразованиями
.
Это означает, что связь между функцией
времени
![]() и соответствующим ей Z-преобразованием
не является взаимно однозначной. Функция
характеризует только последовательность
чисел
,
но не позволяет судить о поведении
оригинала
внутри интервалов.
и соответствующим ей Z-преобразованием
не является взаимно однозначной. Функция
характеризует только последовательность
чисел
,
но не позволяет судить о поведении
оригинала
внутри интервалов.
Модифицированное Z-преобразование.
Если
значение Z-изображений
необходимо знать не только в дискретные
моменты времени t=nT,
но и в любые другие моменты времени,
смещенные на
по отношению к моментам квантования,
то можно использовать модифицированное
Z-преобразование:![]() (5)
(5)
где - действительный независимый параметр, принимающий произвольное значение от нуля до единицы. Модифицированное Z-изображение решетчатой функции либо определяется из формулы (5), либо следует использовать таблицы для модифицированного Z-преобразования.
Обратное
Z-преобразование
позволяет определить решетчатую
функцию-оригинал
или
![]() по ее Z-преобразованию
и сокращенно записывается в виде
по ее Z-преобразованию
и сокращенно записывается в виде
![]() или
или
![]()
При заданной существует три способа нахождения решетчатой функции: в виде бесконечного ряда, разложением на элементарные дроби и при помощи интеграла обратного преобразования.
Первый
метод
позволяет непосредственно получить
числовую последовательность
.
Если
представляет
собой рациональную функцию, т.е. отношение
двух многочленов, то разделив многочлен
числителя на многочлен знаменателя,
получим бесконечный ряд Лорана. Числовые
значения коэффициентов членов ряда
определяют дискреты решетчатой функции
![]() .
Указанный способ позволяет определять
сколь угодно большое число значений n.
При выполнении операции деления
многочлены числителя и знаменателя
следует записывать по возрастающим
степеням (
.
Указанный способ позволяет определять
сколь угодно большое число значений n.
При выполнении операции деления
многочлены числителя и знаменателя
следует записывать по возрастающим
степеням (![]() ).
).
Пример 1.
Дано:
![]()
Определить:
Решение:
![]()
Путем непосредственного деления получим
![]()
Отсюда
![]() ;
;
![]()
![]()
![]()
![]()
Второй
метод
основан на разложении функции
![]() на элементарные дроби и использовании
таблицы преобразования. Непосредственно
функция
на элементарные дроби и использовании
таблицы преобразования. Непосредственно
функция
![]() на элементарные дроби не раскладывается,
так как фигурирующие в таблице функции
от z
имеют в числителе множитель z.
на элементарные дроби не раскладывается,
так как фигурирующие в таблице функции
от z
имеют в числителе множитель z.
Пример 2.
Дано:
![]()
Определить:
.
Решение:
Разложим на элементарные дроби:
![]()
![]()
Из таблицы соответствия получим:
![]()
Третий метод нахождения решетчатой функции основан на интеграле обратного преобразования:
![]() или
или
![]()
В
этом случае интегрирование ведется по
окружности
![]() ,
где с
–
абсцисса абсолютной сходимости.
Окружность, по которой ведется
интегрирование, охватывает все особые
точки подынтегрального выражения.
Формулы обратного преобразования мало
применяются.
,
где с
–
абсцисса абсолютной сходимости.
Окружность, по которой ведется
интегрирование, охватывает все особые
точки подынтегрального выражения.
Формулы обратного преобразования мало
применяются.
Использование аппарата Z-преобразования позволило развить теорию линейных дискретных САУ, до некоторой степени аналогичную теории линейных систем непрерывного действия.
W – преобразование. Определение и свойства.
Для анализа и синтеза непрерывных САУ широко применяется частотный метод, основанный на построении логарифмических частотных характеристик. Простота и наглядность логарифмического частотного метода исследования непрерывных САУ вызывает естественное стремление использовать метод ЛЧХ для анализа и синтеза дискретных систем, возможное на основе w-преобразования.
Комплексная
переменная w
связана с комплексной переменной
![]() соотношением
соотношением
![]() (6)
(6)
Соотношение заданное в форме (6), получило название w-преобразование. Рассмотрим это преобразование подробнее, для чего запишем его в форме
![]() (7)
(7)
изменяя
переменную р
вдоль мнимой оси плоскости Р
т.е. полагая
![]() ,
найдем
,
найдем
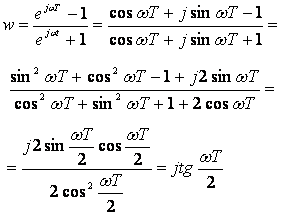
Правая
часть этого равенства – величина мнимая,
поэтому и левая часть будет мнимой
величиной. Вводя обозначение
![]() ,
получим
,
получим
![]() или
или
![]() (8)
(8)
Переменную
![]() называют псевдочастотой,
так как это безразмерная величина.
Реальная частота
называют псевдочастотой,
так как это безразмерная величина.
Реальная частота
![]() связана с псевдочастотой соотношением
связана с псевдочастотой соотношением
![]() (9)
(9)
Для исследования импульсных и цифровых систем в ряде случаев более удобна размерная псевдочастота , которая связана с псевдочастотой зависимостью
![]() (10)
(10)
Тогда![]() (11)
(11)
Переменную
называют абсолютной псевдочастотой.
Из выражения (10) следует, что при
![]() <<2
абсолютную псевдочастоту
в расчетах и при построении ЛЧХ можно
заменять действительной частотой
.
<<2
абсолютную псевдочастоту
в расчетах и при построении ЛЧХ можно
заменять действительной частотой
.
Соотношение (6) может быть представлено с учетом (11):
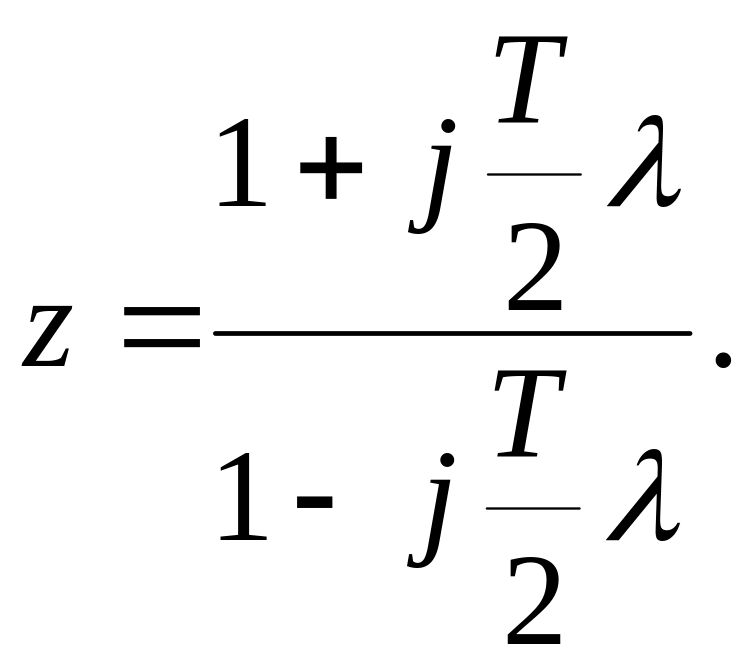 (12)
(12)
Поясним
смысл преобразования (6). Использование
подстановки
при замене р
на
![]() позволяет отобразить левую полуплоскость
плоскости Р
внутрь круга единичного радиуса плоскости
Z.
Функция
позволяет отобразить левую полуплоскость
плоскости Р
внутрь круга единичного радиуса плоскости
Z.
Функция
![]() является периодической функцией с
периодом
является периодической функцией с
периодом
![]() ,
поэтому для обхода всей окружности
единичного радиуса достаточно изменять
частоту в интервале
,
поэтому для обхода всей окружности
единичного радиуса достаточно изменять
частоту в интервале
![]() или в интервале
или в интервале
![]() .
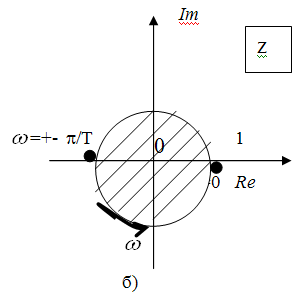
При этом отрезок мнимой оси от
.
При этом отрезок мнимой оси от
![]() до
до
![]() преобразуется в окружность единичного
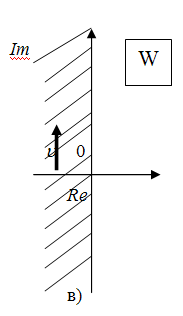
радиуса (рис.1, а, б). С помощью соотношения
(6) возможно отображение всех точек
Z-плоскости,
расположенных внутри круга единичного
радиуса, в соответствующие точки левой
полуплоскости W.
Подобные отображения получили название
конформных отображений (рис.1, б, в).
преобразуется в окружность единичного
радиуса (рис.1, а, б). С помощью соотношения
(6) возможно отображение всех точек
Z-плоскости,
расположенных внутри круга единичного
радиуса, в соответствующие точки левой
полуплоскости W.
Подобные отображения получили название
конформных отображений (рис.1, б, в).
При
изменении частоты
в интервале![]() абсолютная псевдочастота принимает
все значения, принадлежащие интервалу
абсолютная псевдочастота принимает
все значения, принадлежащие интервалу
![]() .
На рис.2 представлен график значений
псевдочастоты. Операция W-преобразования
в виде
.
На рис.2 представлен график значений
псевдочастоты. Операция W-преобразования
в виде
![]()
конформно
отображает левую полуполосу -
![]() ,
Re
q<0
плоскости q
(иначе р)
на левую полуплоскость плоскости W,
причем мнимая положительная полуось
плоскости W
является образом отрезка мнимой
положительной полуоси плоскости q
длиной
.
Начало этого отрезка находится в начале
координат.
,
Re
q<0
плоскости q
(иначе р)
на левую полуплоскость плоскости W,
причем мнимая положительная полуось
плоскости W
является образом отрезка мнимой
положительной полуоси плоскости q
длиной
.
Начало этого отрезка находится в начале
координат.
Понятие
псевдочастоты позволяет строить так
называемые логарифмические псевдочастотные
характеристики дискретных САУ.