Матрица 2х2

Обращение матрицы 2х2 возможно только при условии, что  .

С помощью матрицы алгебраических дополнений

C^T — транспонированная матрица алгебраических дополнений;

Полученная матрица A⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det. Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополненийэлементов исходной матрицы. Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем. Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

Тогда её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A ^{− 1} — матрицу, обратную к матрице A:  Так как A ^{− 1}A = E, получаем X = A ^{− 1}B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: .

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0.

Пример решения неоднородной слау

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.

Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.

Подставляя переменные в формулу, получаем:

Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.

Итак, x=2; y=1; z=4.

Вопрос 6.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).

Метод Крамера состоит в том, что 1. мы последовательно находим главный определитель системы , т.е. определитель матрицы А

 = det А

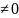
2. Вычисление n вспомогательных определителей  _i (i= ), которые получаются из определителя  заменой i-го столбца столбцом свободных членов.

3. вычисление значения неизвестных x _i =  _i / . Формула Крамера i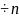

Если главный определитель системы  и все вспомогательные определители  _i = 0 (i=  ), то система имеет бесчисленное множество решений. Если главный определитель системы  = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.

Пример. Решить методом Крамера систему уравнений:

  x₁ +   x₂ +  x₃ +      x₄ = 5, x₁ + 2x₂ -   x₃ +    4x₄ = -2, 2x₁ -  3x₂ -   x₃ -     5x₄ = -2, 3x₁ +   x₂ +2x₃ + 11 x₄ = 0. Решение. Главный определитель этой системы

 

значит, система имеет единственное решение. Вычислим вспомогательные определители  _i ( i =  ), получающиеся из определителя  путем замены в нем столбца, состоящего из коэффициентов при x_i, столбцом из свободных членов:

              

                  

Отсюда x₁ =  ₁/ = 1, x₂ =  ₂/ = 2, x₃ =  ₃/ = 3, x₄ =  ₄/ = -1, решение системы - вектор С=(1, 2, 3, -1)^T.

Вопрос 7. Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Метод состоит из 2х частей: 1) Прямой ход. Путем элементарных преобразований строк расширенной матрицы привести основную матрицу к треугольному виду.

2) Обратный ход. Путем движения по преобразованной системе снизу вверх выразить значения переменных.

Пример. Решить систему уравнений методом Гаусса:  x +  y - 3z = 2, 3x - 2y +  z = - 1, 2x +  y - 2z = 0. Решение. Выпишем расширенную матрицу данной системы

и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

~  ;

б) третью строку умножим на (-5) и прибавим к ней вторую:

.

В результате всех этих преобразований данная система приводится к треугольному виду: x + y - 3z = 2, -5y + 10z = -7, - 10z = 13. Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим  x = - 0,7.