Вопрос 35 (36) Основные правила дифференцирования

Пусть  , тогда:

 

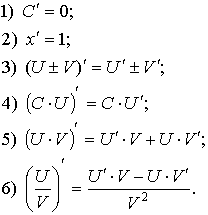
  7) Если  , то есть  , где   и  имеют производные, то   (правило дифференцирования сложной функции).

Основные правила дифференцирования. Произведение.

      Если функции u и v дифференцируемы в точке х₀, то их произведение дифференцируемо в этой точке и 

(uv)' = u'v+uv'.

      1) Найдем сначала приращение произведения: 

Δ(uv) = u(х₀+Δx)v(х₀+Δx)-u(х₀)v(х₀)=(u(х₀)+ Δu)(v(х₀)+ Δv)-u(х₀)v(х₀) =

=u(х₀)v(х₀)+ Δuv(х₀)+u(х₀) Δv+ΔuΔv-u(х₀)v(х₀)= Δuv(х₀)+u(х₀) Δv+ΔuΔv

      2)

      3) В силу дифференцируемости функций u и v в точке х₀ при Δx→0 имеем 

      Поэтому 

т. е. (uv)' = u'v+uv', что и требовалось доказать.        Следствие. Если функция u дифференцируема в х₀, а С — постоянная, то функция Сu дифференцируема в этой точке и 

(Сu)' = Сu'.

      Коротко говорят: постоянный множитель можно выносить за знак производной.        Для доказательства воспользуемся правилом 2 и известным из пункта о производной, фактом С' = 0: 

(Сu)' = Сu' + С'u = Cu' + 0⋅u = Cu'.

/mathanalis/limits/limits1.htm

Вопрос 36 (37) Экстремум функции

Функция y=f ( x ) называется возрастающей ( убывающей ) в некотором интервале, если при x ₁ < x ₂ выполняется неравенство f (x ₁ ) < f (x ₂ ) ( f (x ₁ ) > f (x ₂ )).

Если дифференцируемая функция y = f ( x ) на отрезке [ a , b ] возрастает (убывает), то ее производная на этом отрезке f ( x ) 0 ( f ( x ) 0).

Точка x _о называется точкой локального максимума ( минимума ) функции f ( x ), если существует окрестность точки x _о , для всех точек которой верно неравенство f ( x ) f ( x _о ) ( f( x ) f ( x _о )).

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума . Если точка x _о является точкой экстремума функции f ( x ), то либо f ( x _о ) = 0, либо f ( x _о ) не существует. Такие точки называюткритическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x _о - критическая точка. Если f ( x ) при переходе через точку x _о меняет знак плюс на минус, то в точке x _о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x _о экстремума нет.

Второе достаточное условие. Пусть функция f ( x ) имеет производную  f ( x ) в окрестности точки x _о и вторую производную    в самой точке x _о . Если f ( x _о ) = 0,   >0 (   <0), то точка x _о является точкой локального минимума (максимума) функции f ( x ). Если же   =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [ a,b ] функция y = f ( x ) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [ a,b ].

Либо Достаточные условия экстремума

Теперь определим достаточные условия для экстремума функции двух переменных. Так же как и для функции одной переменной, необходимый признак экстремума в случае многих переменных не является достаточным. Это значит, что из равенства нулю частных производных в данной точке вовсе не следует, что эта точка обязательно является точкой экстремума. Возьмем функцию Ее частные производные равны нулю в начале координат, однако функция экстремума не достигает. В самом деле, функция , будучи равной нулю в начале координат, имеет в любой близости к началу координат как положительные значения (в первом и третьем координатных углах), так и отрицательные (во втором и четвертом координатных углах), и значит, нуль не является ни наибольшим, ни наименьшим значением этой функции.

Достаточные условия экстремума для функции нескольких переменных носят значительно более сложный характер, чем для функции одной переменной. Мы рассмотрим эти условия без доказательства только для функции двух переменных.

Пусть точка является стационарной точкой функции

, т. е.

Вычислим в точке значение вторых частных производных функции и обозначим их для краткости буквами A, B и C:

Если , то функция имеет в точке экстремум: при A<0 и C<0 и минимум при A>0 и C>0 (Из условия следует, что A и C обязательно имеют одинаковые знаки).

Если, то точка не является точкой экстремума.

Если, то неясно, является ли точка точкой экстремума и требуется дополнительное исследование.

Пример:

1) Ранее в примере было установлено, что функция

имеет четыре стационарные точки:

Вторые частные производные данной функции равны

В точке имеем: A=10, B=0, C=2. Здесь ; значит, точка является точкой экстремума, и так как A и C положительны, то этот экстремум - минимум.

В точке соответственно будет A=-10, B=0, C=-4/3; .

Это точка максимума. Точки и не являются экстремумами функции (т.к. в них).

2) Найдем точки экстремума функции ;

Приравнивая частные производные нулю:

,

находим одну стационарную точку - начало координат. Здесь A=2, B=0, C= -2. Следовательно, и точка (0, 0) не является точкой экстремума. Уравнениеесть уравнение гиперболического параболоида (Приложение 2 (Рис. 2.)) по рисунку видно, что точка (0, 0) не является точкой экстремума.