20. Независимость случайных величин

Случайные величины ₁, ₂ называются независимыми, если для любых действительных чисел x₁,…,x_n R случайные события ( ₁<X₁),…, ( _n<X_n) независимы.

Из определения независимых событий вероятность появления должна равняться произведению вероятностей

P( ₁<X₁,…, _n<X_n )=P( ₁<X₁)…P( _n<X_n)

Случайные события независимы, если многомерная функция распределения равна произведению функций распределения координат.

1. Дискретные случайные величины

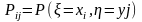
будут независимы, если

.

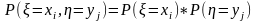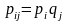для всех

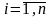
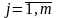
2. Непрерывные случайные величины

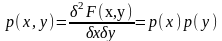
21. Условный закон распределения.

Условным законом распределения случайной величины , входящий в систему (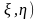 называется ее закон распределения, вычисленный при условии, что принимает значение у.

Пусть ( - непрерывный вектор с плотностью вероятности p(x,y). Пусть B=(y < 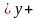∆y).Тогда условная функция распределения случайной величины при условии, что событие В произошло выглядит так

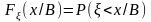
Пользуясь формулой умножения имеем

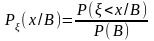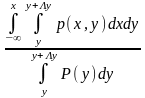= (1)

Функция 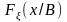называется условной функцией распределения случайной величины при условии В.

Возьмем производную от (1), устремив при этом ∆y к 0.

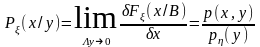по теореме о среднем для определённого интеграла.

Функция 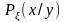называется условной плотностью вероятности случайной величины при условии, что равен у.

Из (2) следует аналогичная теорема умножения

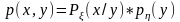(3)

Из (3) можем получить непрерывный аналог формулы полной вероятности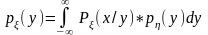

22. Неравенство Чебышева.

Последовательность случайных величин ₁, ₂ и т.д. сходится к по вероятности, если для >0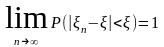

Неравенство Чебышева.Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине больше положительного числа 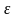, не больше чем, D(x)/ ² (дисперсия должна быть ограничена и )

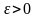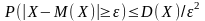
Докажем, это неравенство для непрерывной случайной величины с плотностью вероятности P(X)

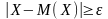
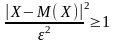
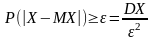
Неравенство Чебышева используется также для противоположного события:

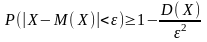
23.Теорема Чебышева. Теорема Бернулли.

Теорема Чебышева: Если X₁, X₂,…,X_n – последовательность независимых случайных величин, имеющих конечные дисперсии, ограниченные одним и тем же числом С, то для любого ε >0 выполняется

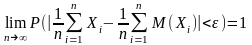
Доказательство. Введем в рассмотрение случайную величину – среднее арифметическое случайных величин

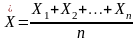. Найдем матожидание

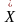
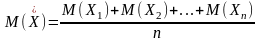
И дисперсию

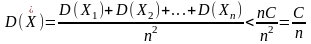
Следовательно – дисперсия конечная. Тогда к 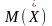применим неравенство Чебышева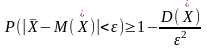

Переходя к пределу получим

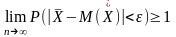
А так как вероятность не может быть больше 1, то предел равен 1.

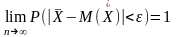
Суть закона больших чисел.

Если число случайных величин неограниченно растет, то их среднее арифметическое утрачивает смысл случайной величины и стремится к постоянному числу равному среднему арифметическому их матожиданий.

Следствием теоремы Чебышева является теорема Бернулли.

Пусть 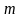- число появления события А в n испытаниях в схеме Бернулли, и p – вероятность появления А в одном испытании. Тогда для любого справедливо , 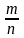-частота появления события.

Пусть 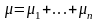, где - число появления события А в i-ом испытании.

Дисперсия любой величины 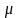равна произведению pq, так как p+q=1, то p*q не превышает ¼, и следовательно дисперсии всех величин ограничены числом c=1/4

Применим теорему Чебышева: 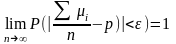так как матожидание равно вероятности наступления события.

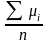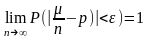Так как равна относительной частоте появления события А (m/n)(каждая величина _{1, 2}, _n при появлении события в соответствующем испытании равна 1 и поэтому их суму равна m), то окончательно получим , что и т.д.