5. Условная вероятность. Независимость событий.

Определение 1 Условной вероятностью события А при условии, что событие В уже произошло называется

P(A/B)=P(AB)/P(B), P(B)>0 (3.1)

Аналогично, условной вероятностью события B при условии, что событие A уже произошло называется

P(B/A)= P(AB)/P(A), P(A)>0 (3.2)

Из формул следует теорема умножения:

P(AB)=P(A)P(B/A)=P(B)P(A/B) (3.3)

Вероятность произведения двух произвольных событий равна произведению вероятности одного из событий на условную вероятность второго, при условии, что первое уже произошло.

Распространим теорему умножения на конечное число событий

P(A₁ A₂ A_k)=P(A₁)P(A₂/A₁)*…*P(A_k/A₁A_{2 …}A_k-1)

Определение 2 События А и В называются независимыми, если вероятность произведения равна произведению вероятности этих событий.

P(AB)=P(A)P(B) (3.4)

Сравнивая (3.3) и (3.4) получим, что для независимых событий условные и безусловные вероятности совпадают.

P(A/B)=P(A)

Для конечного числа независимых событий вероятность произведения равна произведению вероятностей.

P(A₁A₂…A_k)=P(A₁)P(A₂)…P(A_K)

6. Формула полной вероятности. Формула Байеса.

Пусть событие А может произойти только с одним из n несовместных событий H₁…H_n, образующих полную группу, т.е. Н_i * Н_j= Ø, i j, Н₁+… +Н_n=Ω.

События А*H_iи A*H_j являются несовместными.

Применяя теорему умножения к каждому слагаемому получим формулу полной вероятности.

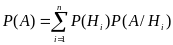
События H₁, H₂,…, H_n часто называют гипотезами.

Иногда интересует как перераспределяется вероятность гипотез, после того как событие А произошло P(H_i/A)

По теореме умножения вероятность произведения этих двух событий равна

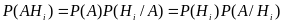
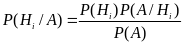
П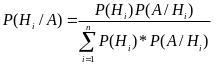 одставляя в знаменатель формулу полной вероятности получим формулу Байеса:

7. Схема независимых испытаний Бернулли.

Пусть производится n независимых испытаний в каждом из которых возможно только 2 исхода. Событие А или появится или не появится.

Обозначим вероятность появления события А – p, не появления – q.

Под элементарным событием в схеме Бернулли принимается последовательность наступления или ненаступления события А в n испытаниях

А={1}, 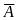={0}. Тогда элементарный исход имеет вид (1,0,…, 1)

Найдем вероятность того, что в n испытаниях событие появится ровно m раз.

Пример: Найдем сначала вероятность, что из 3 студентов 2 сдадут экзамен при том, что вероятность сдачи у каждого p.

Решение: n=3, m=2. При этом возможны следующие элементарные исходы

(1,1,0); (0,1,1); (1,0,1).

Вероятность каждого элементарного исхода одинакова и равна p²q.

Таким образом вероятность того, что из 3 испытаний событие p появится 2 раза

P₃(2)=3p²q.

Д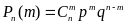 ля произвольных m и n вероятность одного элементарного исхода равна p^mq^n-m . Число таких элементарных исходов равно числу способов разместить m единиц по n местам, а это по определению число сочетаний m элементов по n. Получим формулу Бернулли (5.1)

Ч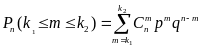 асто интересует появление события А не ровно m раз, а от k₁ до k_2.

При изменении n от 0 до m, вероятность в формуле Бернулли сначала растет, а затем убывает. Тогда можно указать такое число (m₀), при кот. вероятность будет наибольшей. При этом m₀ называется наивероятнейшим.

Можно показать, что m₀ вычисляется по формуле: m₀=np-q.

Если m₀ - не целое число, то его округляют до ближайшего целого с избытком, если m₀- целое, то наивероятнейших чисел два:

m`<sub>0</sub>=np-q и m`₀=np-q+1