36. Построение критической области.

Рассмотрим построение правосторонней критической области. Пусть вид распределения критерия k для проверки H₀ известен и его плотность P_k(X).

Критическую точку найдем из определения уровня значимости.

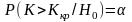
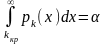; и p_k(x) известны.

Найдем K_кр

;

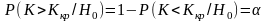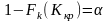
Рассмотрим построение двусторонней критической области

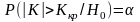
Раскроем знак модуля и перейдем к правосторонней критической области

;

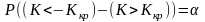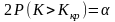
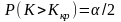
При компьютерном подходе на основании k наблюдаемого вычисляется минимальное значение уровня значимости при котором H₀ отвергается.

Если P мало(<0.05) то гипотезу отвергают.

37. Критерий согласия Пирсона.

Пусть вид распределения изучаемого признака Х неизвестен и пусть есть основание предполагать, что он распределен по некоторой функции F(x).

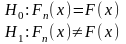
По выборке x₁,…x_n проверим H₀

Найдем максимальное и минимальные значения значение выборки, размах варьирования.

a=x_min, b=x_max

R=b-a

Разобьем R на k интервалов длины h=R/k.

Для начала для определения k можно использовать формулу Стерджеса. k=3.32 lg n

Пусть в результате получили интервалы z₀<z₁<…<z_k

Подсчитаем число вариант m_i попавших в каждый интервал.

Исходя из предположения о виде распределения F(x) вычислим теоретические частоты m_i и сравним их с эмпирическими.

Вычислим вероятность попадания случайной величины с функцией f(x) в построенные интервалы.

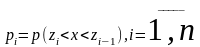
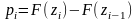
И на основании закона больших чисел

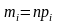
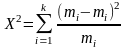
Можно показать, что при H₀ случайная величина 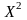имеет распределение (k-l-1) с числом степеней свободы (k-l-1).

Где k – число интервалов, l – число параметров предполагаемого распределения.

Проверка H₀ осуществляется следующим образом:

1. вычислить наблюдаемое значение критерия

по таблице критических точек распределения по выбранному уровню значимости

2. и числу степеней свободы (k-l-1).находят _кр

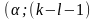
А). Если _набл< _кр, то говорят, что нет основания отвергнуть H₀, следовательно признак X имеет распределение F(x).

Б). Если _набл> _кр, то H₀ отвергаем и принимаем H₁.

Следовательно X имеет другое распределение.

38. Вычисление теоретических частот для нормального распределения.

Предположим, что признак Х имеет нормальное распределение. Пусть выборочные данные разбиты на интервалы и подсчитаны эмпирические частоты

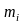
Для подсчета оценок параметров a и перейдем к дискретному ряду. 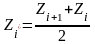,середины интервалов

1.

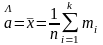
2.

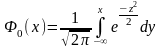
3.

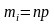
Замечания.

1)Чтобы эмпирически функция (m_i) распределения лучше описывала теоретическую нужно, чтобы число интервалов было больше.

2)Для выполнения предельной теоремы нужно, чтобы эмпирические частоты не должны быть маленькими.(>5)

Если какой то интервал содержит малые значения m_i, то соседние интервалы объединяются, а частоты складываются. Тогда число степеней свободы критерия Х² уменьшается на 1.

39. Cравнние дисперсий двух нормальных выборок.

Пусть имеется две выборки X и Y. Найти среднее их законов распределения.

Пусть есть основание предположить, что обе выборки имеют нормальное распределение.

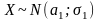
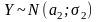
Эти нормальные распределения одинаковы в том случае, если равны их параметры а₁=а₂,

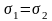
Проверим гипотезу о равенстве дисперсий:

H₀:

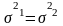
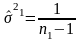
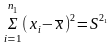
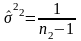
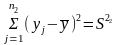
Для H₀

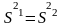
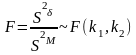где k1 и k2 – число степеней свободы

K1=n1-1 k2=n2-1

1)H₁:

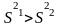
2)вычисляется

3)По таблице Фишера на основании α, k1, k2 и числа степеней свободы находят F_крит

Если F_H>F_крит то H₀ отвергают (дисперсии различаются достоверно) и наоборот

Пусть гипотеза H₁ двусторонняя. H₁: 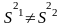Тогда проверка гипотезы осуществляется таким же образом, но при выбранном уровне значимости α F_крит(α/2,k₁,k₂)