32)Основное уравнение лпп системы

Очень часто линейную систему с постоянными параметрами реализуют в виде линейной цепи с сосредоточенными параметрами (емкости, индуктивности и т.д.).

В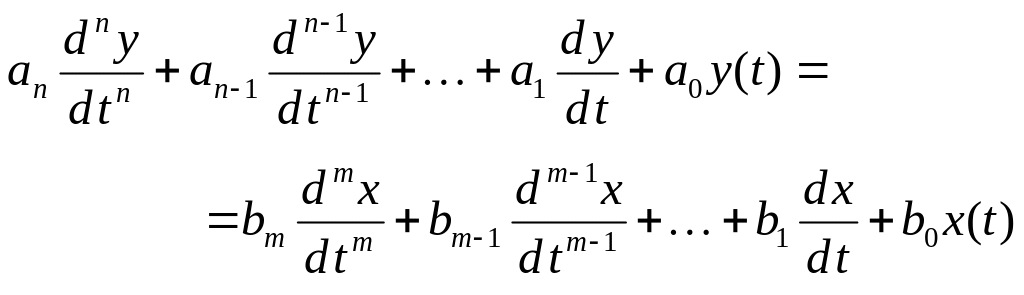 этом случае связь между входным x(t) и выходным y(t) сигналами может быть выражена в виде дифференциального уравнения.

(1)

В этом дифференциальном уравнении a_i,b_i, - постоянные коэффициенты. Кроме того, должно выполняться условие m £ n . Значение n называют порядком цепи.

Функция передачи системы

Д ифференциальное уравнение (1) обычно решают, используя преобразование Лапласа

Здесь s – комплексное число, а функция f(t) удовлетворяет условию f(t) = 0 для t < 0. Функцию f(t) называют оригиналом, а функцию F(s) –изображением Лапласа. Символически связь между изображением и оригиналом обозначим, так же как и для преобразования Фурье.

. Здесь H(s) называется функцией передачи и определяется формулой.

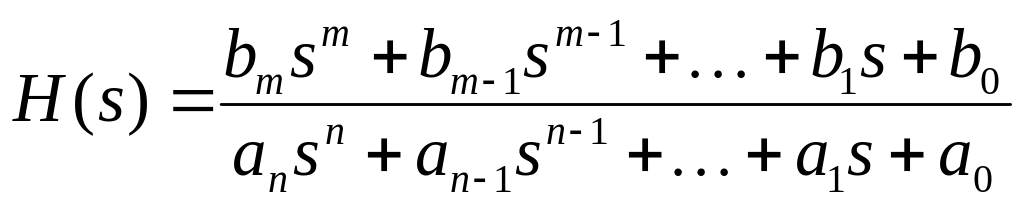
комплексный коэффициент передачи получается из

функции передачи путем замены аргумента.

Т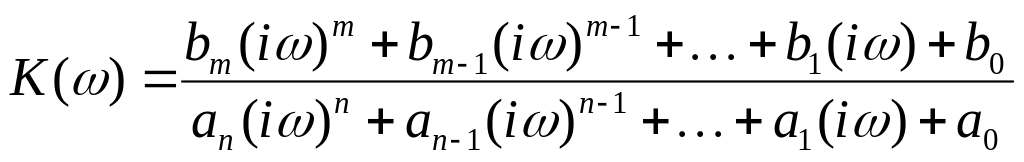 аким образом, для ЛПП системы комплексный коэффициент передачи вычисляется по формуле.

33)Нули и полюсы функция передачи системы

Разложив числитель и знаменатель функции передачи (27) на элементарные множители, мы получаем функцию передачи в следующем виде.

, Здесь k=b_n/a_n - коэффициент усиления. z_i – нули функции передачи,p_i - полюсы функции передачи. В точках нулей H(z_i)=0, а в точках полюсов H(p_i)=∞.

Для восстановления импульсной характеристики h(t) по заданной функции передачи H(s) надо использовать обратное преобразование Лапласа. Для нахождения обратного преобразования Лапласа обычно используется теория вычетов, связанная с полюсами функции передачи. Разбор способов нахождения вычетов, мы оставим до рассмотрения теории Z - преобразования.

34)Z – преобразование

Определение. Z – преобразованием числовой последовательности

я вляется функция комплексной переменно X(z). Эта функция определяется следующим образом.

(1)

Здесь радиус круга определяется как верхний предел

В дальнейшем, вместо подробного определения с помощью соотношений (1), будем изображать Z – преобразование следующей формулой (2)

При этом мы будем иметь в виду, что ряд (2) сходится снаружи круга |z| > r . Также снаружи этого круга Z-преобразование X(z) является аналитической функцией. Внутри же, этого круга |z| £ r Z-преобразование X(z) может иметь особые точки.

Напомним понятие аналитической функции комплексного переменного.

Функция комплексного переменного

является аналитической в точке z , если в этой точке существует производная.

Необходимым и достаточным условием аналитичности функции являются условия Коши – Римана.

В особых точках функция комплексного переменного, не является аналитической функцией.

Дальше Z – преобразование будем так же называть Z - образом числовой последовательности x(n) .Символически связь между последовательностью и ее Z - образом будем обозначать, так же как и для преобразования Фурье.