43)Рекурсивные и нерекурсивные фильтры и их связь с ких и бих фильтрами

Напомним, что основное разностное уравнение ЛДФ, имеет вид.

. Коэффициенты этого уравнения позволяют выразить переходную функцию фильтра с помощью формулы.

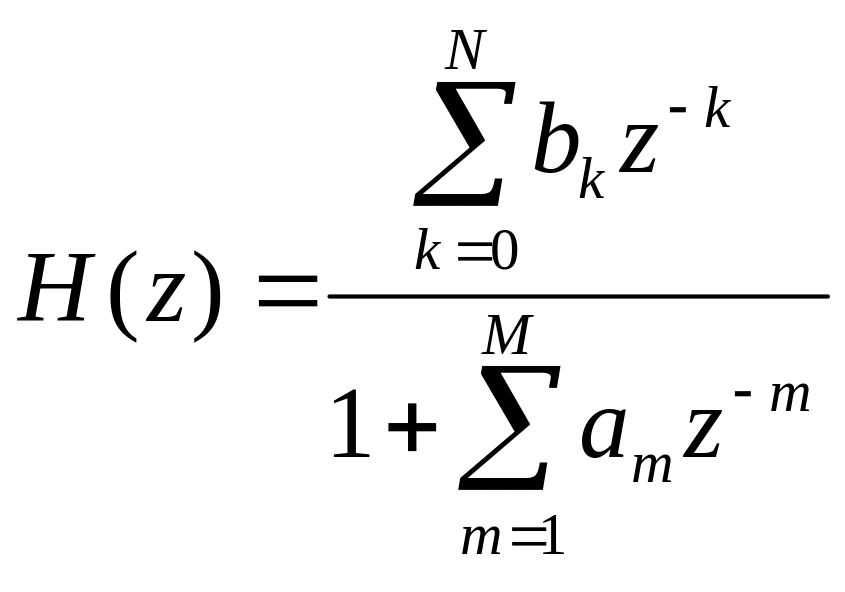
В зависимости от того, равны нулю все или не все коэффициенты a_n , фильтры разделяют на рекурсивные и нерекурсивные.

Если все коэффициенты a_n равны нулю, то мы получаем уравнение нерекурсивного фильтра . Нерекурсивный фильтр – это фильтр без обратных связей. Переходная функция нерекурсивного фильтра имеет вид . Найдем импульсную характеристику h(n) нерекурсивного фильтра. Вспомним, что импульсную характеристику называют так же реакцией системы на единичный импульс. Это означает, что если на вход ЛДФ подать единичный импульс в виде символа Кронекера, то на выходе получился сигнал, совпадающий с импульсной характеристикой h(n). В результате получим импульсную характеристику .

Таким образом, импульсная характеристика нерекурсивного фильтра находится очень просто, она равна коэффициентам b_k основного разностного уравнения фильтра.

Формула показывает, что полученная импульсная характеристика имеет конечное число отличных от нуля элементов, поэтому она является конечной импульсной характеристикой. Значит все нерекурсивные фильтры являются КИХ – фильтрами.

Исследуем нерекурсивные фильтры на устойчивость. Для этого переходную функцию нерекурсивного фильтра . Из переходной функции имеется одна особая точка z = 0. Эта особая точка для членов суммы является полюсом порядка m , где m - номер члена в сумме. Эта особая точка лежит в комплексной плоскости в центре единичного круга | z | < 1. Отсюда по теореме 2 следует, что фильтр устойчив. Значит все КИХ – фильтры являются устойчивыми фильтрами.

Рассмотрим фильтр с импульсной характеристикой . Формула показывает, что полученная импульсная характеристика имеет бесконечное число отличных от нуля элементов, поэтому она является бесконечной импульсной характеристикой. Таким образом, рассматриваемый рекурсивный фильтр является БИХ – фильтром. БИХ - фильтр неустойчив

Нерекурсивные->КИХ h(n)(КИХ – фильтры)->Устойчивы

Рекурсивные->КИХ (КИХ – фильтры)->Устойчивы

Рекурсивные->БИХ (БИХ – фильтры)->Устойчивы||Неустойчивы

44)Аналоговые фильтры

Как мы говорили ранее, в основе многих методов проектирования дискретных фильтров лежат методы проектирования аналоговых фильтров. Аналоговый фильтр относится к линейным системам с постоянными параметрами (ЛПП). Вспомним, что ЛПП (а значит и фильтр) описывается функцией времени h(t) - импульсной характеристикой. Эта функция определяется соотношениями.

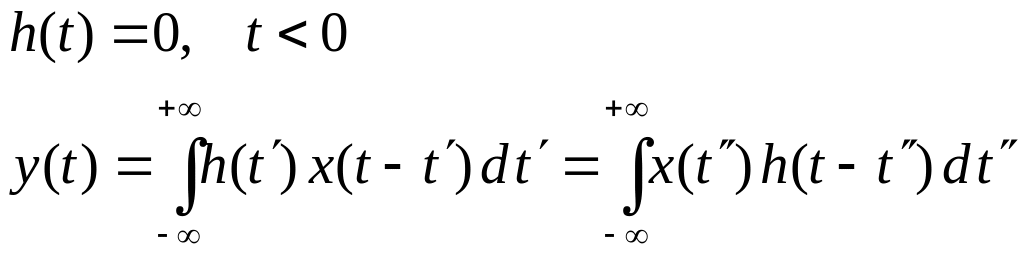x(t) входящий сигнал, а y(t) выходящий сигнал.

Комплексный коэффициент передачи фильтра является преобразованием Фурье импульсной характеристики .

Модуль и фазу комплексного коэффициента передачи называют амплитудно-частотной (АЧХ) и фазово-частотной (ФЧХ) характеристиками системы.

Классификация фильтров по их АЧХ

Ф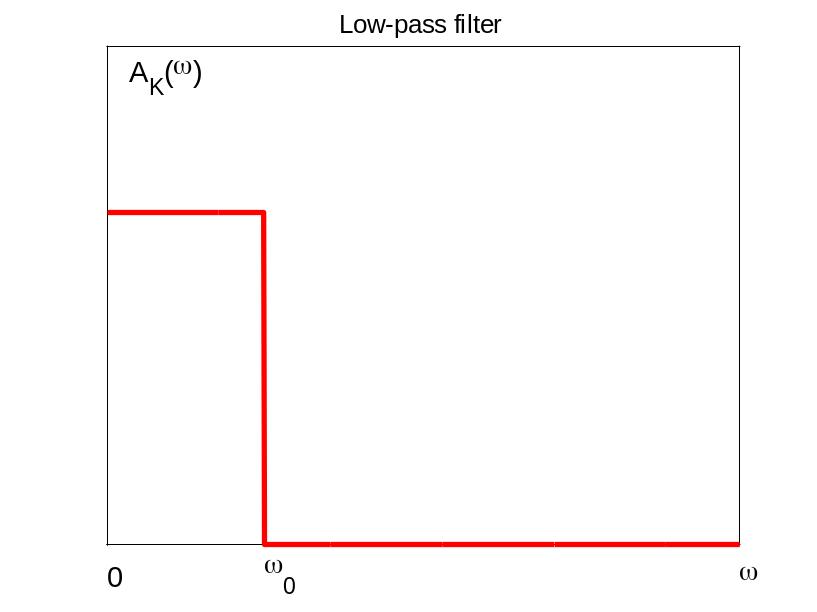 ильтры нижних частот (ФНЧ), пропускающие частоты, меньшие некоторой частоты среза w₀. На рисунке показана АЧХ идеального фильтра нижних частот

Ф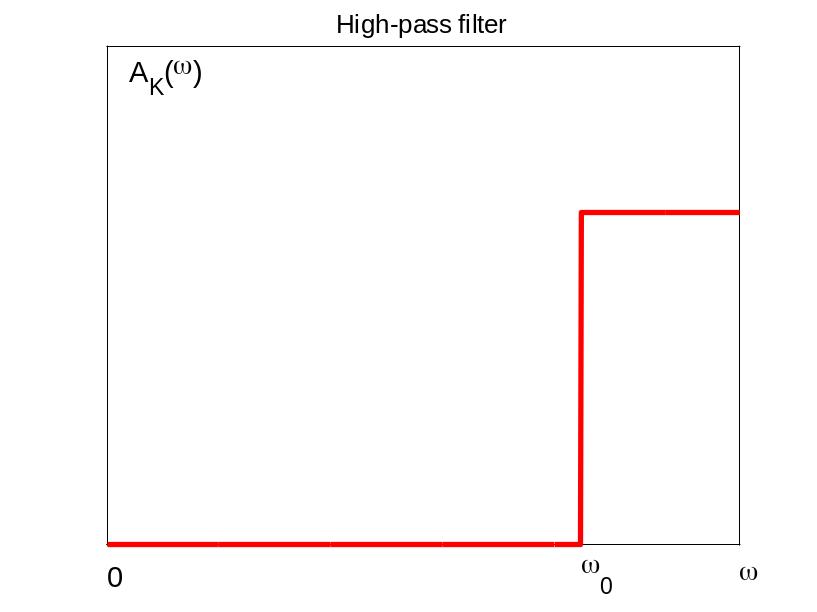 ильтры верхних частот (ФВЧ), пропускающие частоты, больше некоторой частоты среза w₀. На рисунке показана АЧХ идеального фильтра верхних частот.

П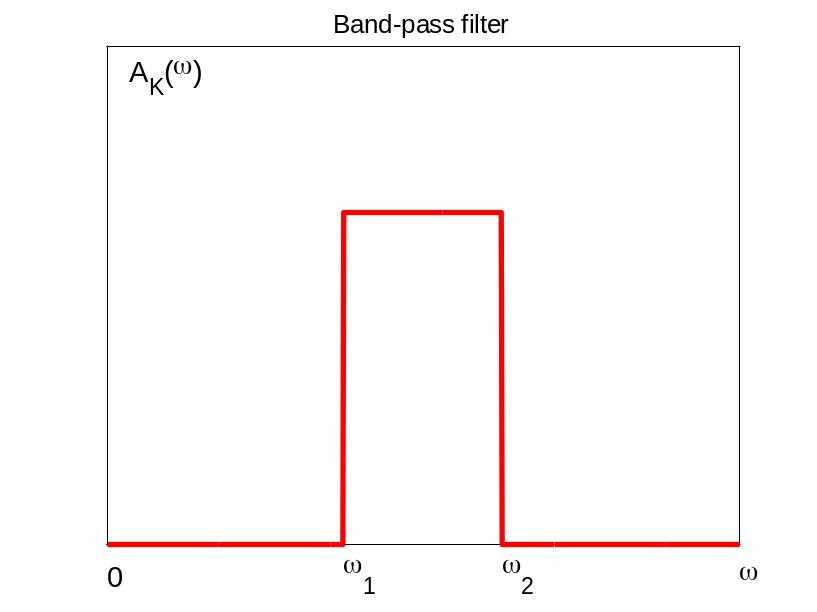 олосовые фильтры (ПФ), пропускающие частоты в некотором диапазоне [w₁;w₂). Такие фильтры характеризуются средней частотой и шириной полосы пропускания . На рисунке АЧХ идеального полосового фильтра.

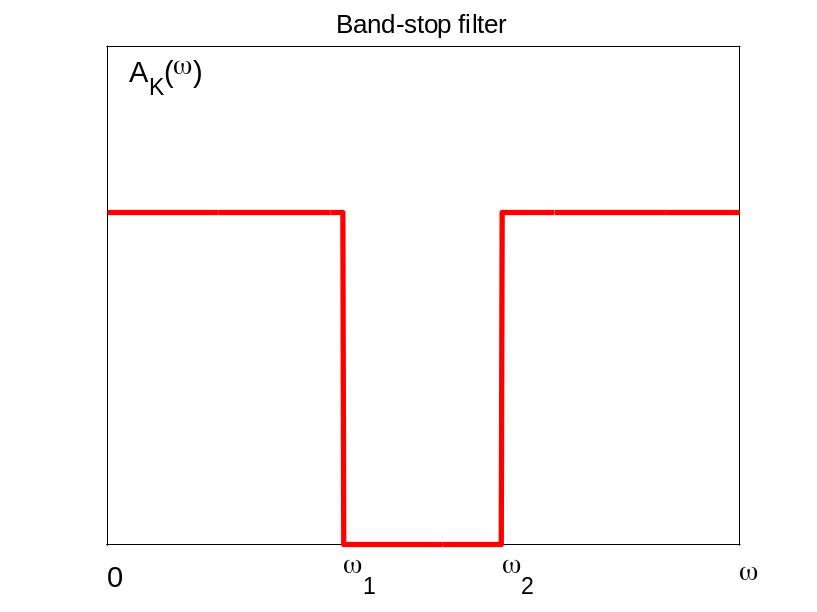
Режекторные фильтры (РФ). Режекторные фильтры – это фильтры пропускающие на выход все частоты, кроме лежащих в некотором диапазоне [w1, w2] . Такие фильтры характеризуются средней частотой w_c и шириной полосы задержки Dw .

45)Фильтры Баттерворта

Фильтры Баттерворта это фильтры нижних частот. Передаточная функция H(s) определяется n полюсами, которые задаются формулой.

. Здесь w₀ - некоторая заданная частота, называемая частотой среза. Полюсы лежат в комплексной плоскости на окружности радиуса w₀, потому что для них выполняется условие . Число n определяет порядок фильтра Баттерворта. Покажем расположение полюсов для фильтра Баттерворта 5-го порядка в комплексной s плоскости. Для простоты частота среза взята раной единице w₀=1 .

П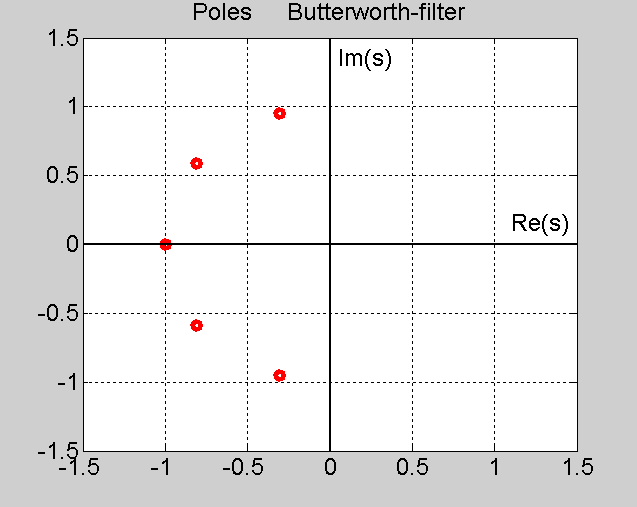 ередаточная функция H(s) для фильтра Баттерворта конструируется из полюсов следующим образом.

, k₀ нормировочный множитель.

комплексный коэффициент передачи:

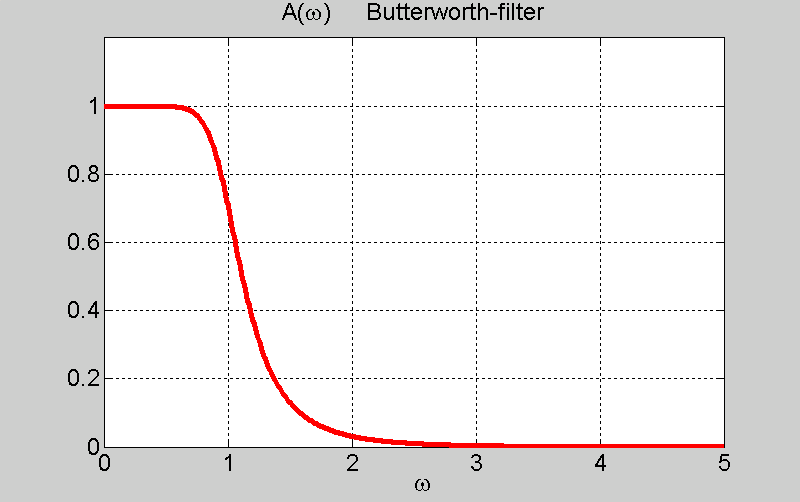
(1), откуда можно найти АЧХ и ФЧХ фильтра Баттерворта n - го порядка. Простые, но громоздкие вычисления позволяют получить для АЧХ простую аналитическую формулу. Если нормировочный множитель положить равным , то АЧХ фильтра Баттерворта будет выражаться формулой .

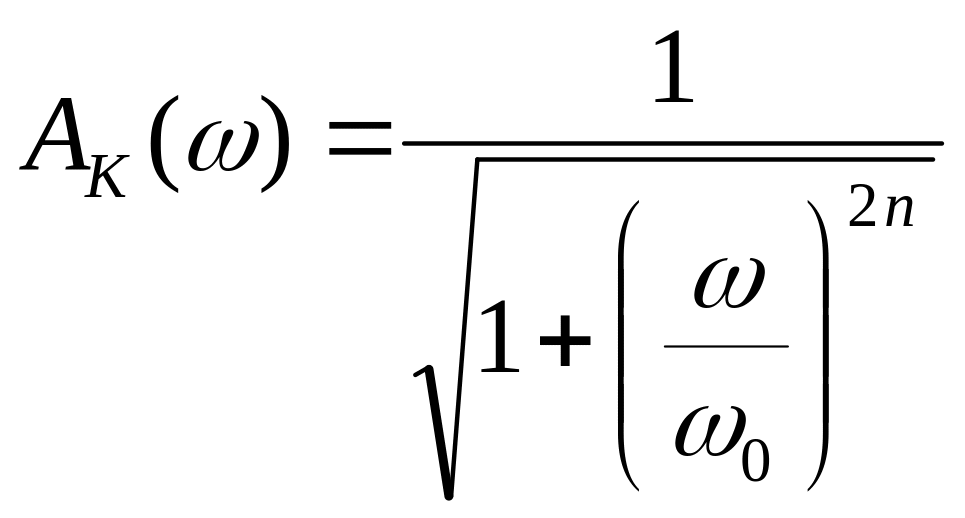АЧХ фильтра Баттерворта 5-го порядка. Частота среза взята раной единице w₀ = 1 .

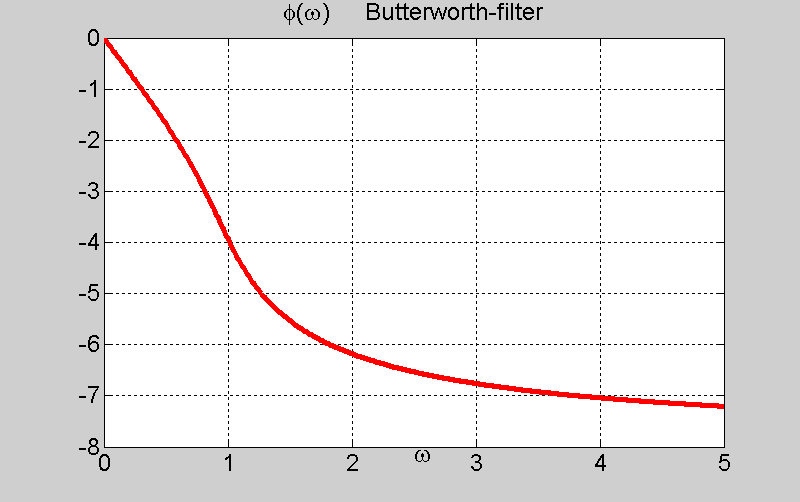
Для ФЧХ такой простой формулы как для АЧХ не существует. Поэтому надо брать формулу (1) и по ней находить ФЧХ.