37 Интегральный признак сходимости

рассм числовой ряд U1+U2+..+Un и пусть ф-ция f(x) такая, что f(1)=U1, f(2)=U2,f(n)=Un. Ряд (1) и интеграл(от1 до ∞) ∫ f(x)dx сходятся одновременно или расходятся одновременно.Доказательство. f(n)=Un построим ступенчатую ф-цию вписанную в кривую f(x) площадь фигуры U2+U3+…+Un+1<(ot1 do n+1) ∫f(x)dx перейдём к пределу пределу при n→ ∞, тогда пусть (от1 до ∞) ∫ f(x)dx - сходится = С тогда частичная сумма ряда ограниченна, а раз так то ряд сходится: пример. 1+1/2^2+1/3^2+1/n^2 (от1 до ∞) ∫dx/x^2=1

38 Знакопеременные ряды. Абсолютная и условная сходимость. Достаточное условие абсолютной сходимости знакопеременного ряда

24.2. Абсолютная и условная сходимость рядов.

Рассмотрим некоторый знакопеременный ряд (с членами произвольных знаков).

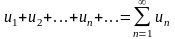(1)

и ряд, составленный из абсолютных величин членов ряда (1):

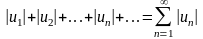(2)

Теорема. Из сходимости ряда (2) следует сходимость ряда (1).

Доказательство. Ряд (2) является рядом с неотрицательными членами. Если ряд (2) сходится, то по критерию Коши для любого >0 существует число N, такое, что при n>N и любом целом p>0 верно неравенство:

По свойству абсолютных величин: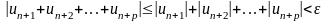

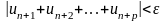
То есть по критерию Коши из сходимости ряда (2) следует сходимость ряда (1).

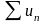Определение. Ряд называется абсолютно сходящимся, если сходится ряд .

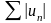Очевидно, что для знакопостоянных рядов понятия сходимости и абсолютной сходимости совпадают.

Определение. Ряд называется условно сходящимся, если он сходится, а ряд расходится.

Признак абсолютной сходимости является достаточным, но не необходимым. Например, ряд сходится по признаку Лейбница но ряд из абсолютных величин его членов расходится.

О: Знакопеременный ч.р. называется абсолютно сходящимся, если сходится ряд и условно сходящимся, если он сходится, хотя ряд расходится.

Например,   — абсолютно сходящийся ряд,  — условно сходящийся ряд.

39 Знакочередующиеся ряды. Теорема Лейбница

U1-U2+….+(-1)^n+1 * Un Ui>0 i=123n Если члены ряда убывают по абсолютной величине U1>U2>…>Un> И общий член ряда стремиться к нулю (n→∞)LimUn=0, то ряд сходится ДОК-ВО Запишем частичную сумму частного числа членов в таком виде: S2n>0 S2n=(U1-U2)+(U3-U4)+..+(U2n-1 – U2n) каждая скобка положительная по условию. И с увеличением n сумма возрастает. S2n= U1-(U2 – U3)+…+(U2n-2 - U2n-1) – U2n < U1 S2n<u1 С другой стороны частичная сумма четногочисла членов ограниченна . S2n S2n=S рассм сумму нечет числа членов S2n+1= S2n+U2n + 1 перейдем к пределу. (n→∞)Lim S2n+1= (n→∞)LimS2n+ (n→∞)LimГ2n+1+S+0=S=>этот ряд сходится Следствие При замене знакочередующегося ряда его отрезком пгорешность замены по абсолютной величине меньше первого отброшенного члена по абсолютной величине. S=Sn+rN S-Sn=rn S-Sn=Un+1(-1)^n+2+ +  gecnmUn+1-(Un+2-Un+3+….) |S-Sn|=|rn| < Un+1</u1

40 Свойства абсолютно и условно сходящихся рядов

 свойства абсолютно и условно сходящихся рядов.

Теорема.

Если ряд сходится абсолютно, то он является абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов. Это свойство не сохраняется для условно сходящихся рядов.

Теорема.

Если ряд сходится условно, то какое бы мы ни задали число А, можно переставить его члены, чтобы сумма ряда оказалась равной числу А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный в результате перестановки, окажется расходящимся.