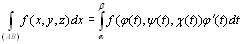- •1 Фигура, диаметр, мера. Определённый интеграл по фигуре (определение)
- •2 Масса фигуры переменной плотности
- •3 Геометрический смысл ди (двойного интеграла)
- •4 Геометрический смысл Кр и -1
- •5 Свойства определённого интеграла по фигуре
- •6 Вычисление криволинейного интеграла 1-ого рода
- •7 Вычисление ди в декартовых координатах
- •8 Вычисление ди в полярных координатах
- •9 Вычисление тройного интеграла в декартовых координатах
- •10 Вычисление Тройного интеграла в цилиндрических координатах
- •11 Вычисление тройного интеграла в сферических координатах
- •12 Вычисление пи-1
- •13 Вычисление статических моментов фигуры
- •14 Вычисление координат центра тяжести фигуры
- •15 Вычисление моментов инерции фигуры
- •Связь между криволинейными интегралами 1 и 2 рода.
- •17 Формула Грина
- •18 Независимость Кр и-2 от пути интегрирования
- •20. Формула Стокса
- •21 Формула Остроградского-Гаусса
- •22. Скалярное поле. Линии и поверхности уровня скалярного поля. Производная по направлению.
- •23 Градиент, свойства градиента
- •24 Векторное поле, определение, векторные линии, труба
- •25 Поток векторного поля, его физический смысл
- •26 Дивергенция векторного поля, её свойства
- •27 Циркуляция векторного поля, её физический смысл
- •28 Ротор векторного поля, его свойства
- •29 Оператор Гамильтона, диф.Операции 1-го и 2-го порядка
- •30 Простейшие векторные поля: потенциальное, соленаидальное, гармоническое
- •31 Определение числового ряда, основные понятия. Необходимые и достаточные условия сходимости ряда
- •32 Свойства сходящихся числовых рядов
- •33 Необходимое условие сходимости ряда. Достаточное условие расходимости числового ряда
- •34 Признаки сравнения числовых рядов
- •35 Признак д'Аламбера
- •36 Радикальный признак Коши
- •37 Интегральный признак сходимости
- •38 Знакопеременные ряды. Абсолютная и условная сходимость. Достаточное условие абсолютной сходимости знакопеременного ряда
- •24.2. Абсолютная и условная сходимость рядов.
- •39 Знакочередующиеся ряды. Теорема Лейбница
- •40 Свойства абсолютно и условно сходящихся рядов
- •41 Функциональные ряды, основные понятия
- •42 Равномерная сходимость функциональных рядов. Критерий равномерной сходимости. Теорема Вейештрасса
- •25.3. Свойства равномерно сходящихся рядов.
- •44 Степенные ряды. Теорема Абеля
- •45 Свойства степенных рядов
- •46 Ряд Тейлора. Теорема о единственности разложения функции в ряд Тейлора
- •47 Необходимое и достаточное условие разложимости функции в ряд Тейлора
- •48 Разложение в ряд Маклорена простейших функций
- •49 Приложения степенных рядов к приближенным вычислениям: а) вычисление значений функции; б) вычисление ои; в) решение диф. Уравнений
- •1Функции
- •50 Ряды Фурье. Разложение в ряд Фурье функций заданных на [- ], [0,2 ], [-l,l], а также чётных и нечётных функций, функций заданных на [0, ]
- •51 Ортогональные системы функций. Скалярное произведение функций
10 Вычисление Тройного интеграла в цилиндрических координатах
Рассмотрим цилиндрическую систему координат: Оrφz, которая совмещена с декартовой системой координат Оxyz(рис. 2.19).
При
этом
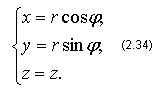
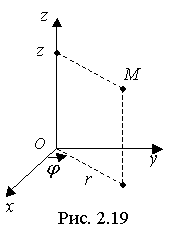
Вычислим Якобиан перехода от декартовой системы к цилиндрической:
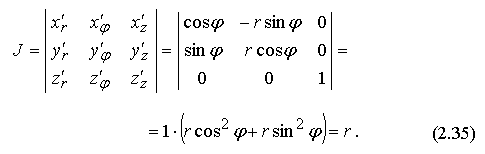
Следовательно, 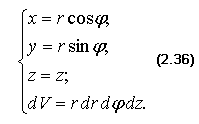
Тогда тройной интеграл примет вид:
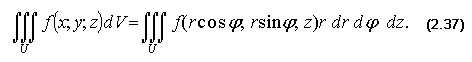
11 Вычисление тройного интеграла в сферических координатах
Рассмотрим сферическую систему координатОρΘφ, совмещённую с декартовой системой Оxyz. При этом максимальные пределы изменения сферических координат таковы: 0 ≤ φ ≤ 2π, 0 ≤ ρ ≤ ∞
Из рис. 2.21 нетрудно вывести следующие формулы, связывающие декартовые и сферические координаты:

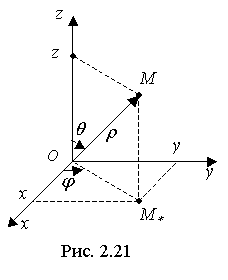
с помощью которых получим Якобиан преобразования:
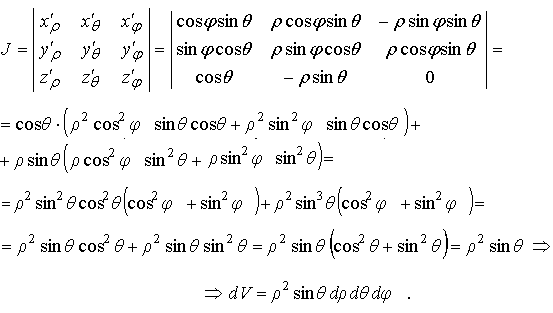
Таким образом, переход к сферическим координатам в тройном интеграле осуществляется по формулам:
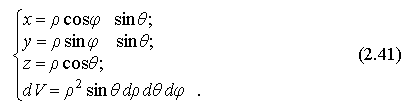
12 Вычисление пи-1
Поверхностный
интеграл первого рода от
функции ![]() по
поверхности S определяется
следующим образом:
по
поверхности S определяется
следующим образом:
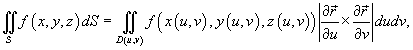
где
частные производные ![]() и
и ![]() равны
равны

а  означает
векторное произведение. Вектор
перпендикулярен
поверхности в точке
означает
векторное произведение. Вектор
перпендикулярен
поверхности в точке 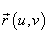 .
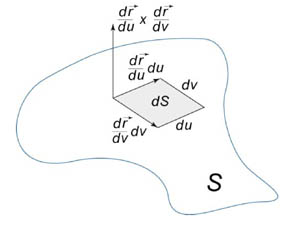
Абсолютное
значение
.
Абсолютное
значение 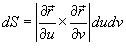 называется элементом
площади:
оно соответствует изменению площади dS в
результате приращения координат u и v на
малые значения du и dv (рисунок
1).
называется элементом
площади:
оно соответствует изменению площади dS в
результате приращения координат u и v на
малые значения du и dv (рисунок
1).
|
13 Вычисление статических моментов фигуры
статические
моменты фигуры на плоскости. Пусть
в декартовой системе координат на
плоскости задана фигура, ограниченная
кривыми ![]() , x = a, x = b
, x = a, x = b ![]() и
для x [a; b]
и
для x [a; b] ![]() .
.
Если плотность постоянна ( = 1), то статические моменты фигуры относительно осей координат выражаются формулами:
![]() ;
;
![]() .
.
Пример
3. Вычислить
статический момент фигуры, ограниченной
линиями ![]() относительно
оси ОХ.
относительно
оси ОХ.
Решение. Кривые ![]() пересекаются
в точках (0;0) и (1;1). На отрезке x [0,1]
выполняется неравенство
пересекаются
в точках (0;0) и (1;1). На отрезке x [0,1]
выполняется неравенство ![]() ,
поэтому
,
поэтому
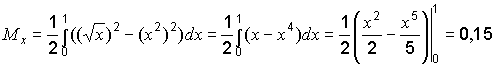 .
.
14 Вычисление координат центра тяжести фигуры
ентр тяжести фигуры, заданной на плоскости, имеет координаты
![]() ,
,
где ![]() –
статические моменты фигуры относительно
осей координат; S –
площадь фигуры.
–
статические моменты фигуры относительно
осей координат; S –
площадь фигуры.
Пример
5. Определить
координаты центра тяжести области,
ограниченной первой аркой циклоиды x = a(t
– sint), y = a(1
– cost), ![]() , a > 0
и осью ОХ.
, a > 0
и осью ОХ.
Решение. Вычислим площадь фигуры и статические моменты:
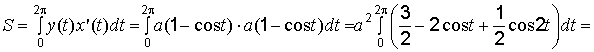
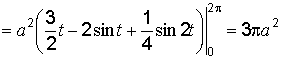 ;
;
![]()
 ;
;
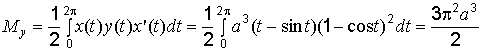 .
.
Подставив полученные результаты в формулы, найдем координаты центра тяжести:
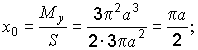
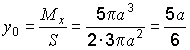 .
.
15 Вычисление моментов инерции фигуры
Момент инерции фигуры можно вычислять относительно плоскостей, осей координат и начала координат:
 ,
,
здесь ![]() есть
квадрат расстояния точки
есть
квадрат расстояния точки ![]() ,
,
до
соответствующего
объекта. Например, если
,
,
до
соответствующего
объекта. Например, если ![]() или
или ![]() ,
–
плотность распределения массы по
фигуре
,
то
,
–
плотность распределения массы по
фигуре
,
то
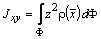 ,
, 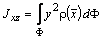 ,
, 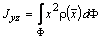 –
–
моменты инерции материальной фигуры относительно соответствующей координатной плоскости;
![]() ,
, ![]() ,
, ![]() –
–
моменты инерции материальной фигуры относительно соответствующей оси координат;
![]() – момент
инерции материальной
фигуры
относительно начала координат.
– момент
инерции материальной
фигуры
относительно начала координат.
16 Кр И-2, определение, вычисление, свойства, связь с Кр И-1, физический смысл
Если
существует конечный предел при ![]() интегральной
суммы
интегральной
суммы ![]() ,
не зависящий от способа разбиения кривой
на отрезки и выбора точек Mi, то от
называется криволинейным интегралом
второго рода от функции f(M) по кривой L
и обозначается
,
не зависящий от способа разбиения кривой
на отрезки и выбора точек Mi, то от
называется криволинейным интегралом
второго рода от функции f(M) по кривой L
и обозначается
![]() .
.
Свойства криволинейного интеграла 2-го рода.
Если функции P(M), Q(M), R(M) непрерывны на кривой (АВ), то интеграл (10.6) существует (справедливость этого утверждения следует из определения 10.2).
2 При изменении направления кривой (то есть перемены местами начальной и конечной ее точек) криволинейный интеграл 2-го рода меняет знак:
![]()
Вычисление