1 Фигура, диаметр, мера. Определённый интеграл по фигуре (определение)
Под фигурой Ω будем понимать ограниченное замкнутое тело с вкл. гран. Множ. Диаметр d фигурыΩ будем называть максимальное из расстояний между двумя точками этой фигуры . Для эллипса – большая ось. Под мерой ω для плоской фигуры и поверхности будем понимать площадь S, для линии – длину линии, для пространственного тела объём.
Определённый
интеграл по фигуре Ω от заданной на ней
функции f(p)
называется предел n-интегральной суммы,
когда
.
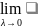В случае когда фигура плоск. обл.Д,
интеграл называется двойным.
2 Масса фигуры переменной плотности
. Масса фигуры (отрезка, дуги, плоской фигуры, части криволинейной поверхности, тела)
,
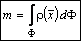если
подынтегральная функция 
, 
,
задает
плотность 
линейная 
распределения поверхностная
(
)
массы
по 
объемная
(
)
в
зависимости от размерности
фигуры, 
,
, 
на
.
3 Геометрический смысл ди (двойного интеграла)
Вычислим V цилиндрического тела. Сверху ограниченного поверхностью z=f(x,y) проекция поверхности на плоскость xoy =>область Д и цилиндр. образующ. кот. // oz
Р
азобьем
область Д на n-цилиндрических
тел основаниями которых будут элементы
области ∆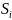
.
Возьмём произвольную точку
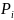в области ∆
и h-z=f (
),
тогда ∆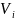
=f(
)*
∆
,
a
V
≈
=>
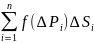V=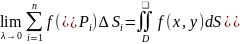
Двойной интеграл – V цилиндрического тела с основанием Д ограниченного сверху поверхностью z=f(x,y)
Замечания:
1. Если объём ограниченный сверху
z=f(x,y),
снизу z=f1(x,y),
то V=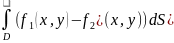
2.
Если f(x,y)≤0
неопред. в области Д, то ДИ от этой функции
= V цилиндрического тела взятому со
знаком «-»
4 Геометрический смысл Кр и -1
1. Дугу
кривой |
|
или 
в
пространстве XOYZ разбиваем
на nмалых
частей точками M0=A, M1,…,Mn=B;
обозначаем длины хорд 
, (Рис.
13)
2. Вычисляем
значения функции f (x,y,z)
в произвольно выбираемых точках 
на i-той
части разбиения и умножаем их на
соответствующие длины хорд Δli:
, 
3. Составляем интегральную сумму
и
вычисляем её предел при λ → 0, где 
–
это ранг разбиения.
4. Если
предел интегральной суммы существует,
является конечным и не зависит ни от
способа разбиения дуги (l)
на элементарные части, ни от выбора на
них точек 
,
то он называется криволинейным
интегралом I рода от функции
f (x, y, z) по линии l:
|
5 Свойства определённого интеграла по фигуре
пусть
функция f(p) 
непрерывна
на фигуре Ф т.е. ОИ по фигуре Ф существует,
тогда выполняются следующие свойства:
1. 
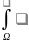f1(p)∓f2pdw=
f1pdw∓
f2pdw
2. kf(p)dw=k f(p)dw
3. если фигуру Ф разбить на конечное число частей, то интеграл равен сумме частей интегралов.
4. если dw=w ,
то 
dl=l ,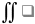 
ds=s,d
σ=σ,
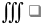dv=v
5. если f1(p)<f2(p), то f1pdw< f2pdw
6. /f(p)dw/≤ /f(p)/dw
7. оценка интеграла по фигуре. Если m и M наибольшее и наименьшее значение функции f(p) на фигуре Ф, то mw≤ f(p)dw≤Mw
8. (о среднем значении) если функция f(p) непрерывна на Ф с
мерой w, то найдется точка Р∈Ф, то f(p)dw= (Po)w