21 Формула Остроградского-Гаусса

Теорема: Если функции Q(x,y,z); P(x,y,z); R(x;y;z) непрерывны вместе со своими частными производными 1-ого порядка в области V, то имеет место формула:

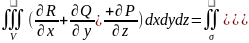
Интегрирование производится по внешней стороне поверхности.

22. Скалярное поле. Линии и поверхности уровня скалярного поля. Производная по направлению.

Скалярное поле. Если каждой точке  пространства ставится в соответствие скалярная величина  , то возникает скалярное поле (например, поле температуры, поле электрического потенциала). Если введены декартовы координаты, то обозначают также

  или        . Поле может быть плоским, если    , центральным (сферическим), если    , цилиндрическим, если  .

 

Поверхности и линии уровня. Свойства скалярных полей можно наглядно изучать с помощью поверхностей уровня. Это поверхности в пространстве, на которых   принимает постоянное значение. Их уравнение:   . В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение:    . В отдельных случаях линии уровня могут вырождаться в точки, а поверхности уровня в точки и кривые.

 

ПРИМЕР 1.  Исследование скалярного поля с помощью линий уровня.

Производная по направлению и градиент скалярного поля. Пусть    - единичный вектор с координатами   ,   - скалярное поле. Производная по направлению характеризует изменение поля в данном направлении и вычисляется по формуле 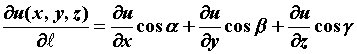  . Производная по направлению представляет собой скалярное произведение вектора    и вектора с координатами   , который называется градиентом функции   и обозначается   . Поскольку   , где   - угол между    и   , то вектор   указывает   направление скорейшего возрастания поля  , а его модуль равен производной по этому направлению. Так как компоненты градиента являются частными производными, нетрудно получить следующие свойства градиента:

23 Градиент, свойства градиента

Пусть дана функция . U=f(x,y,z) определенная и дифференцируема в некоторой области Д.

Градиентом функции наз вектор проекции которого на оси координат равны соответствующим частным производным.

grad U=(∂U/∂х)i+(∂U/∂у)j+(∂U/∂z)k

Своиства градиента: 1. Производная по направлению имеет МАХ значение в направлении совпадающем с градиентом.

1. Производная в направлении ⊥ градиенту равно 0.

2. Градиент ⊥ линиям уровня.

3. Док-во: U=u(x,y) тогда gradU=UX1i+UX1j  тогда угловой коэф прямой совпад с градиентом будет равен. К1=tgα=(UY1/UX1)

4. Линией уровня наз линия на к-ой функция принимает постоянное значение u(x,y)=с.  Геометрический смысл градиента состоит в том что градиент указывает направление наибольшего изменения фун.

24 Векторное поле, определение, векторные линии, труба

Векторное поле. Если каждой точке  пространства ставится в соответствие вектор  , то говорят, что задано векторное поле (поле скоростей частиц движущейся жидкости, силовое поле, поле электрической напряженности). В декартовой системе координат векторное поле можно записать в виде:  . Скалярные функции  однозначно определяют векторное поле. Векторное поле может быть плоским, если  , сферическим, когда  ,  , цилиндрическим, когда  ,  .

 

ПРИМЕР 1.  Исследование плоского векторного поля.

 

Векторные линии (линии тока). Для наглядного представления векторных полей используют векторные линии (линии тока). Это кривые, в каждой точке которых вектор  является касательным вектором. Через каждую точку  проходит одна линия тока. За исключением точек, где поле не определено или  , линии тока никогда не пересекаются. В декартовых координатах дифференциальные уравнения линий тока имеют вид: 

Векторная трубка

Пусть   — векторное поле, S — какая-нибудь площадка на этом поле. Проведём через границу этой площадки векторные линии. Образуемая при этом фигура называется векторной трубкой (при этом векторные линии, проходящие через S, целиком лежат внутри векторной трубки).