
- •Определение и свойства двойного интреграла.
- •3 Вычисление двойного интеграла в полярных координатах
- •5 Вычисление объёмов тел площадей плоских фигур с помощью двойного интеграла.
- •7.Механические приложения двойного интеграла.
- •8 Вычисление и свойство тройного интеграла.
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •Основные свойства тройного интеграла
- •9.Вычисление тройного интегралав декартовых координатах
- •10 Цилиндрические координаты.Тройной интеграл в цилиндрических координатах. Замена переменной в тройном интеграле
- •11.Сферические координаты. Тройной интеграл сферических координатах
- •12.Механические приложения тройного интеграла.
- •13. Криволинейный интеграл I рода. Основные свойства кри-I.
- •2.1. Криволинейный интеграл I рода (кри-I)
- •10. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •2.2. Вычисления криволинейного интеграла I рода
- •16. Приложения кри-I кри-2.
- •14. Криволинейный интеграл II рода. Основные свойства кри-II.
- •Криволинейный интеграл II рода (кри-II)
- •15. Формула Остроградского – Грина.
- •II способ
- •17.Поверхностный интеграл I рода
- •3.1. Поверхностный интеграл I рода
- •3.2. Вычисление поверхностного интеграла I рода
- •18.Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •3.3. Поверхностный интеграл II рода
- •II способ
- •III способ
- •21. Понятие скалярного поля. Поверхности и линии уровня.
- •4.1. Скалярное поле
- •22.Производная по направлению. Градиент. Производная по направлению
- •Градиент
- •25. Поток и дивергенция векторного поля.
- •24. Циркуляция и ротор векторного поля.
- •4.5. Циркуляция поля
- •4.6. Ротор поля. Формула Стокса
- •27. Потенциальные, соленоидальные и гармонические векторные поля.
- •Потенциальное векторное поле
- •Гармоническое векторное поле
- •28.Понятие числового ряда и его суммы.Сходящиеся и расходящиеся ряды.Свойства
- •5.1. Основные понятия
- •29. Сформулировать и доказать необходимый признак сходимости ряда. Достаточный признак расходимости ряда. Гармонический ряд.
- •5.2. Необходимый признак сходимости ряда
- •5.3. Достаточные признаки сходимости ряда
- •31. Признаки сравнения рядов. Признаки сравнения рядов.
- •32. Признак ДаламбераПризнак Даламбера
- •33. Радикальный признак Коши. Радикальный признак Коши
- •30.Интегральный признак Коши.
- •35. Знакочередующиеся ряды. Признак Лейбница.
- •34. Знакопеременные ряды.Абсолютная и условная сходимости рядов
- •Абсолютная и условная сходимости рядов
- •36. Функциональный ряд. Точка сходимости. Область сходимости функциональног
- •7.1. Функциональные ряды
- •37. Степенной ряд. Сформулировать и доказать теорему Абеля.
- •38 Свойства степенных рядов Свойства степенных рядов
- •39. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •Разложение функций в степенной ряд
22.Производная по направлению. Градиент. Производная по направлению
Пусть
задано скалярное поле, т.е. задана функция
 ,
и точка
,
и точка
 .
Будем предполагать, что функция
непрерывна и имеет непрерывные производные
по своим аргументам в области
.
.
Будем предполагать, что функция
непрерывна и имеет непрерывные производные
по своим аргументам в области
.
Определение 4.3.
Производной
от функции
в точке
по направлению вектора
 называется предел отношения
называется предел отношения
 при
при
 ,
т.е.
,
т.е.
 .
.
Если функция
дифференцируемая, то производная от
функции в точке
 по направлению вектора
находится по следующей формуле:
по направлению вектора
находится по следующей формуле:
 ,
(4.1)
,
(4.1)
где

направляющие косинусы вектора
.
направляющие косинусы вектора
.
В случае функции
двух переменных
 ,
т.е. когда поле плоское, формула (4.1)
примет следующий вид:
,
т.е. когда поле плоское, формула (4.1)
примет следующий вид:
 ,
(4.2)
,
(4.2)
где
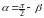 .
.
Подобно тому, как
частные производные
 характеризуют скорость изменения
функции
в направлении осей координат, так и
производная по направлению
характеризуют скорость изменения
функции
в направлении осей координат, так и
производная по направлению
 будет являться скоростью
изменения функции
в
точке
по направлению вектора
.
Если
будет являться скоростью
изменения функции
в
точке
по направлению вектора
.
Если
 ,
то функция
возрастает
в направлении
,
если
,
то функция
возрастает
в направлении
,
если
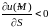 ,
то функция
убывает
в направлении
.
,
то функция
убывает
в направлении
.
Градиент
В каждой точке
области
,
в которой задана скалярная функция
 ,
определим вектор, проекциями которого
на оси координат являются значения
частных производных
в выбранной точке
.
Назовем этот вектор градиентом
функции
и обозначим его символами
,
определим вектор, проекциями которого
на оси координат являются значения
частных производных
в выбранной точке
.
Назовем этот вектор градиентом
функции
и обозначим его символами
 или
или
 (набла-оператор, записываемый в виде
«вектора» с компонентами
(набла-оператор, записываемый в виде
«вектора» с компонентами ).
).
Определение 4.4. Градиентом функции в точке называется вектор, проекции которого служат значения частных производных этой функции, т.е.
 .
(4.3)
.
(4.3)
Подчеркнем, что
проекции градиента зависят от выбора
точки
и изменяются с изменением координат
этой точки. Таким образом, каждой точке
скалярного поля, определяемого функцией
,
соответствует определенный вектор –
градиент этой функции. Отметим, что
градиент линейной функции
 есть постоянный вектор
есть постоянный вектор
 .
.

Учитывая то, что скалярное произведение равно модулю одного вектора умноженному на проекцию другого вектора на направление первого, то можно еще сказать, что: производная функции по данному направлению равна проекции градиента функции на направление дифференцирования, т.е.
 ,
,
где
угол между
и направлением
.Свойства
:1) Производная
в данной точке по направлению вектора
имеет наибольшее значение, если
направление вектора
совпадает с направлением градиента,
когда
 ,
т.е. при
,
т.е. при
 ;
это наибольшее значение производной
равно
;
это наибольшее значение производной
равно
 .
.
Таким образом, направление градиента есть направление наискорейшего возрастания функции. В противоположном направлении функция будет быстрее всего убывать. наибольшая скорость изменения функции в точке .
2) Производная по направлению вектора, перпендикулярного к вектору , равна нулю.
3) Градиент функции в каждой точке направлен по нормали к поверхности уровня скалярного поля, проходящего через эту точку.
4)
 .
.
5)
 ,
где
,
где
 .
.
6)
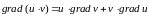 и др.
и др.
Пример 4.2.
Дана функция
 .
Найти:
.
Найти:
1)
производную в точке
 по направлению к точке
по направлению к точке
 ;
;
2) наибольшую скорость возрастания функции в точке .
Решение.
1) Находим координаты и направляющие
косинусы вектора
 :
:
 ;
;
 .
.
Находим частные производные и значения частных производных в точке :
 ;
;
 ;
;
 .
.
Тогда по формуле (4.1) получаем:
 .
.
Так как
 ,
то в данном направлении функция убывает.
,
то в данном направлении функция убывает.
2) Используя формулу (4.3) запишем градиент функции в точке :
 .
.
Находим наибольшую скорость возрастания функции в точке :
 .
.
23.Понятие векторного поля. Векторные (силовые) линии. Векторная трубка.Определение 4.5. Если каждой точке области соответствует некоторый вектор , то говорят, что задано векторное поле или векторная функция точки.
Вектор
,
определяющий векторное поле, можно
рассматривать как векторную функцию
трех скалярных аргументов
,
т.е.
 .
.
Вектор можно представить, разложив его по ортам координатных осей, в виде:
 ,
,
где

проекции вектора
на оси координат, а также скалярные
функции, которые непрерывны со своими
частными производными.
проекции вектора
на оси координат, а также скалярные
функции, которые непрерывны со своими
частными производными.
Простейшими геометрическими характеристиками векторного поля являются векторные линии.
Определение 4.6. Векторной (силовой) линией поля называется линия, касательная к которой в каждой точке имеет направление соответствующего ей вектора
Определение 4.7. Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Изучение векторного поля обычно начинается с изучения расположения его векторных линий. Векторные линии поля
описываются системой дифференциальных уравнений
 .
(4.4)
.
(4.4)
Пример 4.3.
Найти векторную линию векторного поля
 ,
проходящую через точку
,
проходящую через точку
 .
.
Решение. Согласно формуле (4.4) получаем систему дифференциальных уравнений
 .
.
Решаем первое уравнение:



 .
.
или,
в параметрическом виде:
 .
.
Решаем второе уравнение:



 .
.
Так как векторная
линия должна проходить через точку
,
то легко находим, что постоянные
интегрирования
 .
.
Уравнения векторной
линии данного векторного поля имеют
вид:

 ,
,

это винтовая линия.
это винтовая линия.
Векторное
поле, порожденное градиентом скалярного
поля
 (или
(или
 ),
называется полем
градиента.
Векторные линии
),
называется полем
градиента.
Векторные линии
 (или
(или
 )
это кривые, вдоль которых функция
(или
)
максимально возрастает (убывает). Эти
линии всегда ортогональны к поверхностям
(или линиям) уровня скалярного поля
(или
)
это кривые, вдоль которых функция
(или
)
максимально возрастает (убывает). Эти
линии всегда ортогональны к поверхностям
(или линиям) уровня скалярного поля
(или
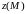 ).
).
Дифференциальные уравнения для определения векторных линий имеют вид:
 .
.
