
- •Определение и свойства двойного интреграла.
- •3 Вычисление двойного интеграла в полярных координатах
- •5 Вычисление объёмов тел площадей плоских фигур с помощью двойного интеграла.
- •7.Механические приложения двойного интеграла.
- •8 Вычисление и свойство тройного интеграла.
- •1) Разбиваем область на «элементарных областей» .
- •3) Возьмем произвольную точку .
- •5) Составляем интегральную сумму
- •Основные свойства тройного интеграла
- •9.Вычисление тройного интегралав декартовых координатах
- •10 Цилиндрические координаты.Тройной интеграл в цилиндрических координатах. Замена переменной в тройном интеграле
- •11.Сферические координаты. Тройной интеграл сферических координатах
- •12.Механические приложения тройного интеграла.
- •13. Криволинейный интеграл I рода. Основные свойства кри-I.
- •2.1. Криволинейный интеграл I рода (кри-I)
- •10. Вычисление криволинейного интеграла I рода: явное представление кривой, параметрическое представление кривой, полярное представление кривой.
- •2.2. Вычисления криволинейного интеграла I рода
- •16. Приложения кри-I кри-2.
- •14. Криволинейный интеграл II рода. Основные свойства кри-II.
- •Криволинейный интеграл II рода (кри-II)
- •15. Формула Остроградского – Грина.
- •II способ
- •17.Поверхностный интеграл I рода
- •3.1. Поверхностный интеграл I рода
- •3.2. Вычисление поверхностного интеграла I рода
- •18.Поверхностный интеграл II рода. Свойства поверхностного интеграла II рода.
- •3.3. Поверхностный интеграл II рода
- •II способ
- •III способ
- •21. Понятие скалярного поля. Поверхности и линии уровня.
- •4.1. Скалярное поле
- •22.Производная по направлению. Градиент. Производная по направлению
- •Градиент
- •25. Поток и дивергенция векторного поля.
- •24. Циркуляция и ротор векторного поля.
- •4.5. Циркуляция поля
- •4.6. Ротор поля. Формула Стокса
- •27. Потенциальные, соленоидальные и гармонические векторные поля.
- •Потенциальное векторное поле
- •Гармоническое векторное поле
- •28.Понятие числового ряда и его суммы.Сходящиеся и расходящиеся ряды.Свойства
- •5.1. Основные понятия
- •29. Сформулировать и доказать необходимый признак сходимости ряда. Достаточный признак расходимости ряда. Гармонический ряд.
- •5.2. Необходимый признак сходимости ряда
- •5.3. Достаточные признаки сходимости ряда
- •31. Признаки сравнения рядов. Признаки сравнения рядов.
- •32. Признак ДаламбераПризнак Даламбера
- •33. Радикальный признак Коши. Радикальный признак Коши
- •30.Интегральный признак Коши.
- •35. Знакочередующиеся ряды. Признак Лейбница.
- •34. Знакопеременные ряды.Абсолютная и условная сходимости рядов
- •Абсолютная и условная сходимости рядов
- •36. Функциональный ряд. Точка сходимости. Область сходимости функциональног
- •7.1. Функциональные ряды
- •37. Степенной ряд. Сформулировать и доказать теорему Абеля.
- •38 Свойства степенных рядов Свойства степенных рядов
- •39. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд.
- •Разложение функций в степенной ряд
Определение и свойства двойного интреграла.
Рассмотрим
в плоскости
 замкнутую
область
замкнутую
область
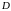 .
Область
называется замкнутой, если она ограничена
замкнутой линией, и точки, лежащие на
границе, считаются принадлежащими
области
.
.
Область
называется замкнутой, если она ограничена
замкнутой линией, и точки, лежащие на
границе, считаются принадлежащими
области
.
Пусть
в области
задана непрерывная функция
 .
.

1)
Разбиваем область
на
 «элементарных областей»
«элементарных областей»
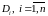 .
.
2)
Площадь области
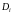 обозначим
обозначим
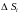 ,
а диаметр (наибольшее расстояние между
двумя точками области) – через
,
а диаметр (наибольшее расстояние между
двумя точками области) – через
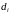 .
.
3)
Возьмем произвольную точку
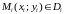 .
.
4)
Находим
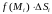 ,
что равно объему тела (призма), площадь
основания которого
,
а высота равна
,
что равно объему тела (призма), площадь
основания которого
,
а высота равна
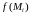 .
.
5) Составляем интегральную сумму
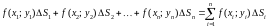 .
.
6)
Обозначим через
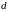 длину наибольшего из диаметров
«элементарных областей», т.е.
длину наибольшего из диаметров
«элементарных областей», т.е.
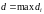 ,
,
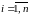 .
Найдем предел интегральной суммы, когда
.
Найдем предел интегральной суммы, когда
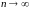 так, что
так, что
 .
Если предел существует и не зависит от
способа разбиения области
на части, ни от выбора точек в них, то он
называется двойным
интегралом
от функции
по области
.
.
Если предел существует и не зависит от
способа разбиения области
на части, ни от выбора точек в них, то он
называется двойным
интегралом
от функции
по области
.
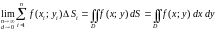 .
.
Таким
образом, двойным
интегралом от
по замкнутой областью
называется предел интегральной суммы
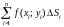 ,
когда число «элементарных областей»
неограниченно возрастает, а длина
наибольшего диаметра стремится к нулю:
,
когда число «элементарных областей»
неограниченно возрастает, а длина
наибольшего диаметра стремится к нулю:
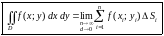 .
(1.1)
.
(1.1)
интегрируемая
функция
в области
;
область
интегрирования; и
и
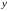
переменные
интегрирования
dx
dy
или dS
элемент
площади.
переменные
интегрирования
dx
dy
или dS
элемент
площади.
Основные свойства двойного интеграла
Свойства двойного интеграла аналогичны свойствам определенного интеграла функции одной переменной на отрезке. Поэтому перечислим основные свойства двойного интеграла (без доказательства), считая подынтегральные функции интегрируемыми.
1.
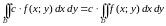 ,
где
,
где
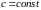 .
.
2.
 .
.
3.
Если область
разбить линией на две области
 и
и
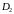 такие, что
такие, что
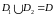 ,
а пересечение
,
а пересечение
 ,
где
,
где
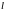
линия, разделяющая
и
(см. рисунок), то
линия, разделяющая
и
(см. рисунок), то

4.
Если в области
имеет место неравенство
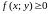 ,
то и
,
то и
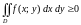 .
.
5.
Если в области
функции
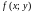 и
и
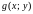 удовлетворяют неравенству
удовлетворяют неравенству
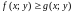 ,
то и
,
то и
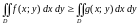 .
.
6.
Если
 ,
,
 ,
то
,
то
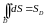 ,
где
,
где
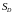
площадь области интегрирования
.
площадь области интегрирования
.
7.
Если функция
непрерывна в замкнутой области
,
площадь которой
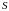 ,
то
,
то
 ,
,
где
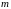 и
и
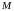
соответственно наименьшее и наибольшее
значения подынтегральной функции в
области
.
соответственно наименьшее и наибольшее
значения подынтегральной функции в
области
.
8.
Если функция
непрерывна в замкнутой области
,
площадь которой
,
то в этой области существует такая точка
 ,
что
,
что
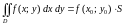 .
.
Величину
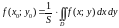 называют средним
значением
функции
в области
.
называют средним
значением
функции
в области
.
2Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть
требуется вычислить двойной интеграл
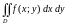 ,
где функция
непрерывна в области
.
Тогда, двойной интеграл выражает объем
цилиндрического тела, ограниченного
сверху поверхностью
.
Найдем этот объем, используя метод
параллельных сечений. Ранее было
показано, что
,
где функция
непрерывна в области
.
Тогда, двойной интеграл выражает объем
цилиндрического тела, ограниченного
сверху поверхностью
.
Найдем этот объем, используя метод
параллельных сечений. Ранее было
показано, что
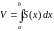 ,
где
,
где

площадь сечения плоскостью, перпендикулярной
оси
площадь сечения плоскостью, перпендикулярной
оси
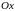 ,
а
,
а
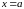 и
и
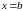
уравнения плоскостей, ограничивающих
данное тело.
уравнения плоскостей, ограничивающих
данное тело.
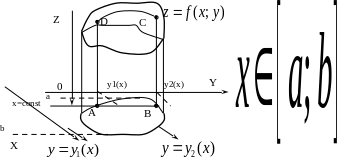
направлении
оси
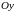 :
любая прямая, параллельная оси
,
пересекает границу области не более
чем в дух точках.
:
любая прямая, параллельная оси
,
пересекает границу области не более
чем в дух точках.
Построим
сечение цилиндрического тела плоскостью,
перпендикулярной оси
:
 ,
где
,
где
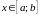 .
.
В
сечении получаем криволинейную трапецию
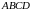 ,
ограниченную линиями
,
где
,
,
ограниченную линиями
,
где
,
 и
и
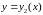 .
Площадь
этой трапеции находим с помощью
определенного интеграла:
.
Площадь
этой трапеции находим с помощью
определенного интеграла:
 .
.
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
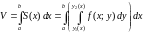 .
.
С другой стороны, объем цилиндрического тела определяется как двойной интеграл от функции по области . Следовательно,
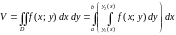 .
.
Таким образом, для вычисления двойного интеграла функции по области используется следующая формула
 .
(1.2)
.
(1.2)
Правую
часть (1.2) называют двукратным
(или повторным)
интегралом
от функции
по области
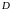 .
Интеграл
.
Интеграл
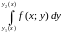 называется внутренним
интегралом.
называется внутренним
интегралом.
Для
вычисления двукратного интеграла
сначала берем внутренний интеграл,
считая
постоянным, затем берем внешний интеграл,
т.е. результат первого интегрирования
интегрируем по
в пределах от
 до
до
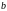 .
.
Если
область
ограничена прямыми
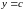 и
и
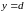 (
(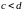 ),
кривыми
),
кривыми
 и
и
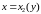 ,
причем
,
причем
 для всех
для всех
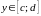 ,
т.е. область
правильная
(стандартная) в направлении оси
,
то, рассекая тело плоскостью
,
т.е. область
правильная
(стандартная) в направлении оси
,
то, рассекая тело плоскостью
 ,
аналогично получаем
,
аналогично получаем
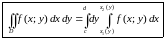 .
(1.3)
.
(1.3)
Здесь при вычислении внутреннего интеграла, считаем постоянным.
Замечания.
1.
Формулы (1.2) и (1.3) справедливы и в случае,
когда
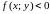 ,
,
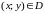 .
.
2. Если область правильная в обоих направлениях, то двойной интеграл можно вычислять как и по формуле (1.2), так и по формуле (1.3).
3. Если область не является правильной ни «по », ни «по », то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси или оси .
4. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример
1.1. Вычислить
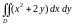 ,
если область
ограничена линиями:
,
если область
ограничена линиями:
 .
.
Решение. I способ.
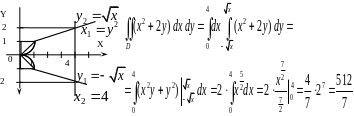
II способ. Построенная область является правильной в направлении оси . Для вычисления двойного интеграла воспользуемся формулой (1.3):

 .
.
