70 Спецификация моделей со случайными возмущениями и преобразование их к системе нормальных уравнений
Один из принципов спецификации - включение в спецификацию экономической модели случайных возмущений. На практике не всегда удается учесть влияние всех факторов на изучаемую переменную (например, в функции спроса учесть возрастные особенности потребителя), выбрать правильную форму математической зависимости между экономическими переменными (например, нелинейную вместо линейной), безошибочно выполнить измерения (правильно провести опрос). Поэтому эндогенные переменные модели следует рассматривать как случайные величины и, помимо детерминированной составляющей, описывающей поведение эндогенной переменной в зависимости от предопределенных переменных, включать некоторые случайные величины, называемые случайные возмущения.
Y = f(x)+Ɛ , где f(x)- часть эндогенной переменной, объясняемая значением экзогенной переменной Х; ε – случайное возмущение. Для того чтобы среди множества уравнений регрессии выбрать одно, необходим критерий отбора. При оценивании параметров регрессионных моделей наиболее часто применяется МНК. Его оценки обладают свойствами несмещённости, состоятельности, эффективности:
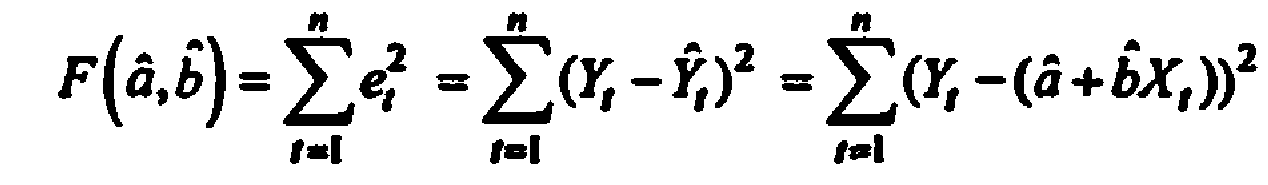(1)
То есть оценки параметров должны быть подобраны таким образом, чтобы сумма квадратов случайных возмущений стремилась к минимуму
(2)
Для нахождения минимума дифференцируем (1):
Получаем стандартную форму нормальных уравнений:
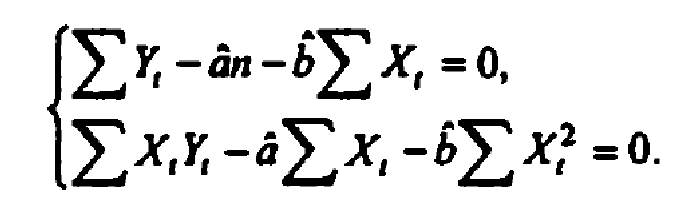
Из которых находим параметры.
71.Способы корректировки гетероскедастичности. Метод взвешенных наименьших квадратов.
Одним
из основных способов корректировки
гетероскедастичности является
использование метода взвешенных
наименьших квадратов. Он применяется
в том случае, когда известны диагональные
элементы автоковариационной матрицы
вектора возмущений
.
В этом случае уравнения наблюдений
можно преобразовать следующим образом.
Поделим каждый член на СКО возмущения:
,
где t=1….n.
В результате преобразования спецификация
принимает вид спецификации классической
регрессионной модели:
. Определим количественные характеристики
случайного возмущения
:
математическое
ожидание: E{
}=E{
}=
=0
дисперсия
случайного члена: Var
{
}=Var{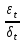
}=
=
=1,
таким образом
~N(0,1)
и при помощи данного преобразования
случайное возмущение приобрело свойство
гомоскедастичности.
В
случае, если значения
неизвестны, используется доступный
обобщенный метод наименьших квадратов.
В этом методе выполняется оценка
неизвестных дисперсий, но при условии,
что на структуру автоковариационной
матрицы накладываются дополнительные
ограничения (предпосылки). Наиболее
часто используется следующая предпосылка:
СКО возмущения пропорционально одному
из регрессоров.
72.Статистические свойства оценок параметров парной регрессионной модели.
Теорема
Гаусса-Маркова. Пусть матрица Х имеет
полный ранг. При выполнении условий
Гаусса-Маркова МНК-оценки параметров
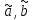относятся к классу линейных по Y,
несмещенных оценок с минимальной
дисперсией. Покажем линейность оценок
следующим выражением:
Докажем несмещенность полученных
оценок. Введем обозначение: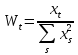
, тогда можно показать, что справедливы
следующие соотношения:
,
,
,
.
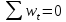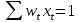Свойство несмещенности оценок параметра
проверяется соответственно:
,
,
E(
)=b
,
E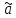
=a.
Оценка является состоятельной если:
,
т.е с увеличением объема выборки оценки
более плотно концентрируются около
истинного значения. Оценка становится
более надежной в вероятностном смысле,
и дисперсия оценки стремится к нулю.
Для доказательства состоятельности
оценок параметров парной регрессии
получим выражения для элементов
автоковариационной матрицы вектора
оценок параметров
.
В матричной форме
=AY,
поэтому
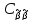=Cov{AY,AY}=
.
Определим элементы автоковариационной
матрицы случайного вектора Y:
,
где
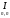-единичная
матрица с размером nxn.
Таким образом
=
=(
Так как Q=
,
получим выражения элементов ковариационной
матрицы вектора
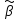через выборочные данные:
,
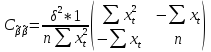таким образом имеем:
,
.
Как следует из этих выражений, с
увеличением объема выборки n
дисперсии несмещенных оценок параметров
стремятся к нулю, то есть МНК-оценки
параметров парной регрессии являются
состоятельными.
В
качестве эффективности оценок чаще
всего используется критерий вида:
Е{
}=
.
Несмещенная оценка является эффективной,
если она имеет минимальную дисперсию
по сравнению с любыми другими оценками
этого параметра в классе выбранных
процедур(т.е. является менее случайной).
Доказательство эффективности МНК-оценок
выполняется
путем сравнения их дисперсий с дисперсиями
линейных несмещенных оценок
.
Пусть
-вектор
несмещенных линейных оценок параметров
,
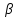определяемых выражением вида
,
где С- произвольная(2хn)-
матрица. Тогда в силу несмещенности
оценки
и равенства AX=
,
можно записать:
,
откуда следует, что CX=0.
Определим автоковариационную матрицу
вектора оценок
:
,
так как Cov{Y,Y}=
I и С
=0,
A
=
.
Диагональные элементы автоковариационной
матрицы-дисперсии оценок параметров.
Диагональные элементы
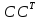неотрицательны, поэтому Var(
Var(
,
т.е МНК-оценка
является эффективной, имея минимальную
дисперсию по сравнению с любыми
несмещенными оценками неизвестного
параметра в классе линейных процедур