
- •1. Определение матрицы. Виды матриц. Равенство матриц.
- •2. Линейные и нелинейные операции над матрицами
- •Умножение матриц. Свойства произведения матриц
- •3. Перестановка чисел, число инверсий, определитель
- •4.Минор к-порядка минор элемента матрицы, ранг
- •Метод окаймляющих миноров:
- •Инвариантность ранга матрицы относительно элементарных преобразований.
- •Критерий существования обратной матрицы
- •Фундаментальной системой решений (фср), системы однородных линейных уравнений называется совокупность решений, которая обладает двумя свойствами:
- •Определение проекции вектора на ось:
- •Направляющие косинусы в декартовой системе координат
- •Линейная зависимость и независимость свободных векторов:
- •Критерий линейно зависимости свободных векторов
- •Определение базиса:
- •Теорема о базисе
- •Скалярное произведение векторов
- •Критерий линейной зависимости векторов линейного пространства
- •Параметрическое уравнение.
- •Уравнение плоскости проходящей через точку параллельно 2м коллинеарным векторам
- •Уравнение прямой проходящей через точку параллельно вектору
- •Каноническое уравнение прямой в пространстве
- •Взаимное расположение прямой и плоскости в пространстве
- •Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость .
- •Эллипс, свойства эллипса
- •Метод параллельных сечений исследования формы поверхности.
Уравнение плоскости проходящей через точку параллельно 2м коллинеарным векторам
Составим уравнение
плоскости, проходящей через
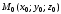 ,
параллельно неколлинеарным векторам
,
параллельно неколлинеарным векторам
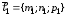 и
и
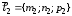 .
.
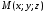 – текущая точка
плоскости.
– текущая точка
плоскости.
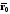 и
и
 – радиус-векторы точек
– радиус-векторы точек
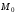 и
и
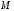 .
Рассмотрим
.
Рассмотрим
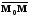
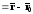 ,
,
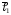 и
и
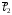 .
По условию они компланарны. Следовательно
.
По условию они компланарны. Следовательно
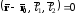 ,
,
в
координатной форме,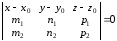 .
.
Полученные уравнения называют уравнениями плоскости, проходящей через точку параллельно двум неколлинеарным векторам
Уравнение плоскости проходящей через 3 заданные точки
пусть плоскость
проходит через
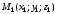 ,
,
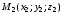 и
и
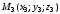 ,
не лежащие на одной прямой. Тогда векторы
,
не лежащие на одной прямой. Тогда векторы
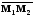
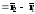
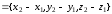
и
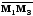
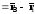

неколлинеарные и параллельны плоскости. Следовательно, уравнение этой плоскости будет иметь вид
 ,
в координатной форме:
,
в координатной форме: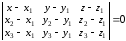 .
.
Данные уравнения
называют уравнениями плоскости,
проходящей через три точки
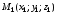 ,
,
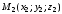 и
и
 .
.
Прямая линия в пространстве
Пусть
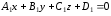 и
и
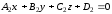 – уравнения непараллельных плоскостей.
Тогда эти плоскости пересекаются по
некоторой прямой
– уравнения непараллельных плоскостей.
Тогда эти плоскости пересекаются по
некоторой прямой
 .
Координаты любой точки прямой
.
Координаты любой точки прямой
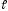 удовлетворяют одновременно обоим
уравнениям, т.е. являются решениями
системы
удовлетворяют одновременно обоим
уравнениям, т.е. являются решениями
системы
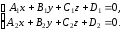
Данную систему называют общими уравнениями прямой в пространстве
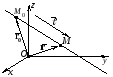
Уравнение прямой проходящей через точку параллельно вектору
Даны ,
и
,
и
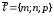 .
Вектор l
называют направляющим
вектором
этой прямой.
.
Вектор l
называют направляющим
вектором
этой прямой.
 – текущая точка прямой.
– текущая точка прямой.
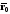 и
и
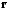 – радиус-векторы точек
– радиус-векторы точек
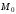 и
и
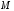 .
.
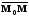
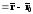
 .
Следовательно, существует такое число
.
Следовательно, существует такое число
 (
(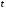 называют параметром),
что
называют параметром),
что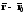
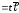 ,⇒
,⇒
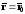
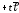 ,
,
или,
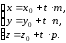 (48)
(48)
полученную систему называют параметрическими уравнениями прямой в пространстве.
Каноническое уравнение прямой в пространстве
Если вектор
 не параллелен ни одной из координатных
плоскостей то из уравнений системы
можно выразить параметр
не параллелен ни одной из координатных
плоскостей то из уравнений системы
можно выразить параметр
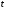 :
:
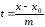 ,
,
 ,
,
 и заменить систему одним уравнением
вида:
и заменить систему одним уравнением
вида:
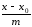
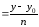
 ,
,
Канонические и параметрические уравнение прямой через 2 точки
Даны
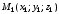 и
и
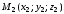 .
Тогда вектор
.
Тогда вектор
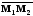

является
ее направляющим вектором и канонические
уравнения этой прямой будут иметь вид
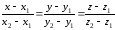 .
.
Взаимное расположение прямой и плоскости в пространстве
Пусть
в пространстве заданы плоскость
 и прямая
и прямая
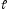 .
Они могут быть
.
Они могут быть
1) параллельны; 2) прямая может лежать в плоскости; 3) прямая и плоскость могут пересекаться в одной точке.
Пусть
 :
: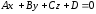 и
и
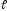 :
: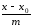

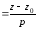 .
Тогда
.
Тогда
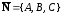 – нормальный вектор плоскости,
– нормальный вектор плоскости,
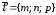 – направляющий вектор прямой.
– направляющий вектор прямой. 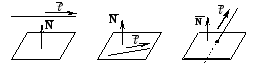
Если плоскость и
прямая параллельны или прямая
 целиком лежит в плоскости
целиком лежит в плоскости
 ,
то векторы
,
то векторы
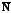 и
и
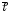 – перпендикулярны. Следовательно
– перпендикулярны. Следовательно
 ,
или
,
или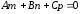 .
.
Если данные условия не выполняются, то прямая и плоскость пересекаются в одной точке.
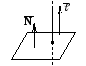
Если

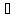 l . В этом случае
l . В этом случае
 и
и
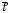 будут параллельны, т.е.
будут параллельны, т.е.
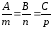 .
.
Пусть прямая
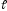 лежит в плоскости
лежит в плоскости
 .
Тогда любая точка прямой лежит в
плоскости и, следовательно, ее координаты
удовлетворяют уравнению плоскости. В
частности,
.
Тогда любая точка прямой лежит в
плоскости и, следовательно, ее координаты
удовлетворяют уравнению плоскости. В
частности,
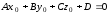 ,
где
,
где
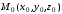 – некоторая точка прямой
– некоторая точка прямой
 .
Если же прямая параллельна плоскости,
то она не имеет общих точек с плоскостью
и, =>
.
Если же прямая параллельна плоскости,
то она не имеет общих точек с плоскостью
и, =>
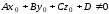 .
.
Таким образом,
если прямая лежит в плоскости, то должны
выполняться два условия:
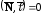 и
и
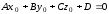 ;
;
если
прямая параллельна плоскости, то
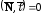 и
и
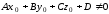 ,
,
где
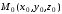 – точка прямой
– точка прямой
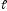 .
.
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость .
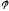 – угол между прямой
– угол между прямой
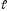 и плоскостью
и плоскостью
 .
Через точку пересечения прямой
.
Через точку пересечения прямой
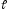 плоскости
плоскости
 проведем прямую
проведем прямую
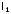 ,
,
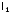
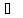
 .
Пусть
.
Пусть
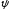 – острый угол между прямыми
– острый угол между прямыми
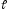 и
и
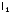 .
.
Тогда
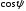
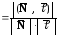 .
Но
.
Но 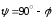 ,
,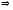
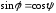
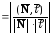 –
формула для определения угла между
прямой и плоскостью.
–
формула для определения угла между
прямой и плоскостью.
