
- •1. Определение матрицы. Виды матриц. Равенство матриц.
- •2. Линейные и нелинейные операции над матрицами
- •Умножение матриц. Свойства произведения матриц
- •3. Перестановка чисел, число инверсий, определитель
- •4.Минор к-порядка минор элемента матрицы, ранг
- •Метод окаймляющих миноров:
- •Инвариантность ранга матрицы относительно элементарных преобразований.
- •Критерий существования обратной матрицы
- •Фундаментальной системой решений (фср), системы однородных линейных уравнений называется совокупность решений, которая обладает двумя свойствами:
- •Определение проекции вектора на ось:
- •Направляющие косинусы в декартовой системе координат
- •Линейная зависимость и независимость свободных векторов:
- •Критерий линейно зависимости свободных векторов
- •Определение базиса:
- •Теорема о базисе
- •Скалярное произведение векторов
- •Критерий линейной зависимости векторов линейного пространства
- •Параметрическое уравнение.
- •Уравнение плоскости проходящей через точку параллельно 2м коллинеарным векторам
- •Уравнение прямой проходящей через точку параллельно вектору
- •Каноническое уравнение прямой в пространстве
- •Взаимное расположение прямой и плоскости в пространстве
- •Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость .
- •Эллипс, свойства эллипса
- •Метод параллельных сечений исследования формы поверхности.
Инвариантность ранга матрицы относительно элементарных преобразований.
Элементарные преобразования матрицы:
-
Умножение строки на число отличное от нуля
-
Прибавление к одной строке другой строки
-
Перестановка строк
-
Те же преобразования столбцов
-
Детерминант матрицы не изменится, если к какой либо его строке (столбцу) прибавить линейную комбинацию остальных строк (столбцов)
Элементарные преобразования не меняют ранга матрицы
Доказательство:
При умножении строки на число λ≠0 базисный минор либо не изменится, либо умножится на λ. Ни один минор, равный нулю, не сделается отличным от нуля.
Если все миноры порядка r+1 равны нулю, то сложение строк не сделает ни один из них отличным от нуля.
При перестановке строк минор может изменить знак (если в него входят обе переставляемые строки), или может замениться на минор, не больше чем знаком отличающийся от другого минора той же матрицы (если содержит только одну из переставляемых строк), или вообще не изменится.
Неизменность ранга при элементарных преобразованиях столбцов доказывается аналогично.
Теорема о базисном миноре.
В матрице А размером mxn минор порядка r называется базисным, если он отличен от нуля, а все миноры порядка r+1 равны нулю или миноров порядка r+1 вообще нет, т.е. r совпадает с меньшими из чисел m или n.
ТЕОРЕМА
Кронекера – Капелли.
Система
линейных уравнений (5)
совместна тогда и только тогда, когда
ранг основной матрицы системы равен
рангу ее расширенной матрицы, т.е.
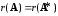 .
.
Критерий
единственности решения.
Система
линейных уравнений (5)
имеет единственное решение тогда и
только тогда, когда ранг основной матрицы
системы равен рангу ее расширенной
матрицы и равен числу переменных, т.е.
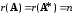 .
.
Элементарными преобразованиями СЛУ называются преобразования следующего вида:
1) умножение обеих
частей уравнения на число
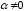 ;
;
2) прибавление к
одному уравнению другого, умноженного
на число
 ;
;
3) перестановка двух уравнений;
4) вычеркивание одного из двух пропорциональных или одинаковых уравнений.
Две СЛУ наз. эквивалентными если их решения совпадают
Метод Гаусса
Суть этого метода в том, что путем элементарных преобразований суммы из всех уравнений, кроме первого исключаем неизвестные х1. Далее из всех уравнений, кроме 1-го и 2-го исключаем неизвестные х2 т т.д.
На практике эти преобразования проводят над строками расширенной матрицы системы.
К элементарным преобразования относятся:
1. Умножение (деление) на число, отличное от нуля, элементов какой либо строки;
2. Сложение элементов какой либо строки с соответствующими элементами другой строки, предварительно умноженными на не нулевое число;
3. Перестановка строк матрицы;
4. Вычеркиванием из матрицы нулевых строк, одной из двух одинаковых строк, одной из двух пропорциональных строк, вычеркиваются строки, линейно – зависимые от других строк
В результате элементарно преобразованная расширенная матрица будет приведена к виду трапеции этот процесс называется прямым ходом метода Гаусса. Обратный ход метода Гаусса состоит в следующем: из последнего уравнения находим единственный входящий в него неизвестное, подставляем найденное значение неизвестного в предпоследнее уравнение неизвестного, находим еще одно значение неизвестного, пока не дойдем до 1-го уравнения, в котором уже найдены все неизвестные кроме одного
Обратной
к матрице
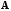 называется матрица, обозначаемая
называется матрица, обозначаемая
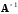 ,
такая, что
,
такая, что
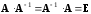 .
.
Квадратная матрица, определитель которой отличен от нуля, называется невырожденной
Свойства обратной матрицы
1.
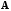 – квадратная.
– квадратная.
Действительно,
чтобы существовали произведения
 и
и
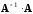 необходимо, чтобы матрицы
необходимо, чтобы матрицы
 и
и
 имели соответственно размеры
имели соответственно размеры
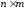 и
и
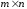 .
Тогда матрица
.
Тогда матрица
 будет иметь размер
будет иметь размер
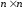 ,
а матрица
,
а матрица
 – размер
– размер
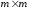 .
Но для равенства
.
Но для равенства
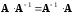 необходимо, чтобы размеры матриц
необходимо, чтобы размеры матриц
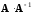 и
и
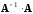 совпадали, т.е.
совпадали, т.е.
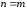 .
.
2. Если обратная матрица существует, то она единственная.
Действительно,
если предположить, что существует две
матрицы
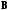 и
и
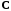 обладающие свойством
обладающие свойством
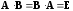 и
и
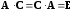 ,
,
то будет существовать
и произведение
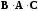 ,
причем
,
причем

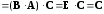
и 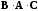
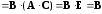 .
.
Следовательно, 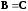 .
.
3.
Определитель матрицы
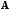 должен быть отличен от нуля.
должен быть отличен от нуля.
Действительно,
так как
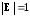 и для любых квадратных матриц
и для любых квадратных матриц
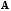 и
и
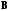
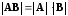 ,
то
,
то
 =>
=>
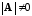 и
и
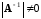 .
.
