
- •1. Определение матрицы. Виды матриц. Равенство матриц.
- •2. Линейные и нелинейные операции над матрицами
- •Умножение матриц. Свойства произведения матриц
- •3. Перестановка чисел, число инверсий, определитель
- •4.Минор к-порядка минор элемента матрицы, ранг
- •Метод окаймляющих миноров:
- •Инвариантность ранга матрицы относительно элементарных преобразований.
- •Критерий существования обратной матрицы
- •Фундаментальной системой решений (фср), системы однородных линейных уравнений называется совокупность решений, которая обладает двумя свойствами:
- •Определение проекции вектора на ось:
- •Направляющие косинусы в декартовой системе координат
- •Линейная зависимость и независимость свободных векторов:
- •Критерий линейно зависимости свободных векторов
- •Определение базиса:
- •Теорема о базисе
- •Скалярное произведение векторов
- •Критерий линейной зависимости векторов линейного пространства
- •Параметрическое уравнение.
- •Уравнение плоскости проходящей через точку параллельно 2м коллинеарным векторам
- •Уравнение прямой проходящей через точку параллельно вектору
- •Каноническое уравнение прямой в пространстве
- •Взаимное расположение прямой и плоскости в пространстве
- •Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость .
- •Эллипс, свойства эллипса
- •Метод параллельных сечений исследования формы поверхности.
Критерий линейной зависимости векторов линейного пространства
Векторы
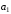 ,
,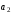 ,
, ,
,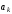 линейно зависимы тогда и только тогда,
когда хотя бы один из них линейно
выражается через оставшиеся.
линейно зависимы тогда и только тогда,
когда хотя бы один из них линейно
выражается через оставшиеся.
1) Необходимость.
Пусть векторы
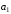 ,
,
 ,
,
 ,
,
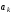 – линейно зависимы. Тогда по определению
существуют числа
– линейно зависимы. Тогда по определению
существуют числа
 ,
,
 ,
,
 ,
,
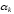 ,
не все равные нулю и такие, что
,
не все равные нулю и такие, что

 .
Пусть, например,
.
Пусть, например,
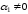 .
Тогда
.
Тогда
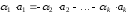 ,
⇒
,
⇒
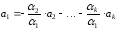 .
.
2) Достаточность.
Пусть один из векторов
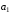 ,
,
 ,
,
 ,
,
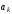 линейно выражается через оставшиеся.
Например, пусть
линейно выражается через оставшиеся.
Например, пусть
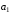
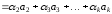 ,
⇒
,
⇒
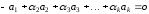 .
.
Следовательно,
векторы
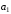 ,
,
 ,
,
 ,
,
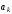 – линейно зависимы.
– линейно зависимы.
Понятия базиса и размерности линейного пространства
Максимальная линейно независимая система векторов линейного пространства называется базисом этого линейного пространства.
Если в линейном
пространстве
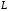 существует базис из
существует базис из
 векторов, то пространство называют
конечномерным, а
векторов, то пространство называют
конечномерным, а
 называют размерностью линейного
пространства (пишут:
называют размерностью линейного
пространства (пишут:
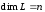 ).
).
Если в линейном
пространстве
 для любого натурального
для любого натурального
 можно найти линейно независимую систему
векторов, то пространство называют
бесконечномерным (пишут:
можно найти линейно независимую систему
векторов, то пространство называют
бесконечномерным (пишут:
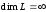 ).
).
ТЕОРЕМА. (Связь между координатами вектора в разных базисах).
Пусть
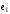 ,
,
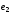 ,
,
 ,
,
 и
и
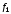 ,
,
 ,
,
 ,
,
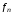 – два базиса линейного пространства
– два базиса линейного пространства
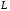 .
Причем имеют место равенства:
.
Причем имеют место равенства:

Если вектор
 имеет в базисе
имеет в базисе
 ,
,
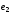 ,
,
 ,
,
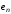 координаты
координаты
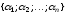 ,
в базисе
,
в базисе
 ,
,
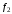 ,
,
 ,
,
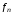 – координаты
– координаты
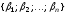 ,
то справедливо равенство
,
то справедливо равенство
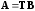 ,
,
где
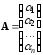 ,
,
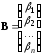 ,
,
 .
.
Матрицу
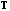 называют матрицей перехода от базиса
называют матрицей перехода от базиса
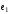 ,
,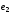 ,
, ,
,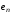 к базису
к базису
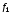 ,
, ,
, ,
,
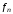 .
.
ДОКАЗАТЕЛЬСТВО
По условию 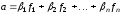 .
.
Расписывая
векторы
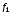 ,
, ,
, ,
,
 по базису
по базису
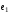 ,
,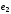 ,
, ,
, ,
получим:
,
получим:
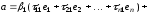

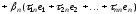 .
.
Раскроем скобки и перегруппируем слагаемые:
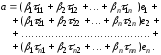 (1)
(1)
Так
как по условию
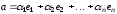 ,
то из (1) получаем:
,
то из (1) получаем:
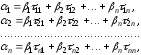
или
в матричном виде 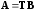 .
.
Понятие линейного оператора
Пусть
 и
и
 – линейные пространства над
– линейные пространства над
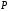 (где
(где
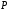 = ℝ
или
= ℝ
или
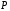 = ℂ
= ℂ ).Пусть
каждому вектору
).Пусть
каждому вектору
 ставится в соответствие однозначно
определенный вектор
ставится в соответствие однозначно
определенный вектор
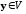 ,
т.е. задана функция
,
т.е. задана функция
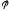 с областью определения
с областью определения
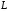 и областью значения
и областью значения
 .
Такую функцию принято называть оператором
(преобразованием),
действующим
из
.
Такую функцию принято называть оператором
(преобразованием),
действующим
из
 в
в
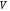 .
Вектор
.
Вектор
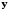 называется образом
вектора
называется образом
вектора
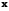 и обозначают
и обозначают
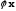 ,
а
,
а
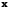 называется прообразом
вектора
называется прообразом
вектора
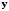 .
Оператор, действующий из
.
Оператор, действующий из
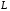 в
в
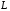 ,
называют оператором
пространства
,
называют оператором
пространства
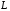 .
.
Оператор
 называется линейным,
если для любых
называется линейным,
если для любых
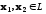 и любого
и любого
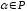 выполнены следующие условия:
выполнены следующие условия:
1)
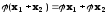 ,
2)
,
2)
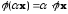
Матрица линейного оператора
Так
как
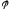 – оператор пространства
– оператор пространства
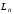 ,
т.е. векторы
,
т.е. векторы

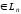 ,
то их можно разложить по базису
,
то их можно разложить по базису
 :
:
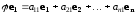


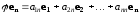
Составим матрицу
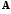 из коэффициентов разложения векторов
из коэффициентов разложения векторов
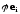 по базису
по базису
 :
:
 .
.
Эту
матрицу называют матрицей
линейного оператора
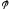 в базисе
в базисе
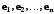 (относительно базиса
(относительно базиса
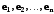 ).
).
Уравнение прямой на плоскости
 – произвольная
точка.
– произвольная
точка.
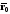 и
и
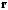 – радиус-векторы точек
– радиус-векторы точек
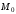 и
и
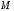 .
Рассмотрим векторы
.
Рассмотрим векторы
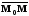
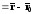 и
и
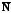 .
.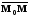
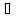
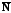 =>
=>
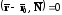 , (23)
, (23)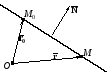
или,
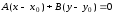 .
.
Этому уравнению
удовлетворяют координаты любой точки
прямой и не удовлетворяют координаты
других точек плоскости. Данное
уравнение называют уравнениями
прямой, проходящей через точку
 Выполним
преобразования
Выполним
преобразования
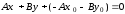 .
.
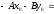
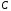 получим общее
уравнение прямой на плоскости:
получим общее
уравнение прямой на плоскости: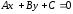
Вектор
 перпендикулярен данной прямой.
перпендикулярен данной прямой.
Параметрическое уравнение.
Дана
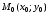 и
и
 .
Составим уравнение прямой, проходящей
через М0
параллельно вектору l.
.
Составим уравнение прямой, проходящей
через М0
параллельно вектору l.
Вектор, параллельный
прямой, называют направляющим
вектором
этой прямой.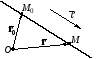
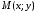 – текущая точка
прямой,
– текущая точка
прямой,
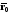 и
и
 – радиус-векторы точек
– радиус-векторы точек
 и
и
 .
Рассмотрим
.
Рассмотрим
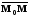
 и
и
 .
По условию задачи они параллельны.
Следовательно, существует такое число
.
По условию задачи они параллельны.
Следовательно, существует такое число
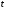 ,
что
,
что 
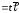 ,⇒
,⇒
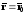
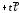 , (27)
, (27)
или 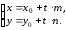
Данной системе
удовлетворяют координаты любой точки
прямой при некотором значении
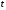 и не будут удовлетворять координаты
других точек плоскости.
и не будут удовлетворять координаты
других точек плоскости.
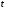 - параметр.
- параметр.
Полученную систему уравнений называют параметрическим уравнением прямой.
Каноническое уравнение прямой
Из параметрического уравнения прямой
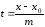 и
и
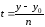 ,
,

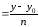 ,
,
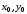 – координаты
некоторой точки на прямой,
– координаты
некоторой точки на прямой,
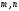 – координаты направляющего вектора
прямой.
– координаты направляющего вектора
прямой.
Данное уравнение называют каноническим уравнением прямой на плоскости.
Уравнение прямой, проходящей через две точки
Даны две точки
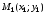 и
и
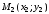 .
Тогда
.
Тогда
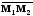
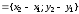 является ее направляющим и каноническое
уравнение этой прямой будет иметь
вид
является ее направляющим и каноническое
уравнение этой прямой будет иметь
вид .Данное
уравнение наз. уравнением прямой проход.
ч/з 2 точки. из канонич. получ. параметрич.
.Данное
уравнение наз. уравнением прямой проход.
ч/з 2 точки. из канонич. получ. параметрич.
Взаимное расположение прямых на плоскости.
М
Если на плоскости даны две прямые, то
они либо параллельны, либо пересекаются.
Если прямые параллельны, то их нормальные
векторы
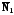 и
и
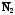 коллинеарные, а углы наклона к оси
коллинеарные, а углы наклона к оси
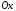 (
(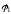 и
и
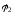 )
– равные.
)
– равные.
Пусть
прямые
 и
и
 заданы общими уравнениями
заданы общими уравнениями
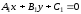 и
и
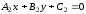 .
Тогда
.
Тогда
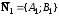 и
и
 .
Так как коллинеарные векторы имеют
пропорциональные координаты, то прямые
.
Так как коллинеарные векторы имеют
пропорциональные координаты, то прямые
 и
и
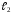 параллельны тогда и только тогда, когда
в их общих уравнениях коэффициенты при
соответствующих неизвестных
пропорциональны, т.е.
параллельны тогда и только тогда, когда
в их общих уравнениях коэффициенты при
соответствующих неизвестных
пропорциональны, т.е.
 .
.
Пусть прямые
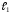 и
и
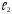 заданы уравнениями с угловым коэффициентом
заданы уравнениями с угловым коэффициентом
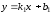 и
и
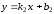 соответственно. Так как
соответственно. Так как
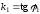 и
и
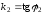 ,
то прямые
,
то прямые
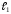 и
и
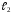 параллельны тогда и только тогда, когда
их угловые коэффициенты пропорциональны,
т.е.
параллельны тогда и только тогда, когда
их угловые коэффициенты пропорциональны,
т.е.
 .
.
При пересечение
прямых на плоскости образуется две пары
вертикальных углов. 
Один из углов (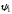 ),
образуемых прямыми
),
образуемых прямыми
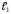 и
и
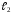 ,
равен углу между их нормальными векторами
,
равен углу между их нормальными векторами
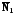 и
и
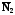 .
Следовательно, если прямые
.
Следовательно, если прямые
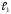 и
и
 заданы общими уравнениями
заданы общими уравнениями
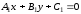 и
и
 соответственно, то
соответственно, то
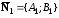 ,
,
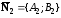 и
и

Второй угол
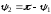 и, следовательно,
и, следовательно,
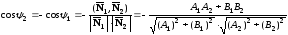 .
.
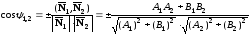 ,
,
или 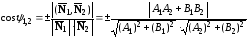 ,
,
+ если угол острый, - если угол тупой.
Если
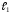 и
и
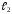 перпендикулярны, то
перпендикулярны, то
 и
и
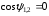 .
Из формулы получаем
.
Из формулы получаем
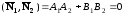 –
критерий перпендикулярности прямых,
заданных общими уравнениями.
–
критерий перпендикулярности прямых,
заданных общими уравнениями.
Прямые с угловым коэффициентом
прямые
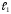 и
и
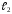 заданы уравнениями с угловым коэффициентом
заданы уравнениями с угловым коэффициентом
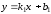 и
и
 .
Острый угол между прямыми будет равен
.
Острый угол между прямыми будет равен
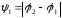 .
.
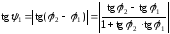 ,⇒
,⇒
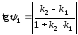 .
.
Так как тупой угол
между прямыми
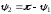 ,
то
,
то
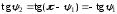
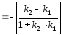 .
.
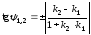 ,
,
+ для острого угла, - для тупого.
если
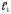

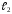 , то
, то
 и
и
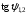 не существует. Но это означает, что
знаменатель дроби в обращается в ноль,
т.е.
не существует. Но это означает, что
знаменатель дроби в обращается в ноль,
т.е.
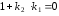 ,⇒
,⇒
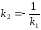 –
критерий
перпендикулярности прямых, имеющий
угловые коэффициенты
–
критерий
перпендикулярности прямых, имеющий
угловые коэффициенты
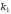 и
и
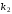 .
.
Уравнение плоскости
Составим уравнение
плоскости, проходящей через точку
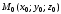 ,
перпендикулярно вектору
,
перпендикулярно вектору
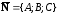 .
.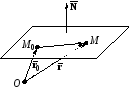
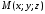 – текущая точка
плоскости,
– текущая точка
плоскости,
 и
и
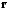 –
радиус-векторы точек
–
радиус-векторы точек
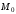 и
и
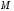 соответственно.
соответственно.
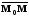
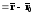
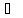
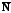 .
=>
.
=>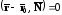 ,или,
,или,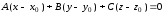 . (37)
. (37)
Данное уравнение
называют уравнением
плоскости, проходящей через точку
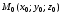 перпендикулярно вектору
перпендикулярно вектору
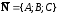 .
.
преобразуем данное
уравнение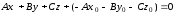 .
.
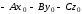 =
=
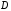 и получим общее уравнение плоскости
и получим общее уравнение плоскости

Если в уравнении
все коэффициенты
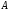 ,
,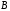 ,
, и
и
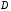 отличны от нуля, то уравнение называют
полным;
если хотя бы один из коэффициентов равен
нулю – уравнение называют неполным.
отличны от нуля, то уравнение называют
полным;
если хотя бы один из коэффициентов равен
нулю – уравнение называют неполным.
