
- •Тема: Введение. Основные уравнения электромагнитного поля
- •1.2. Уравнения максвелла в интегро-дифференциальной формах и их физический смысл
- •1.3. Метод векторных комплексных амплитуд. Уравнения максвелла в комплексной форме
- •1.3.3.Комплексная диэлектрическая проницаемость среды
- •Лекция № 2
- •1. Закон сохранения энергии электромагнитного поля
- •2.2. Волновые уравнения и волновой характер электромагнитного поля
- •Лекция № 3 решения уравнений максвелла
- •1.Методы решения уравнений Максвелла
- •2. Метод электродинамических потенциалов
- •Лекция № 4 Тема № 4. Излучение электромагнитных волн элементарными излучателями
- •1.Совершенствовать фундаментальные знания по специальности;
- •2.Формировать интерес и активность в изучении дисциплины.
- •4.1.Понятие об элементарных излучателях. Элементарный электрический излучатель и его модель
- •Уравнения электростатики:
- •Электромагнитная волна, сформированная элементарным электрическим излучателем, будет иметь вид известных нам уравнений гельмгольца
- •4.2. Методика нахождения векторов поля ээи
- •4.2.4. Электромагнитное поле в ближней и дальней зонах элементарного электрического излучателя
- •4.2.4.1.Поле элементарного электрического излучателя в ближней зоне
- •4.2.4.2. Поле элементарного электрического излучателя в дальней зоне
- •4.2.5.Параметры элементарного электрического излучателя
- •4.3. Элементарный магнитный излучатель и его модель
- •4.3.1.Поле излучения элементарной рамки
- •2.8. Поле излучения элементарного щелевого вибратора
- •Глава 3 Электромагнитные волны в однородных изотропных средах
- •3.1. Плоская волна, как частный случай сферической (цилиндрической) волны. Структура поля и основные параметры
- •3.2.Особенности распространения плоских волн в однородных изотропных средах
- •3.2.4. Распространение плоской волны в хорошо проводящей среде
- •3.3. Поляризация электромагнитных волн. Создание эмв различной поляризации реальными излучателями
- •Глава 4 Электромагнитные волны в анизотропных средах
- •4.1.Понятие об анизотропных средах. Уравнения максвелла для анизотропных сред
- •4.3. Распространение электромагнитных волн в поперечно -намагниченном феррите ( плазме)
- •Глава 1. Основные законы и методы электродинамики_______________ 9
- •Глава 2. Излучение электромагнитных волн элементарными из-
- •Глава 3. Электромагнитные волны в однородных изотропных
- •Глава 4. Электромагнитные волны в анизотропных средах____________ 87
Электромагнитная волна, сформированная элементарным электрическим излучателем, будет иметь вид известных нам уравнений гельмгольца
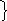 ▼2
Н
+ к 2 Н
= 0;
▼2
Н
+ к 2 Н
= 0;
▼2 Е + к 2 Е = 0. (4.8)
 При
наличии источника поля в виде зарядов
ρ и тока δ
уравнения Гельмгольца примут вид
При
наличии источника поля в виде зарядов
ρ и тока δ
уравнения Гельмгольца примут вид
▼2 Н + к 2 Н = - rot δ;
▼2 Е + к 2 Е = jωμδ + (1/ ε) grad ρ. (4.9)
Полученные неоднородные волновые уравнения (4.9) отличаются от уравнений (4.8) наличием в правой части плотности сторонних зарядов и токов. Искать решение уравнений (4.9), как задачи об излучении, в виде нахождения векторов поля в заданной точке M(xyz) достаточно сложная задача. Для упрощения решения вводят вспомогательные функции. Такими функциями, например, могут быть электродинамические потенциалы.
4.2. Методика нахождения векторов поля ээи
4.2.1. Модели элементарных электрических излучателей
Для практического использования в качестве модели элементарного излучателя предлагается рассмотреть две схемы. Первая состоит из генератора, подключенного с помощью проводников к разнесенным обкладкам конденсатора. Обкладки представляют собой плоские металлические поверхности, между которыми образуется переменное электрическое поле (рис. 4.5). Вторая схема отличается от первой тем, что пластины заменены металлическими шарами. Эта модель была впервые использована Генрихом Герцем и получила название ДИПОЛЬ ГЕРЦА (рис.4.6).


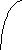
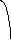







 U
~ Е
U
~ Е


Рис.4.5
 Эпюра
тока Условие элементарности
Эпюра
тока Условие элементарности




 l
<< λ
l
<< λ
δ d << l



 U
~ l
U
~ l


Рис. 4.6
4.2.2.Вывод выражений для поля элементарного электрического излучателя
Пусть элементарный электрический излучатель расположен вдоль оси z, плотность гармонически изменяющегося тока δ = δм sin ωt. Задачей является нахождение векторов поля в произвольной точке М(xyz). Учитывая, что излучатель практически точечный и расположен в свободном пространстве, образуемый им фронт волны будет сферической формы. Воспользовавшись сферической системой координат, составим искомые векторы, которыми будут Еφ, Еθ, Еr, Нφ, Нθ, Нr. На рисунке 4.7 представлена сферическая система координат [1-6]. Из рисунка видно, что в точке М будут векторы поля, то есть Е r ≠ 0, Е θ ≠ 0 и Н φ ≠ 0, так как векторы Еφ = Н θ = Н r = 0. Действительно, магнитное поле симметрично, поэтому существует только Нφ.
Z r
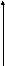


 Е
r
Е
r
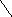


 Н φ
Н φ
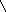


 Θ
Θ



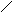 М(xyz)
М(xyz)
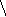

 δ
Е θ y
δ
Е θ y





 φ
φ
x Рис.4.7
Электрический вектор Еθ создается вектором Н φ, а вектор Е r - движущимися зарядами. Исходя из малых размеров длины l и поперечного сечения S электрический момент излучателя определится
+ l / 2
Рэ = ∫ δ dv = ∫ δ ∫ dz = I l . (4.10)
V S ─l / 2
Ток I протекает вдоль оси диполя или вдоль координаты z, и для выбранной сферической системы равен [1]
I z0 = I ( r0cosθ - θ 0 sinθ), (4.11)
где z0 , r0, θ0 – орты соответствующих координат.
Тогда векторный потенциал А
μ I l е ─j кr
А = ―― ―― ( r0cosθ + θ0sinθ). (4.12)
4 π r
По векторному потенциалу определяется вектор магнитного поля Н φ из выражения связи (3.10)
Н φ = (1/μ) rot А φ. (4.13)
В сферической системе координат


r 0 rθ0 r sinθ φ0
1 ∂ ∂ ∂
rot А = ――― ―― ―― ―― (4.14)
r 2 sinθ ∂ r ∂ θ ∂ φ
А r r А θ r sinθ А φ
Из выражения (4.12) следует, что
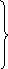 μ I l е j к r
μ I l е j к r
А r = ――― ―― cos θ;
4 π r (4.15)
μ I l е ─j к r
А θ = ─ ――― ―― sinθ; А φ = 0.
4 π r
Из выражений системы (4.15) следует, что ни одна из составляющих векторного потенциала не зависит от угловой координаты φ. Это значит, что поле элементарного электрического излучателя обладает осевой симметрией и потому ∂ ⁄ ∂φ = 0. Для нахождения вектора Н φ необходимо подставить значения векторных потенциалов А r , А θ , Аφ из выражений (4.15) в оператор (4.14) и полученное значение rotА подставить в выражение связи (4.13). После преобразований определится выражение вектора магнитного поля Нφ в искомой точке М
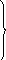 I
l
к2
1 j
I
l
к2
1 j
Н φ = ―― [ ―― + ――] sinθ е─j к r ; (4.16)
4 π (к r) 2 (к r)
Н r = Н θ = 0.
Вектор напряженности электрического поля можно найти, воспользовавшись первым уравнением Максвелла. Так как вне вибратора нет токов проводимости δ = 0, то rot Н = j ω ε Е, откуда Е = -- j rot Н / ω ε . (4.17)
После использования выражений (4.16), (4.17) и их преобразования получаются выражения для векторов электрического поля в виде
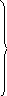 I
l
к3
j
1
I
l
к3
j
1
Е r = ─ ――― [ ―― ─ ―― ] cos θ е –j к r ;
2 π ω ε (кr) 3 (кr) 2
I l к 3 j 1 j (4.18)
Е θ = ─ ――― [ ―― ─ ―― ─ ――] sinθ е –j к r ;
4 π ω ε (кr) 3 (кr) 2 (кr)
Е φ = 0.
Формулы (4.16) описывают магнитную, а формулы (4.18) - электрическую составляющие поля излучения элементарного электрического диполя в точке М. Из указанных формул и рисунка 4.7 видно:
- вектор электрического поля Е всегда лежит в плоскости, проходящей через ось диполя и точку М(xyz);
- плоскость, в которой лежит вектор Е, называется меридиальной или плоскостью Е;
- вектор напряженности магнитного поля Н всегда перпендикулярен меридиальной плоскости, то есть имеет широтную ориентацию;
- плоскость, в которой располагается магнитный вектор, есть плоскость, перпендикулярная оси диполя и проходящая через его середину называется экваториальной или плоскостью Н;
- оба вектора Е и Н зависят от координат r и θ сферической системы и не зависят от координаты φ;
- поле неравномерно распределено в пространстве, так как значения sinθ и cosθ как сомножители в формулах меняются от 0 до 1, и обладает осевой симметрией;
- векторы Е и Н взаимно перпендикулярны;
- значения векторов изменяются с изменением расстояния по закону 1/ r, причем расстояние r измеряется в волновых числах, то есть как кr;
- множитель е – j к r определяет положение вектора в точке М;
- ∫( е – j к r/ r)dr – интеграл Зоммерфельда, решается он использованием теории рядов, поэтому в формулах этот интеграл представлен весомыми члены сходящегося ряда.
Таким образом, поле элементарного электрического излучателя имеет характер сферической волны, содержит взаимно связанные векторы Е и Н.
