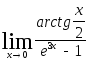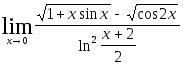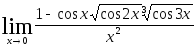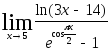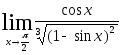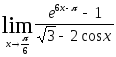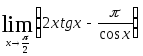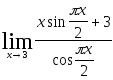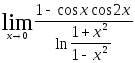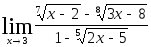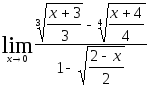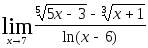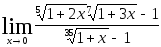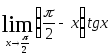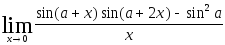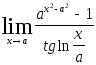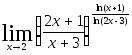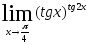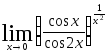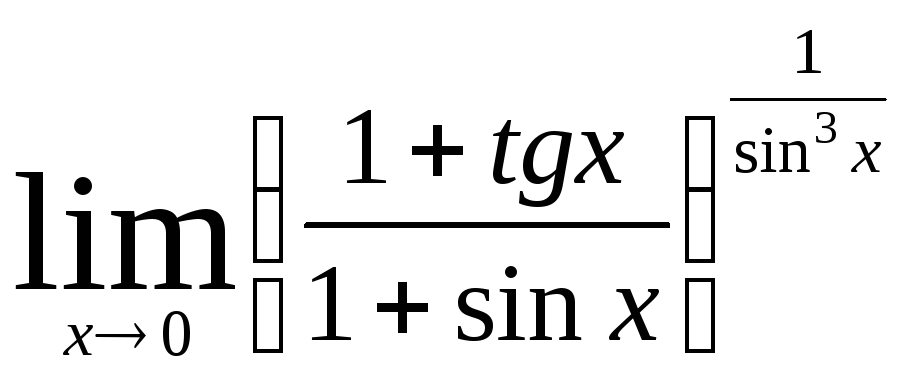- •Содержание
- •Предисловие
- •Глава 1. Элементы аналитической геометрии и линейной алгебры
- •§1. Семинарские занятия Семинар №1
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •Семинар №2 Точка и прямая на плоскости. Окружность.
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •Семинар № 3 Кривые второго порядка.
- •Задачи для решения на семинаре
- •Семинар № 4 Векторная алгебра.
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •Семинар № 5 Прямая и плоскость в пространстве
- •Задачи для решения на семинаре
- •Семинар № 6 Матрицы. Действия над матрицами.
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •Семинар № 7 Ранг матрицы. Системы линейных уравнений.
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •§ 2. Примерное содержание рейтинговых контрольных работ в первом семестре
- •§ 3. Методы построения графиков функций Графики некоторых функций
- •Некоторые функции, примыкающие к элементарным
- •Глава 2. Предел функции. Непрерывность
- •§ 2.1. Предел числовой последовательности
- •1.1. Определение числовой последовательности
- •1.2. Предел числовой последовательности
- •1.3. Свойства передела
- •Упражнения к § 2.1
- •§ 2.2. Предел функции. Методы вычисления предела
- •1. Определение предела функции
- •2. Свойства предела функции
- •3. Методы вычисления предела функции
- •5. Неопределенность .
- •Упражнения к § 2.2
- •§ 2.3. Эквивалентные бесконечно малые. Применение эквивалентности при вычислении пределов
- •§2.4. Непрерывность. Точки разрыва. График функции
- •2. Понятие о точках разрыва и их классификация
- •2) Точки разрыва 1-го рода (конечный разрыв)
- •3) Точки разрыва 2-го рода (бесконечный разрыв)
- •3. Об асимптотах графика функции
- •§ 2.5. Производная. Дифференцирование функций
- •1. Производные функций, заданных явно
- •Упражнения к § 2.5
- •2. Производные высших порядков явных функций
- •3. Производные функций, заданных параметрически
- •4. Производные функций, заданных неявно
- •§ 2.6. Вычисление пределов с помощью правила Лопиталя
- •1. Неопределенности и .
- •2. Другие неопределенности
- •Упражнения к § 2.6
- •§ 2.7. Применение формулы Тейлора при вычислении предела функции
- •Упражнения к § 2.7
- •Ответы к главе 2
- •Литература
§ 2.3. Эквивалентные бесконечно малые. Применение эквивалентности при вычислении пределов
Определение
1. Функция
![]() называется бесконечно малой при
называется бесконечно малой при
![]() (или
(или
![]() ),
если
),
если
 (или
(или
![]() ).
).
Определение 2. Две бесконечно малые называются эквивалентными, если предел их отношения равен 1.
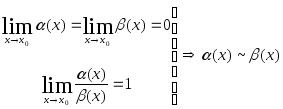
Теорема.
Предел отношения двух бесконечно малых
(неопределенность
![]() )
равен пределу отношения двух других
бесконечно малых, эквивалентных данным,
т.е.
)
равен пределу отношения двух других
бесконечно малых, эквивалентных данным,
т.е.
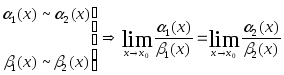 .
.
Отметим
также: если
![]() ,
то
,
то
![]() .
.
Основные формулы эквивалентности бесконечно малых.
Первый
замечательный предел ![]()
Первая группа формул эквивалентности
![]()
![]()
![]()
Вторя группа формул эквивалентности
![]()

![]()
Третья группа формул эквивалентности

![]() ,
,
![]()
![]() ,
,
![]()
![]()
Четвертая группа формул эквивалентности
![]()
 ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]()
Все эти четыре группы формул составляют таблицу эквивалентных бесконечно малых.
Сравнение бесконечно малых
Пусть
при
![]() функции
функции
![]() и
и
![]() являются бесконечно малыми. Две бесконечно
малые называются сравнимыми, если
существует предел их отношения
являются бесконечно малыми. Две бесконечно
малые называются сравнимыми, если
существует предел их отношения
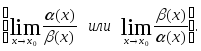
При этом могут быть следующие случаи:
1.
Если
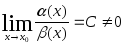 ,
то
,
то
![]() и
и
![]() бесконечно малые одного порядка.
бесконечно малые одного порядка.
2.
Если
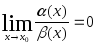 ,
то
,
то
![]() бесконечно малая более высокого порядка,
чем
бесконечно малая более высокого порядка,
чем
![]() .
Это записывается так:
.
Это записывается так:
![]() .
Читается так:
.
Читается так:
![]() равно о
равно о![]() малое
от
малое
от
![]() .
.
При
этом, если
![]() такое, что
такое, что
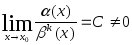 ,
то говорят, что
,
то говорят, что
![]() есть бесконечно малая порядка “k”
относительно
есть бесконечно малая порядка “k”
относительно
![]() .
.
3.
Если
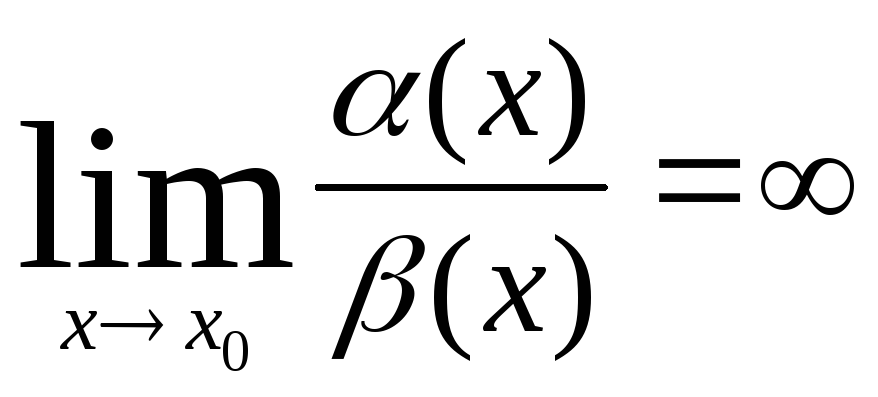 ,
то
,
то
![]() .
.
4.
Как уже было сказано выше, если
 ,
то бесконечно малые называются
эквивалентными :
,
то бесконечно малые называются
эквивалентными :
![]() .
.
5.
Если
![]() не существует, то
не существует, то
![]() и
и
![]() не сравнимые.
не сравнимые.
Упражнения к § 2.3
Найти пределы, используя эквивалентность бесконечно малых.
|
2.111.
|
2.112.
|
|
||
|
2.113.
|
2.114.
|
|
||
|
2.115.
|
2.116.
|
|
||
|
2.117.
|
2.118.
|
|
||
|
2.119.
|
2.120.
|
|
||
|
2.121.
|
2.122.
|
|
||
|
2.123.
|
2.124.
|
|
||
|
2.125.
|
2.126.
|
|
||
|
2.127.
|
2.128.
|
|
||
|
2.129.
|
2.130.
|
|
||
|
2.131.
|
2.132.
|
|
||
|
2.133.
|
2.134.
|
|
||
|
2.135.
|
2.136.
|
|
||
|
2.137.
|
2.138.
|
|
||
|
2.139.
|
2.140.
|
|
||
|
2.141.
|
||||
|
2.142.
|
||||
|
2.143.
|
2.144.
|
|
||
|
2.145.
|
2.146.
|
|
||
|
2.147.
|
||||
|
2.148.
|
2.149.
|
|
||
|
2.150.
|
2.151.
|
|
||
|
2.152.
|
2.153.
|
|
||
|
2.154.
|
2.155.
|
|
||
|
2.156.
|
2.157.
|
|
||
|
2.158.
|
2159.
|
|
||
|
2.160.
|
2.161.
|
|
||
|
2.162.
|
2.163.
|
|
||
|
2.164.
|
2.165.
|
|
||
|
2.166.
|
2.167.
|
|
||
|
2.168.
|
2.169.
|
|
||
|
2.170.
|
2.171.
|
|
||
|
2.172.
|
2.173.
|
|
||
|
2.174.
|
|
|||
2.175.
При
![]() функции
функции
![]() и
и
![]() бесконечно малые. Сравните их.
бесконечно малые. Сравните их.
2.175
(а).
При
![]() сравнить бесконечно малые
сравнить бесконечно малые
![]() и
и
![]() .
.
2.176.
Доказать, что при
![]()
![]() и
и
![]() эквивалентные бесконечно малые.
эквивалентные бесконечно малые.
2.177.
Дана функция y=x3.
Доказать, что при
![]() приращения
приращения
![]() и
и
![]() бесконечно малые одного порядка. При
каком значении x
бесконечно малые одного порядка. При
каком значении x
![]() и
и
![]() эквивалентные?
эквивалентные?
2.178.
Определить порядок малости относительно
x
следующих функций
![]() :
:
|
а)
|
б)
|
в)
|
|
г)
|
д)
|
е)
|
2.179.
Пользуясь таблицей эквивалентных
бесконечно малых, вывести формулы для
приближенных вычислений
![]() с точностью до членов второго порядка
(x2)
с точностью до членов второго порядка
(x2)
|
а)
|
б)
|
|
в)
|
г)
|
С помощью полученных формул приближенно вычислить:
|
1)
|
2)
|
3)
|
4)
|
|
|
5)
![]() ,
6)
,
6)
![]() .
.
2.180.
Доказать эквивалентность функций (при
![]() ):
):
![]() и
и
![]() .
.