2.5 Граничные условия для векторов поля
Под граничными условиями в теории поля понимают правила поведения векторов поля при переходе из одной среды – в другую (на границе раздела сред). Граница раздела S и характеристики сред показаны на рисунке 2.2.
Рисунок 2.2 – Векторы поля на границе раздела сред
Поскольку любой вектор может быть разделен на нормальную и тангенциальную (касательную) составляющие:
то граничные условия удобно сформулировать раздельно для нормальных и тангенциальных составляющих векторов ЭМП. Эти условия сводятся к следующим положениям.
1 Нормальные составляющие векторов магнитной индукции на границе раздела сред непрерывны:
.
(2.20)
2 Если поверхностный заряд на границе раздела сред отсутствует, то нормальные составляющие векторов электрического смещения непрерывны:
.
(2.21)
3 Если на границе раздела равномерно
распределен поверхностный заряд с
удельной плотностью
,
то справедливо соотношение:
.
(2.22)
4 Касательные составляющие векторов напряженности электрического поля на границе раздела сред непрерывны:
.
5 Касательные составляющие векторов напряженности магнитного поля на границе раздела сред непрерывны:
.
6 На поверхности хорошо проводящей среды
(
)
тангенциальная составляющая магнитного
поля наводит поверхностный электрический
ток с плотностью
.
Между полем и током выполняется
соотношение:
(2.23)
Таким образом, магнитное поле наводит
на поверхности проводника электрический
ток, который перпендикулярен вектору
магнитного поля
.
Контрольные вопросы:
1 Определение вектора напряженности электрического поля.
2 Определение вектора напряженности магнитного поля.
3 Связь векторов поля и векторов индукции.
4 Система уравнений Максвелла в дифференциальной форме.
5 Система уравнений Максвелла в интегральной форме.
6 Физическая трактовка источников электромагнитного поля.
7 Характеристики материальных сред.
8 Определение компонентов поля для гармонических колебаний.
9 Представление диэлектрической проницаемости на комплексной плоскости.
10 Формулировка закона сохранения энергии для электромагнитного поля.
11 Поведение векторов поля
и
вблизи проводящей поверхности.
3 Плоские электромагнитные волны
3.1 Характеристики плоской скалярной волны
Волнами называются колебательные движения непрерывных сред. Электромагнитные волны (ЭМВ) попадают под это определение. Для уяснения основных моментов колебаний рассмотрим простейший случай – однородную плоскую скалярную волну. Математически такая волна описывается формулой:
.
(3.1)
Процесс изменяется в пространстве (z) и во времени (t), Vm – амплитуда волны, ω – круговая частота, β – коэффициент фазы.
Временная и пространственная зависимость
описывается гармонической функцией. В
точке z = 0:
.
В точке z > 0:
,
т.е. колебания запаздывают на величину
βz. Уточним временную
зависимость колебаний. В начальный
момент времени (t
= 0)
.
Коэффициент фазы β
играет здесь роль пространственной
частоты. Размерность β
– рад/м, 1/м. Временной период волны
.
На рисунке 3.1 показано пространственное изменение поля для двух моментов времени.
Рисунок 3.1 – Плоская скалярная волна
Пространственный период λ
– длина волны
.
Рассматриваемая волна называется плоской, это значит, что в любой плоскости, перпендикулярной оси 0z, волна имеет одинаковую фазу. Эта плоскость называется фронтом волны. Уравнение фронта волны:
.
Скорость перемещения фронта волны называется фазовой скоростью:
.
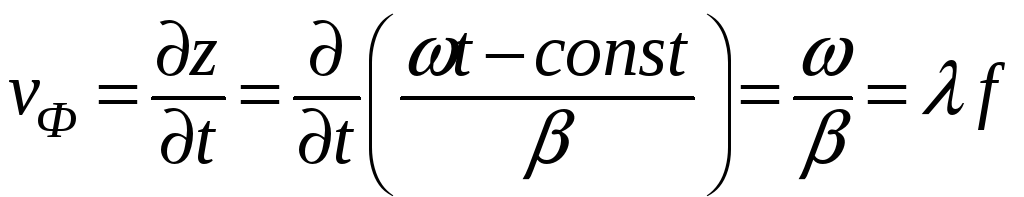(3.2)
Волна, распространяющаяся в направлении убывания координаты z, записывается аналогично (3.1):
,
(3.3)
и имеет такую же скорость распространения, как и прямая.
Реальные среды обладают потерями, что приводит к затуханию волны в процессе распространения. Закон изменения амплитуды волны можно записать так:
,
где α – коэффициент затухания (ослабления) плоской волны с размерностью 1/м.
В расчетах также пользуются логарифмической единицей – погонным затуханием:
.
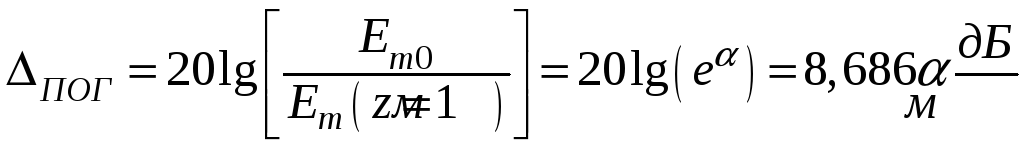(3.4)
Пространственная структура волны представлена на рисунке 3.2.
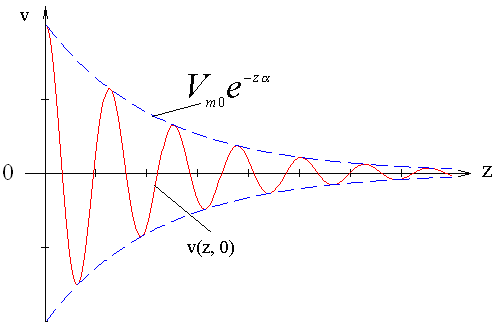
Рисунок 3.2 – Затухающая волна в среде с потерями
Коэффициент фазы β и коэффициент затухания α являются показателями экспоненты и могут быть объединены в единую комплексную величину, которая называется коэффициентом распространения:
.
(3.5)
В среде без потерь коэффициент
распространения величина чисто мнимая
.