
- •Содержание
- •Часть 2 линии передач и их элементы 40
- •Часть 3 многополюсники сверхвысоких частот 88
- •Предисловие
- •Часть 1 основы теории электромагнитного поля
- •1 Скалярные и векторные поля. Операции над векторами
- •1.1 Классификация полей
- •1.2 Операции над векторами
- •2 Основные положения теории электромагнитного поля
- •2.1 Определение векторов электромагнитного поля
- •2.2 Уравнения Максвелла
- •2.3 Уравнения Максвелла для гармонических колебаний. Комплексные амплитуды
- •2.4 Энергия электромагнитного поля
- •2.5 Граничные условия для векторов поля
- •3 Плоские электромагнитные волны
- •3.1 Характеристики плоской скалярной волны
- •3.2 Плоская электромагнитная волна
- •3.3 Частные случаи распространения плоских электромагнитных волн
- •3.4 Падение плоской электромагнитной волны на границу раздела сред
- •4 Излучение электромагнитных волн
- •4.1 Элементарные источники излучения
- •4.2 Основные электрические характеристики антенн
- •4.3 Типы антенн
- •Часть 2 линии передач и их элементы
- •5 Линии передач. Резонаторы
- •5.1 Определения
- •5.2 Электрические характеристики регулярных линий
- •5.3 Коаксиальная линия
- •5.4 Двухпроводная линия
- •5.5 Прямоугольный волновод. Волна основного типа
- •5.6 Круглые волноводы
- •5.7 Полосковые линии
- •5.8 Световоды
- •5.9 Объемные резонаторы
- •Контрольные вопросы:
- •6 Расчет режимов работы нагруженных линий
- •6.1 Волновые процессы в нагруженных линиях
- •6.2 Режимы работы нагруженных линий
- •6.3 Круговая диаграмма
- •Контрольные вопросы:
- •7 Согласование нагрузок с линиями передач
- •7.1 Цели и критерии согласования
- •7.2 Согласование нагрузок методом четвертьволнового трансформатора
- •7.3 Согласование методом параллельного шлейфа
- •Контрольные вопросы:
- •8 Элементы линий передач
- •8.1 Классификация элементов
- •8.2 Элементы коаксиальных трактов
- •8.3 Элементы трактов, выполненных на прямоугольных волноводах
- •8.4 Трансформаторы типов волн
- •Контрольные вопросы:
- •Часть 3 многополюсники сверхвысоких частот
- •9 Матричное описание многополюсников сверхвысоких частот
- •9.1 Определение многополюсников
- •9.2 Матрицы 4-полюсника и их свойства
- •9.3 Матрицы многополюсников
- •10 Частотно-избирательные фильтры свч
- •10.1 Основные определения
- •10.2 Структура фильтров. Способы расчета
- •8 Пример реализации фильтра со ступенчатой структурой.
- •11 Балансные многополюсники
- •11.1 Общие свойства
- •11.2 Некоторые типы балансных восьмиполюсников
- •12 Ферритовые устройства свч
- •12.1 Физические явления в намагниченных ферритах на свч
- •12.2 Классификация устройств свч с намагниченными ферритами и их матрицы рассеяния
- •12.3 Примеры конструктивного выполнения ферритовых устройств свч
- •Контрольные вопросы:
- •Литература
Часть 1 основы теории электромагнитного поля
1 Скалярные и векторные поля. Операции над векторами
1.1 Классификация полей
Окружающий нас материальный мир можно
условно разделить на вещество и
поле. Вещество обладает массой. Поле
не имеет инертной массы. Некоторые поля
действуют на наши органы чувств
непосредственно, другие – опосредовано.
Поля делятся на скалярные и векторные.
Температурное поле является, например,
скалярным. Температура в каждой точке
жилой комнаты может быть описана
трехмерной функцией
![]() в декартовой системе координат.
Температура в комнате может быть
представлена в виде таблиц или серии
графиков. Значение температуры в каждой
точке комнаты зависит только от координаты
этой точки –
в декартовой системе координат.
Температура в комнате может быть
представлена в виде таблиц или серии
графиков. Значение температуры в каждой
точке комнаты зависит только от координаты
этой точки –
![]() и не зависит от ориентации в пространстве
регистрирующего прибора – термометра.
Это поле скалярное. Наличие напряженности
электрического поля в этой же комнате
можно зарегистрировать пробником –
вибраторной антенной. Но показания
регистратора зависят от ориентации
пробника в пространстве, так как
электрическое поле векторное и
характеризуется не только величиной,
но и направлением. Для описания векторных
полей необходимо ввести правила обращения
с векторами.
и не зависит от ориентации в пространстве
регистрирующего прибора – термометра.
Это поле скалярное. Наличие напряженности
электрического поля в этой же комнате
можно зарегистрировать пробником –
вибраторной антенной. Но показания
регистратора зависят от ориентации
пробника в пространстве, так как
электрическое поле векторное и
характеризуется не только величиной,
но и направлением. Для описания векторных
полей необходимо ввести правила обращения
с векторами.
1.2 Операции над векторами
В отличие от скалярного поля
![]() векторное поле
векторное поле
![]() задается в трехмерном пространстве в
виде трех проекций на выбранные оси
системы координат:
задается в трехмерном пространстве в
виде трех проекций на выбранные оси
системы координат:
![]() (1.1)
(1.1)
где
![]() ,
,
![]() ,
,
![]() – единичные векторы вдоль осей 0x,
0y, 0z (рисунок
1.1).
– единичные векторы вдоль осей 0x,
0y, 0z (рисунок
1.1).

Рисунок 1.1 – Прямоугольная система координат
Из (1.1) видно, что функции
![]() ,
,
![]() ,
,
![]() являются скалярными и за ориентацию и
размер вектора
являются скалярными и за ориентацию и
размер вектора
![]() отвечает комбинация трех функций.
отвечает комбинация трех функций.
Определим следующие операции над векторами.
Сложение (вычитание) векторов. При сложении векторов складываются соответствующие проекции векторов на оси системы координат:
![]()
Перемножение векторов. Различаются несколько способов перемножения векторов. Скалярное произведение единичных векторов обозначается точкой и производится по правилу (на примере единичных векторов):
![]() .
.
Векторное произведение единичных векторов обозначается крестиком или множители ставятся в квадратные скобки. Результат произведения – вектор:
![]()
Результат произведения имеет знак плюс, если индексы i, j, k соответствуют последовательности осей системы координат 0x, 0y, 0z, и знак минус, если последовательность обратная – 0x , 0z , 0y.
Дифференцирование векторов. Дифференцирование многомерной скалярной функции T приводит к векторной функции, которая называется градиентом:
![]()
Дифференцирование вектора может привести к скалярной функции, которая называется дивергенцией
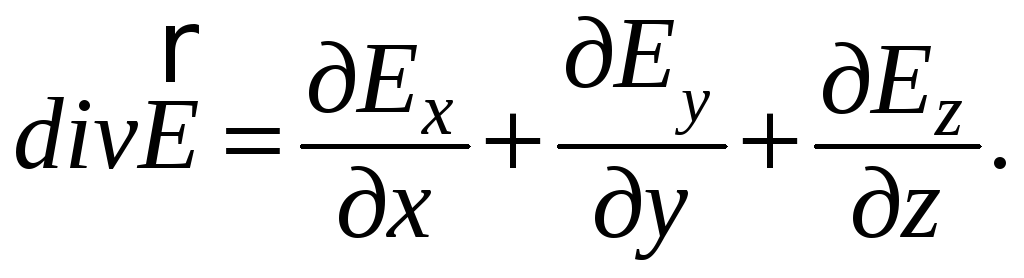
Другой способ дифференцирования вектора приводит к вектору и называется ротором. Правило дифференцирования удобно определить в виде раскрытия определителя:
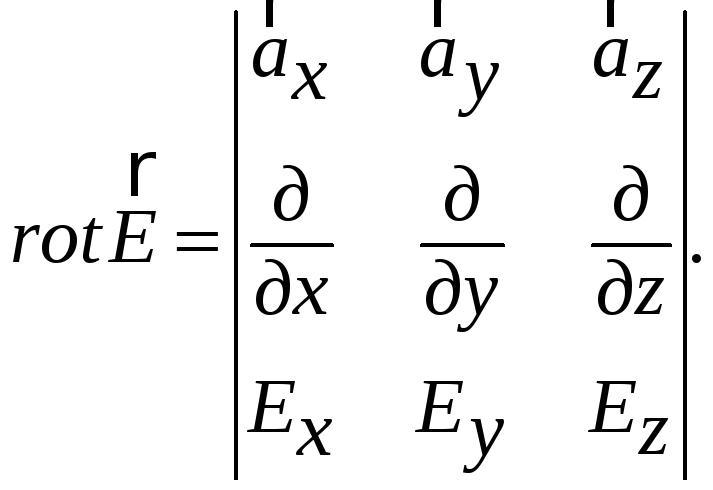
Например,
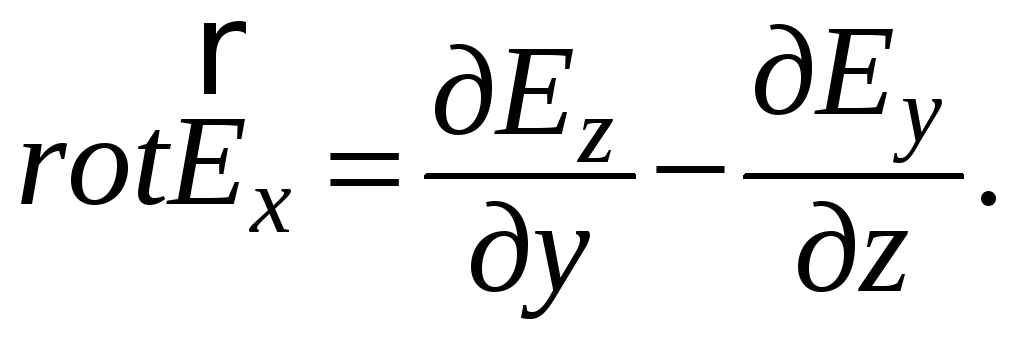
Интегрирование векторов. Одномерное
интегрирование вектора по замкнутому
контуру
![]() называется циркуляцией.
называется циркуляцией.
Интегрирование вектора по поверхности
![]() называется потоком.
называется потоком.
Теоремы Остроградского-Гаусса и Стокса устанавливают следующие соотношения:
![]() (1.2)
(1.2)
О
 пределенные
выше правила и операции над векторами
и, в частности, над единичными векторами
справедливы для любой ортогональной
системы координат [4].
пределенные
выше правила и операции над векторами
и, в частности, над единичными векторами
справедливы для любой ортогональной
системы координат [4].
y
а) б)
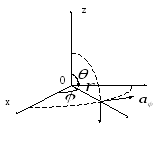
Рисунок 1.2 – Цилиндрическая и сферическая системы координат
На рисунке 1.2 показаны координаты и единичные векторы круговой цилиндрической и сферической систем координат.
Контрольные вопросы:
1 Дать определение скалярных и векторных величин.
2 Представление векторов в прямоугольной системе координат.
3 Представление векторов в круговой цилиндрической системе координат.
4 Представление векторов в сферической системе координат.
5 Определение скалярного произведения единичных векторов.
6 Определение векторного произведения единичных векторов.
7 Правая и левая тройки единичных векторов.
8 Записать оператор
![]() в прямоугольной системе координат.
в прямоугольной системе координат.
