1.2 Скалярное произведение в координатной форме
Возьмем два вектора, заданных в координатной форме :
и перемножим их
скалярно. Правые части можно перемножить
по правилу умножения многочлена на
многочлен, так как скалярное произведение
подчиняется распределительно-му закону
(свойству) :
Итак,
(2) т.е. скалярное
произведение двух векторов в
ортонормированном базисе равно сумме
парных произведений одноименных
координат этих векторов.
Для скалярного
квадрата имеем
.
Откуда модуль
(длина) вектора равен корню квадратному
из суммы квад-ратов его координат, т.е.
или
.
Согласно свойству 1 и равенству (2) можно записать условие перпенди-кулярности (ортогональности) двух векторов в координатной форме
(3)
1.3 Приложение скалярного произведения к геометрии и механике
1. Угол между двумя векторами.
Из определения
скалярного произведения
следует, что
(4)
Если векторы заданы
своими координатами в ортонормированном
ба-зисе :
, то
(5)
2. Направление вектора.
Направление вектора определяется, как было установлено, его направ-ляющими косинусами (рис. 4.2.).
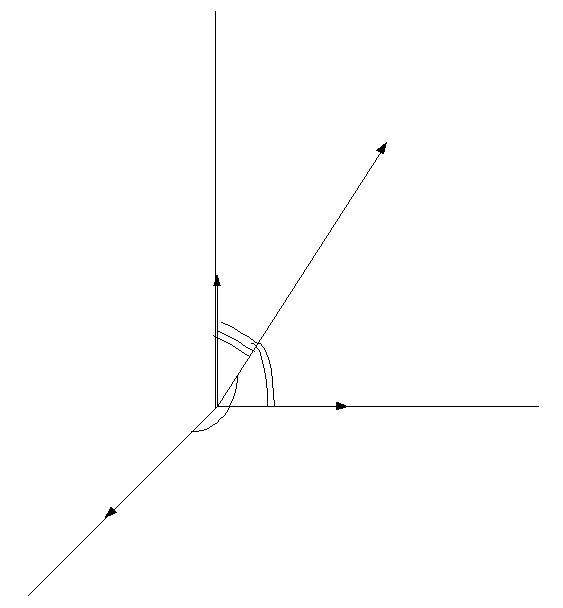
Рис. 4.2. К определению направления вектора
Положить в формулах
(4) и (5)
и отметив, что
и его коор-динаты {1;
0; 0} находим
(6)
Аналогично, взяв
и
,
получим
;
При этом
(7)
Направляющие косинусы вектора полностью определяют его направ-ление, но ничего не говорят о его длине.
Примеры :
1. Найти
угол φ между векторами
.
Решение. Искомый угол определим на основе формул (4) и (5) :
Следовательно,
угол φ=900
и векторы
и
ортогональны (перпен-дикулярны).
Выводы :
1. Скалярное произведение распространяется на случай двух векторов – сомножителей и не распространяется на случай трех сомножителей.
2. Физический
смысл
скалярного произведения заключается
в том, что скалярное произведение
численно равно работе А силы
по направ-ленному отрезку
.
3. К скалярным произведениям применяются те же преобразования, ка-кие осуществляются над произведениями многочленов («раскрытие» скобок, вынесение общего множителя).
20. Векторное произведение векторов. 2. Векторное произведение двух векторов
Определение 1.
Векторным произведением двух неколлинеарных
век-торов
и
называется такой вектор
который удовлетворяет трем условиям
(рис.4.4).
Имеет модуль
1)
;
(9)
2)
т.е. перпендикулярен к плоскости векторов
и
;
3)
направлен так, чтобы тройка векторов
,
,
бы-ла правой.
Обозначение
:
=
×
или
φ
Рис.4.4. К понятию векторного произведения.
Замечание.
1. Приведенные условия однозначно определяют векторное произведение, если сомножители – ненулевые векторы. Если хоть один из сомножителей – нулевой вектор, то векторное произведение равно нулю.
2. Модуль векторного
произведения численно равен площади
парал-лелограмма (рис. 4.4), построенного
на векторах
и
.