15.Свойства решений однородной системы линейных уравнений.
16.Структура общего решения неоднородной системы линейных уравнений. В общем случае однородная система линейных уравнений имеет вид
(22)
Однородная система всегда совместна .
Это следует из
теоремы Кронекера-Капелли, а также
очевидно, что
,
является решением системы.
Это решение называется нулевым или тривиальным .
Для однородной системы важно установить, имеет ли она ненулевое ре-шение. Ответ на этот вопрос дает следующая теорема.
Теорема 2. Для того чтобы однородная система имела ненулевое решение необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных: r(A)< n .
Следствие 1. Если в однородной системе число неизвестных n больше числа уравнений m , то система, помимо нулевого реше-ния, обладает ещё и ненулевым.
Следствие 2. Для того чтобы однородная система n линейных уравне-ний с n неизвестными обладала и ненулевыми решениями
необходимо и достаточно, чтобы равнялся нулю определитель системы.
Пример 2. Решить систему
(23)
А. Исследование системы
Решение. 1. Найдем r(A)
|
1
|
[+]
|
)
А=
I
II III
[х(-3)]
(-6
-3 -15 9 )
[+]
[
∑ ]
[ ∑ ]
2) Сложим 3-ю и 4-ю строки и эту сумму вычтем из 2-ой строки, умножен-ной на 3 (или сложим со 2-ой, умноженной на -3), получим
,
т.е. r(A)<
4 .
Отсюда r(A)= 3 , так как минор 3-го порядка
,
т.е. r(A)=
3< n
= 4 .
Следовательно, система имеет и ненулевые решения .
Замечание. Исходная система (23) эквивалентна системе (24) , которая составлена на основании выбранного минора. Конечно, можно было взять и другой минор матрицы А , если бы проделать другие преобразования над ней при определе-нии ранга.
(А в данном случае можно исключить из системы (23) вто-рое уравнение и решить систему (24)).
В. Решение системы.
2. Решим систему
(24)
Пусть х4 = t , где t - параметр, принимающий произвольное числовое значение . Решим полученную систему трех линейных уравнений с тремя неизвестными, например , по формулам Крамера.
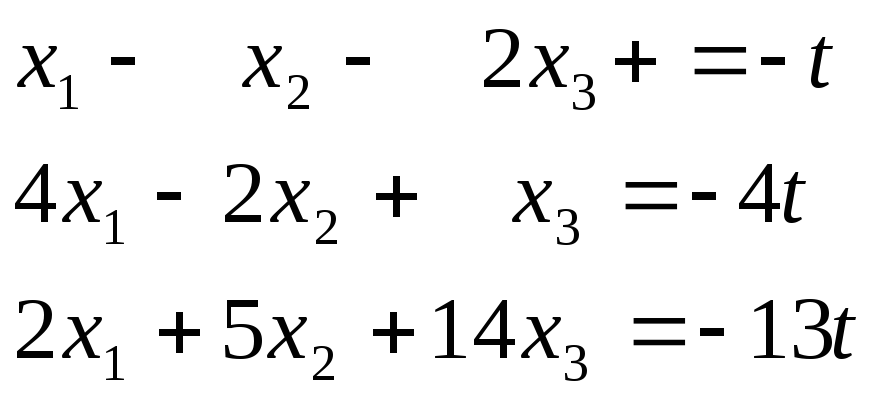
Следовательно,
Путем подстановки этого решения во все четыре уравнения системы (23) лег-ко убедиться, что система решена правильно.
17. Системы координат на плоскости.
17. Понятие вектора. Действия над векторами. Определение 1. Вектором называется направленный отрезок, или
упорядоченная пара точек.
Вектор изображается
ориентированным (направленным) отрезком,
одна из его ограничивающих точек (А)
которого есть начало,
а другая (В)
– конец
вектора (рис. 1.1). В этом случае вектор
обозначают
или
жирной бук-вой (в лекциях
).
В
В
А А
линейный масштаб
Рис.1.1. Изображение векторов
Расстояние между
началом и концом вектора называется
длиной
(модулем)
вектора. Модуль вектора обозначают
.
В матема-тике векторы обычно считаются
безразмерными, а модуль такого вектора
– безразмерным числом.
В дальнейшем мы будем рассматривать, так называемые, свободные век-торы, начало которых при параллельном переносе самого вектора можно по-мещать в любую точку пространства. В частности для свободных векторов можно обеспечить общую их начальную точку .
Вектор, модуль
которого равен нулю (начало совпадает
с концом), назы-вается нулевым
или нуль-вектором
(направление его считается произвольным).
Векторы, параллельные одной прямой, называются коллинеарными .
Векторы, расположенные в одной плоскости или параллельные одной и той же плоскости, называются компланарными .
Два вектора называются ортогональными, если они взаимно перпендикулярны.
Два вектора
называются равными,
если они имеют одинаковую длину и
одинаковое направление (
)
.
Если дан вектор
,
то вектор
называется противоположным
вектором к вектору
и обозначается -
.
Вектор, модуль
которого равен единице, называется
единичным
(или ор-том). Обычно он обозначается
.