3. Действительные числа.

3.1. Аксиомы действительных чисел.

        Множество R = {x, y, z,…} действительных чисел - множество мощности континуум, на котором определены две операции (сложение и умножение) и отношение упорядоченности (x ≤ y), удовлетворяющие аксиомам                  I.1.x + y = y + x;                  I.2.(x + y) + z = x + (y + z);                  I.3. Существует такой элемент 0∈R, что 0 + х = х для ∀х∈R;                  I.4. Для каждого элемента х∈R существует такой элемент -х, что х + (-х) = 0;

                 II.1. x·y = y·x;                  II.2. (x·y)·z = x·(y·z);                  II.3. Существует такой элемент 1∈R, что 1·х = х для ∀х∈R;                  II.4. Для каждого элемента х∈R существует такой элемент х^-1, что х·х^-1 = 1;

                 III.1. x·(y + z) = x·y + x·z;                      IV.1. Отношение {(x ≤ y)∧(y ≤ x)} эквивалентно отношению x = y;                  IV.2. Для любых двух элементов х∈R, y∈R или х ≤ у, или y ≤ x;                  IV.3. Из x ≤ y и y ≤ z следует x ≤ z;                  IV.4. Из x ≤ y следует x + z ≤ y + z для любых x, y, z ∈ R;                  IV.5. Из 0 ≤ x и 0 ≤ y следует 0 ≤ x·y;         Отношение x ≤ y записывается также в форме y ≥ x. Отношение {(x ≤ y)∧(x ≠ y)} записывается в форме х < у.                       V. Аксиома непрерывности: для любых элементов х ∈ R, y ∈ R таких, что х < у, существует элемент z ∈ R, такой что х < z < у.                       VI. Аксиома Архимеда: для любых элементов х ∈ R, y ∈ R таких, что 0 < х, 0 < у, существует такое натуральное число n, что у ≤ n·х;                       VII. Аксиома о вложенных отрезках: если {[a_n, b_n]} - счётная последовательность отрезков, таких что a_n ≤ a_n+1 и b_n+1 ≤ b_n, при ∀n, то пересечение этой последовательности непусто, т.е. ∃ х ∈ R: х∈[a_n, b_n] для ∀n.

3.2. Некоторые множества на числовой оси.

        Определения.         3.2.1. Для любой пары элементов a ∈ R, b ∈ R такой, что a < b, множество действительных чисел х, удовлетворяющей условию а < х < b, называется открытым промежутком, или интервалом с началом а и концом b и обозначается (a, b) (или ]a, b[).         3.2.2. Множество действительных чисел х, удовлетворяющей условию а ≤ х ≤ b, называется замкнутым промежутком, или отрезком и обозначается [a, b].         3.2.3. Определения полуоткрытых промежутков: (a, b] = {x| а < х ≤ b}; [a, b) = {x| а ≤ х < b}.         3.2.4. Пусть ε ∈ R, ε > 0. ε-окрестностью числа (точки) х₀ называется множество U_ε(x₀) = {x ∈ R | x₀ − ε < x < x₀ + ε} = {x ∈ R | |x - x₀| < ε}.         3.2.5. Проколотой ε-окрестностью числа (точки) х₀ называется множество         .         Пусть Х - произвольное множество действительных чисел.         3.2.6. Точка х₀ называется предельной точкой множества Х, если в любой ε-окрестности точки х₀ имеются элементы множества Х, отличные от х₀.         Предельная точка множества может принадлежать этому множеству, а может не принадлежать ему. Так, точка х₀ = 1 является предельной и для отрезка [0, 1], и для интервала (0, 1).

3.3. Несобственные точки числовой прямой.

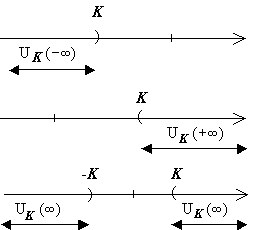
        Дополним множество вещественных чисел тремя новыми объектами (-∞, +∞, ∞), которые определим через систему их окрестностей.         Определения.         3.3.1. Несобственной точкой -∞ будем называть объект, К-окрестность которого - множество U_K(-∞) ={x| x < K}.         Для ∀у ∈ R выполняется -∞ < у.         3.3.2. Несобственной точкой +∞ будем называть объект, К-окрестность которого - множество U_K(+∞) ={x| x > K}.         Для ∀у ∈ R выполняется у < +∞.         3.3.3. Несобственной точкой ∞ будем называть объект, К-окрестность которого - множество U_K(∞) ={x| |x| > K} = U_K(-∞)∪U_K(+∞).