
- •16. Кратные, криволинейные, поверхностные интегралы.
- •16.1. Двойной интеграл.
- •16.1.3. Свойства двойного интеграла.
- •16.1.5. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •16.1.6. Задачи на двойной интеграл.
- •16.1.7. Приложения двойного интеграла.
- •16.2. Тройной интеграл.
- •16.2.2.3. Интеграл от единичной функции по области V равен объёму этой области: .
- •16.2.5. Замена переменных в тройном интеграле.
- •14.3. Несобственные кратные интегралы.
- •16.3. Криволинейные интегралы.
- •16.3.2. Криволинейный интеграл первого рода (по длине дуги).
- •16.3.2.4. Механические приложения криволинейного интеграла 1-го рода.
- •16.3.3. Криволинейный интеграл второго рода (по координатам).
- •16.3.3.4. Формула Грина.
- •16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.
- •16.4. Поверхностные интегралы.
- •16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
- •16.4.3.3. Вычисление поверхностного интеграла первого рода.
- •6.4.3.4. Механические и физические приложения поверхностного интеграла 1-го рода.
- •16.4. Поверхностные интегралы.
- •16.4.4. Поверхностный интеграл второго рода (по координатам).
- •17. Теория поля.
- •17.1. Скалярное поле.
- •17.1.2. Частные случаи скалярных полей.
- •17.2. Векторное поле.
- •17.2.2. Дифференциальные характеристики векторного поля.
- •17.2.2.1. Дивергенция векторного поля.
- •17.2.3. Частные случаи векторных полей.
- •17.3.Поток векторного поля через поверхность.
16. Кратные, криволинейные, поверхностные интегралы.
16.1. Двойной интеграл.
 16.1.1.
Определение двойного интеграла.
Теорема
существования двойного интеграла. Пусть
на плоскости Oxy
задана ограниченная замкнутая область
D
с кусочно-гладкой границей, и пусть на
области D
определена функция
16.1.1.
Определение двойного интеграла.
Теорема
существования двойного интеграла. Пусть
на плоскости Oxy
задана ограниченная замкнутая область
D
с кусочно-гладкой границей, и пусть на
области D
определена функция ![]() .
.
Разобьём область
D
произвольным образом на ![]() подобластей
подобластей ![]() (не имеющих общих внутренних точек).
Символом
(не имеющих общих внутренних точек).
Символом ![]() будем обозначать площадь области
будем обозначать площадь области ![]() ;
символом
;
символом
![]() здесь и дальше будет обозначаться
наибольшее расстояние между двумя
точками, принадлежащими области D:
здесь и дальше будет обозначаться
наибольшее расстояние между двумя
точками, принадлежащими области D:
![]() ;
;
символом ![]() обозначим наибольший из диаметров
областей
обозначим наибольший из диаметров
областей ![]() :
:
![]() .
.
В каждой из
подобластей ![]() выберем произвольную точку
выберем произвольную точку ![]() ,
вычислим в этой точке значение функции
,
вычислим в этой точке значение функции
![]() ,
и составим интегральную сумму
,
и составим интегральную сумму ![]() .
.
Если существует
предел последовательности интегральных
сумм при ![]() ,
не зависящий ни от способа разбиения
области D
на подобласти
,
не зависящий ни от способа разбиения
области D
на подобласти ![]() ,
ни от выбора точек
,
ни от выбора точек ![]() ,
то функция
,
то функция ![]() называется интегрируемой по области
D,
а значение этого предела называется
двойным интегралом от функции
называется интегрируемой по области
D,
а значение этого предела называется
двойным интегралом от функции ![]() по области D
и обозначается
по области D
и обозначается
![]() .
.
Если расписать
значение ![]() через координаты точки
через координаты точки ![]() ,
и представить
,
и представить ![]() как
как ![]() ,
получим другое обозначение двойного
интеграла:
,
получим другое обозначение двойного
интеграла:
![]() .
Итак, кратко,
.
Итак, кратко,
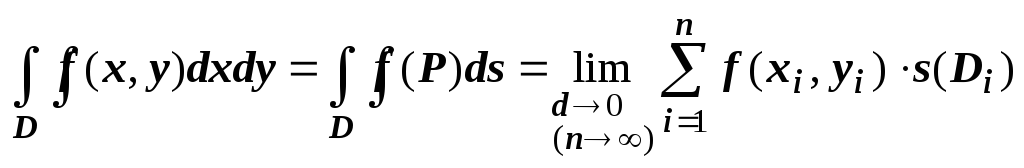 .
.
Теорема
существования двойного интеграла. Если
подынтегральная функция ![]() непрерывна на области D,
то она интегрируема по этой области.
непрерывна на области D,
то она интегрируема по этой области.
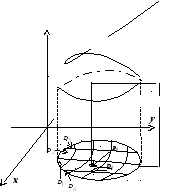
16.1.2. Геометрический
смысл двойного интеграла. Геометрический
смысл каждого слагаемого интегральной
суммы: если
![]() ,
то
,
то ![]() - объём прямого цилиндра с основанием
- объём прямого цилиндра с основанием
![]() высоты
высоты ![]() ;
вся интегральная сумма
;
вся интегральная сумма ![]() - сумма объёмов таких цилиндров, т.е.
объём некоторого ступенчатого тела
(высота ступеньки, расположенной над
подобластью
- сумма объёмов таких цилиндров, т.е.
объём некоторого ступенчатого тела
(высота ступеньки, расположенной над
подобластью ![]() ,
равна
,
равна ![]() ).
Когда
).
Когда ![]() ,
это ступенчатое тело становится всё
ближе к изображенному на рисунке телу,
ограниченному снизу областью
,
это ступенчатое тело становится всё
ближе к изображенному на рисунке телу,
ограниченному снизу областью ![]() ,
сверху - поверхностью
,
сверху - поверхностью ![]() ,
с цилиндрической боковой поверхностью,
направляющей которой является граница
области
,
с цилиндрической боковой поверхностью,
направляющей которой является граница
области ![]() ,
а образующие параллельны оси
,
а образующие параллельны оси ![]() .
Двойной интеграл
.
Двойной интеграл
![]() равен объёму этого тела.
равен объёму этого тела.
16.1.3. Свойства двойного интеграла.
16.1.3.1. Линейность. Если функции
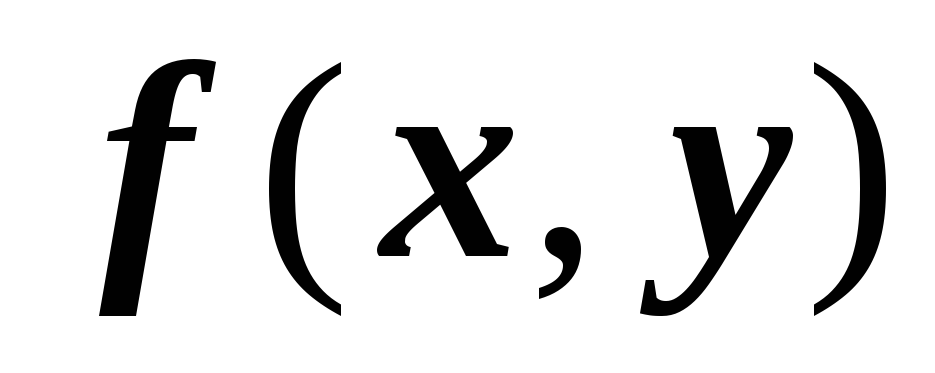 ,
,
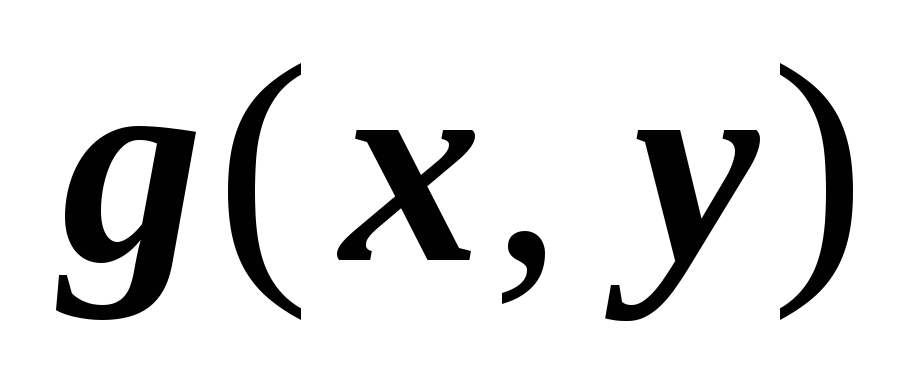 интегрируемы по области
интегрируемы по области 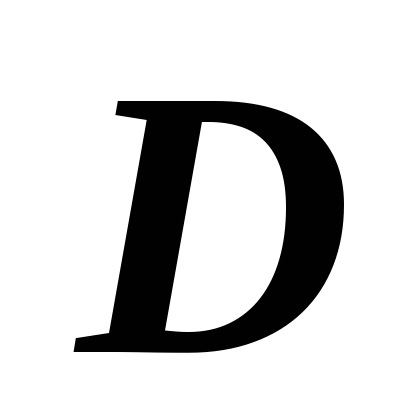 ,
то их линейная комбинация
,
то их линейная комбинация 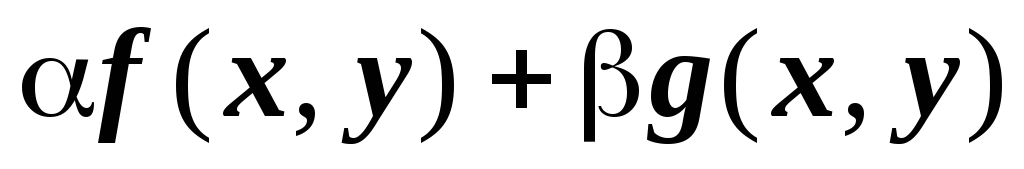 тоже интегрируема по области
тоже интегрируема по области 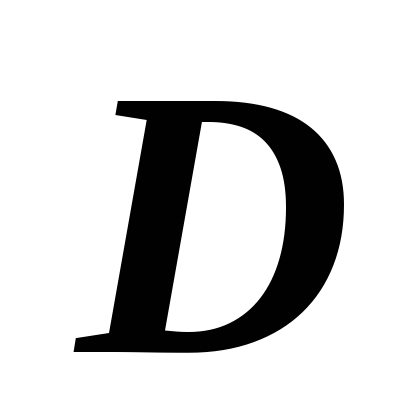 ,
и
,
и
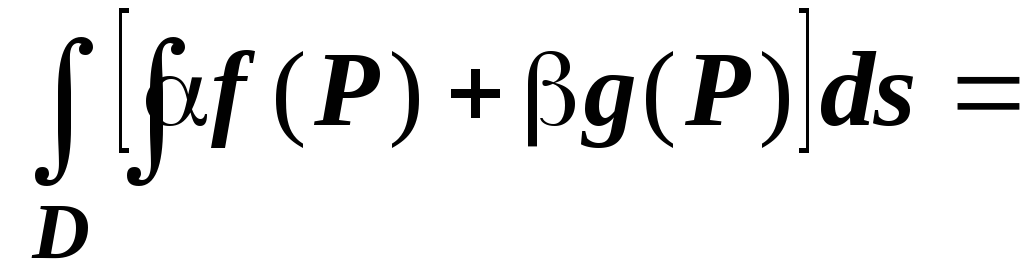
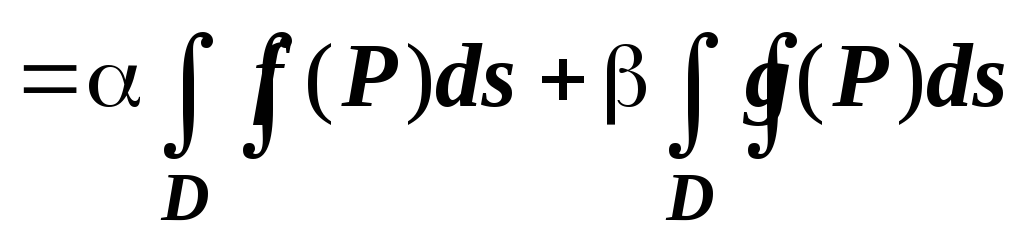 .
.
Док-во. Для
интегральных сумм справедливо равенство
![]()
![]() .
Переходя к пределу при
.
Переходя к пределу при ![]() и пользуясь свойствами пределов,
рассмотренными в разделе 4.4.6.
Арифметические действия с пределами
(конкретно, свойствами 4.4.10.1 и 4.4.10.2),
получим требуемое равенство.
и пользуясь свойствами пределов,
рассмотренными в разделе 4.4.6.
Арифметические действия с пределами
(конкретно, свойствами 4.4.10.1 и 4.4.10.2),
получим требуемое равенство.
16.1.3.2. А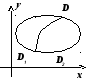 ддитивность.
Если область
ддитивность.
Если область ![]() является объединением двух областей
является объединением двух областей ![]() и
и ![]() ,
не имеющих общих внутренних точек, то
,
не имеющих общих внутренних точек, то
![]() .
.
Док-во. Пусть
область ![]() разбита на подобласти
разбита на подобласти ![]() ,
область
,
область ![]() разбита на подобласти
разбита на подобласти ![]() .
Тогда объединение этих разбиений даст
разбиение области
.
Тогда объединение этих разбиений даст
разбиение области ![]() :
:
![]() на
на ![]() подобластей. Интегральная сумма по
области
подобластей. Интегральная сумма по
области ![]() равна сумме сумм по областям
равна сумме сумм по областям ![]() и
и ![]() :
:
 .
Как и в предыдущем случае, переходя к
пределу при
.
Как и в предыдущем случае, переходя к
пределу при ![]() ,
получим требуемое равенство.
,
получим требуемое равенство.
Интеграл от единичной функции по области
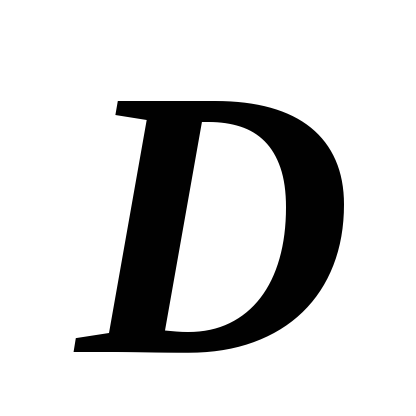 равен
площади этой области:
равен
площади этой области:
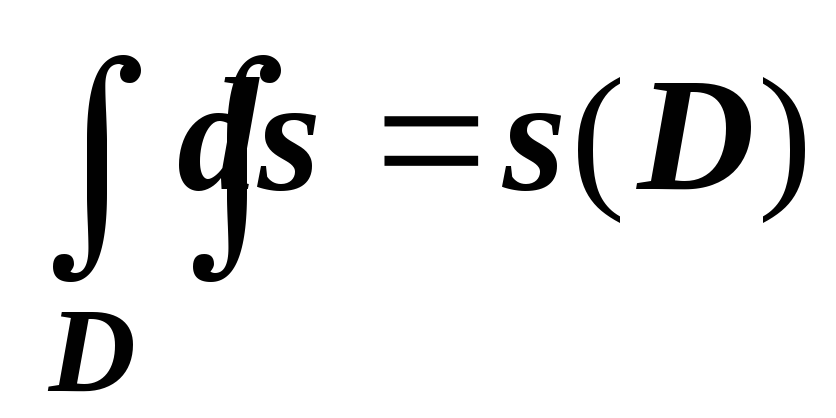 .
.
Док-во: Для
любого разбиения ![]() ,
т.е. не зависит ни от разбиения, ни от
выбора точек
,
т.е. не зависит ни от разбиения, ни от
выбора точек ![]() .
Предел постоянной равен этой постоянной,
поэтому
.
Предел постоянной равен этой постоянной,
поэтому
![]() .
.
16.1.3.4. Интегрирование
неравенств.
Если в любой точке ![]() выполняется неравенство
выполняется неравенство ![]() ,
и функции
,
и функции ![]() интегрируемы по области
интегрируемы по области ![]() ,
то
,
то
![]() .
.
Док-во.
В любой точке
![]() выполняется неравенство
выполняется неравенство
![]() ,
поэтому
,
поэтому ![]() .
По теореме о переходе к пределу в
неравенствах отсюда следует требуемое
утверждение.
.
По теореме о переходе к пределу в
неравенствах отсюда следует требуемое
утверждение.
Теоремы об оценке интеграла.
16.1.3.5.1.
Если функция ![]() интегрируема по области
интегрируема по области ![]() ,
и для
,
и для ![]() выполняется
выполняется ![]() ,
то
,
то ![]() .
.
Док-во. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (цифрами над знаками импликации обозначены
номера применяемых ранее доказанных
свойств).
(цифрами над знаками импликации обозначены
номера применяемых ранее доказанных
свойств).
16.1.3.5.2.
Если функция ![]() интегрируема по области
интегрируема по области ![]() ,
то
,
то ![]() .
.
Док-во. Эти
неравенства непосредственно следуют
из того, что ![]() и свойства 16.1.3.4.
Интегрирование неравенств.
и свойства 16.1.3.4.
Интегрирование неравенств.
16.1.3.6. Теорема о
среднем. Если
функция ![]() непрерывна на области
непрерывна на области ![]() ,
то существует точка
,
то существует точка ![]() ,
такая что
,
такая что ![]() .
.
Док-во.
Непрерывная на ограниченной замкнутой
области ![]() функция
функция ![]() принимает в некоторых точках этой
области своё минимальное
принимает в некоторых точках этой
области своё минимальное ![]() и максимальное
и максимальное ![]() значения. Так как
значения. Так как ![]() ,
то
,
то ![]() ,
или
,
или ![]() .
Непрерывная функция принимает, кроме
того, любое значение, заключённое между
.
Непрерывная функция принимает, кроме
того, любое значение, заключённое между
![]() и
и ![]() ,
в частности, значение
,
в частности, значение
![]() .
Следовательно,
.
Следовательно, ![]() ,
откуда и следует доказываемое утверждение.
,
откуда и следует доказываемое утверждение.
Вычисление двойного интеграла. Двукратный (повторный) интеграл.
Определение простой (правильной) области. Область
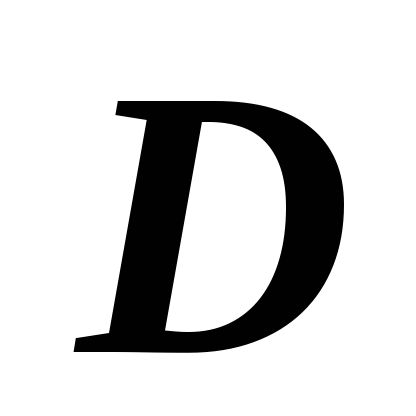 на плоскости Oxy
будем
называть простой
(правильной) в направлении оси
Oy,
если любая прямая, проходящая через
внутреннюю точку области
на плоскости Oxy
будем
называть простой
(правильной) в направлении оси
Oy,
если любая прямая, проходящая через
внутреннюю точку области 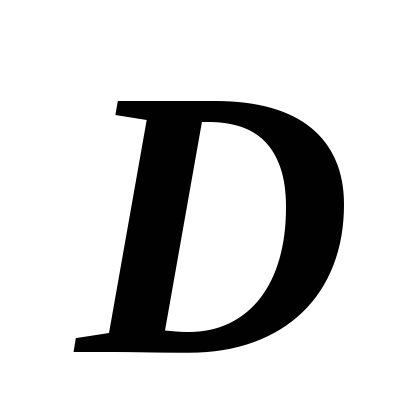 и параллельная оси Oy,
пересекает границу
и параллельная оси Oy,
пересекает границу 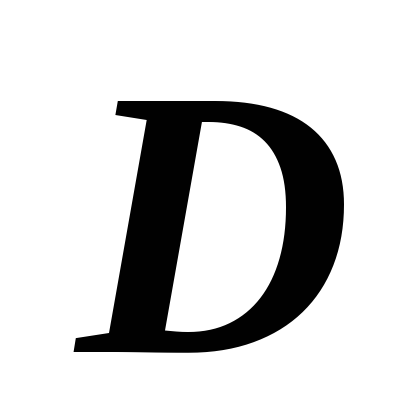 в двух точках.
в двух точках.
Аналогично
определяется область, простая
(правильная) в направлении оси Ox:
любая прямая, проходящая через внутреннюю
точку области ![]() и параллельная оси Oх,
пересекает границу
и параллельная оси Oх,
пересекает границу ![]() в двух точках.
в двух точках.
Область, правильную (простую) в направлении обеих осей, будем называть правильной.
О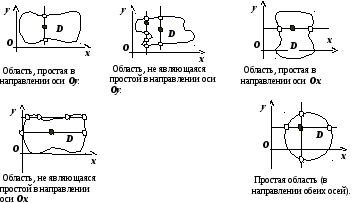
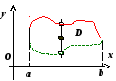 граниченную
замкнутую область
граниченную
замкнутую область![]() ,
правильную в направлении оси Oy,
можно описать неравенствами
,
правильную в направлении оси Oy,
можно описать неравенствами
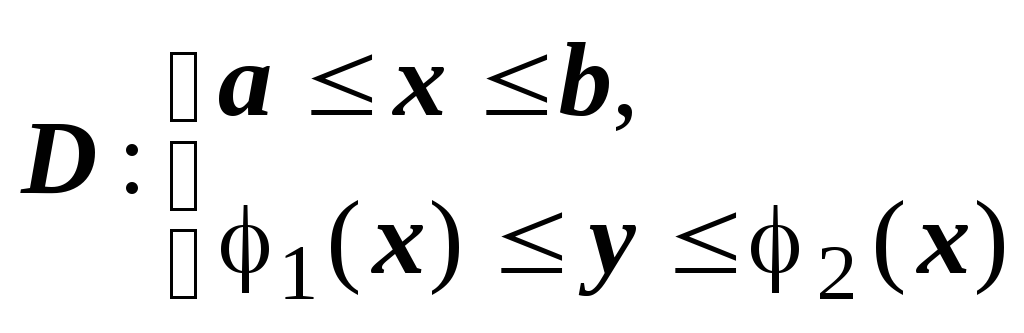 .
Числа
.
Числа
![]() и
и
![]() существуют вследствие ограниченности
области
существуют вследствие ограниченности
области ![]() ,
функция
,
функция ![]() образована нижними точками пересечения
прямой
образована нижними точками пересечения
прямой ![]() при
при ![]() с границей области
с границей области ![]() ,
функция
,
функция ![]() - верхними точками пересечения этой
прямой с границей области
- верхними точками пересечения этой
прямой с границей области ![]() :
:
Аналогичным
образом область ![]() ,
ограниченную, замкнутую и правильную
в направлении оси Oх,
можно описать неравенствами
,
ограниченную, замкнутую и правильную
в направлении оси Oх,
можно описать неравенствами
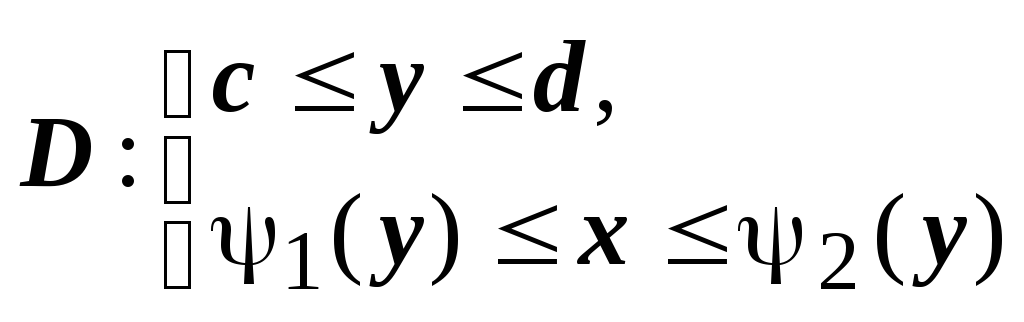 .
Функция
.
Функция ![]() образована левыми точками пересечения
прямой
образована левыми точками пересечения
прямой ![]() при
при ![]() с границей области
с границей области ![]() ,
функция
,
функция ![]() - правыми точками пересечения этой
прямой с границей области
- правыми точками пересечения этой
прямой с границей области ![]() .
.
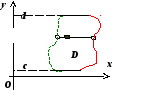 Для
правильной области (т.е. области,
правильной в направлении обеих осей)
существуют оба способа представления:
и
Для
правильной области (т.е. области,
правильной в направлении обеих осей)
существуют оба способа представления:
и
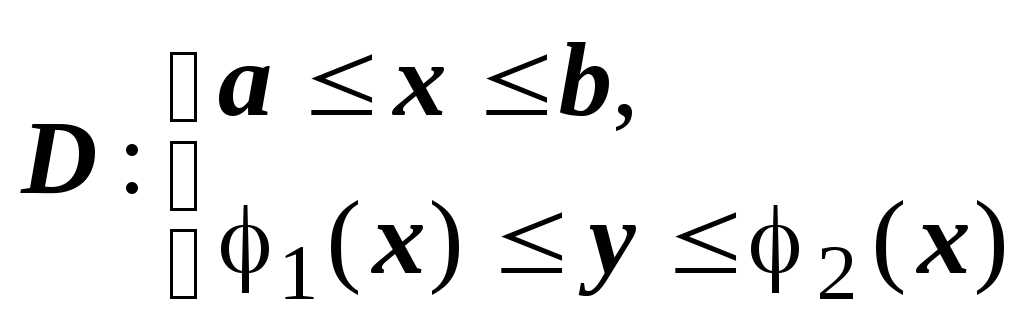 ,
и
,
и
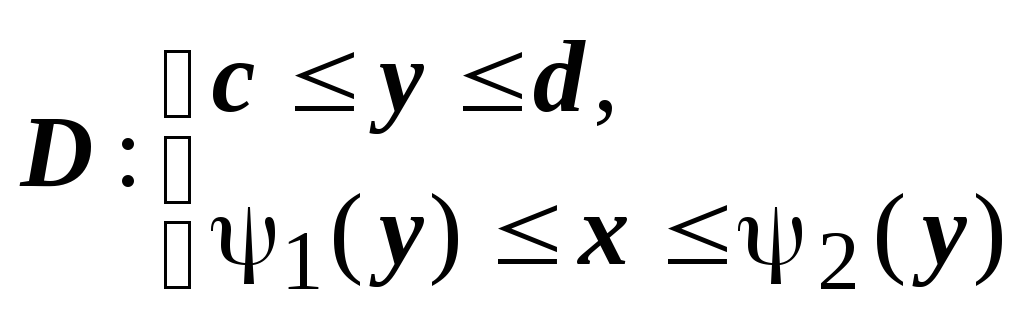 .
.
Двукратный (повторный) интеграл. Пусть
 - область, простая в направлении оси
Oy.
Рассмотрим выражение
- область, простая в направлении оси
Oy.
Рассмотрим выражение 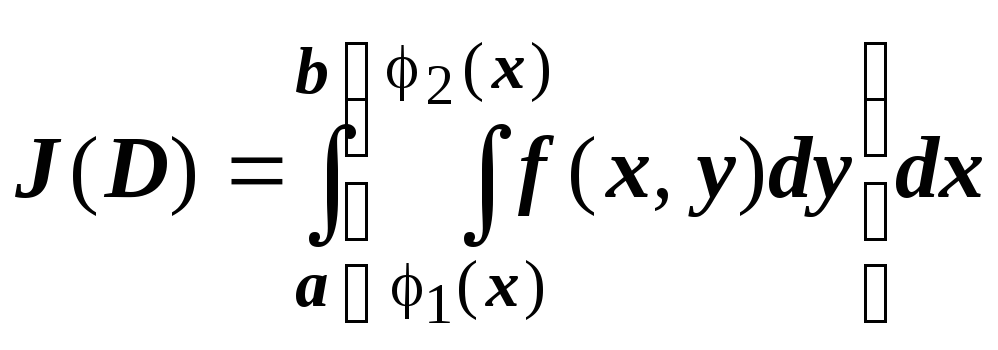 .
Эта конструкция определяется через
два обычных определённых интеграла.
После интегрирования по у
во внутреннем интеграле (переменная
х
при этом рассматривается как постоянная)
и подстановки по у
в пределах от
.
Эта конструкция определяется через
два обычных определённых интеграла.
После интегрирования по у
во внутреннем интеграле (переменная
х
при этом рассматривается как постоянная)
и подстановки по у
в пределах от 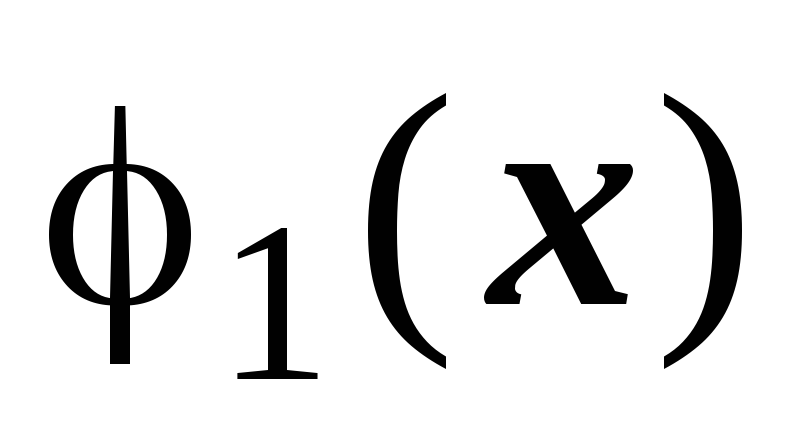 до
до 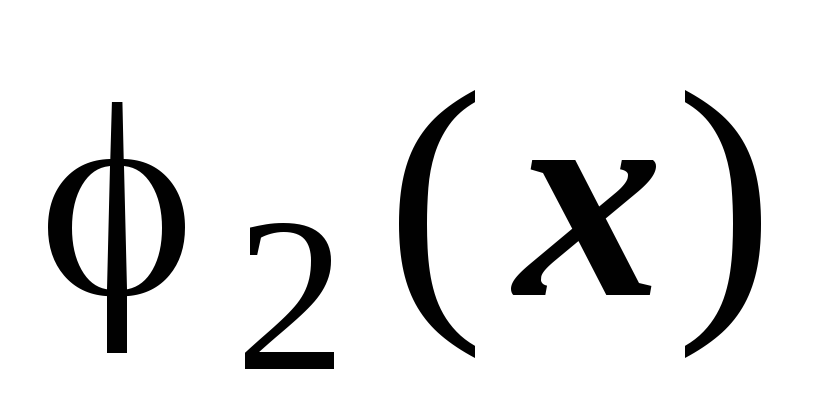 получается функция, зависящая только
от х,
которая интегрируется в пределах от
a
до b.
В дальнейшем мы будем обычно записывать
этот объект без внутренних скобок:
получается функция, зависящая только
от х,
которая интегрируется в пределах от
a
до b.
В дальнейшем мы будем обычно записывать
этот объект без внутренних скобок:
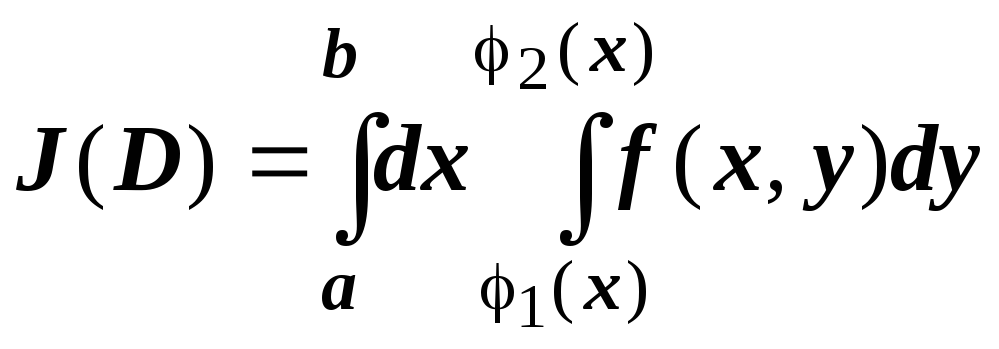 .
.
Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:
Свойства линейности
и интегрирования неравенств следуют
из этих свойств определённого интеграла;
интеграл от единичной функции даёт
площадь области![]() :
:
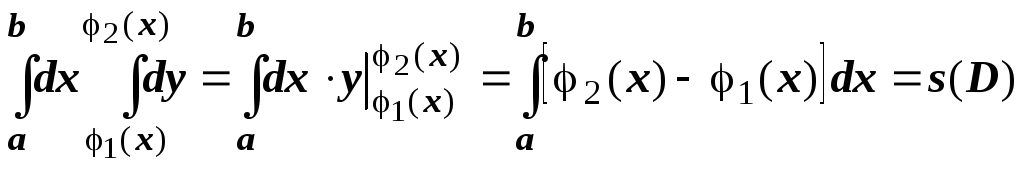 ;
;
т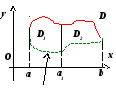 еоремы
об оценке и о среднем следуют из
перечисленных свойств. Единственное
свойство, с которым придётся повозиться
- это свойство аддитивности. Мы докажем
его в простой, но достаточной для нас
форме: если область
еоремы
об оценке и о среднем следуют из
перечисленных свойств. Единственное
свойство, с которым придётся повозиться
- это свойство аддитивности. Мы докажем
его в простой, но достаточной для нас
форме: если область![]() разбита на две подобласти
разбита на две подобласти ![]() и
и
![]() прямой, параллельной одной из координатных
осей, то двукратный интеграл по области
прямой, параллельной одной из координатных
осей, то двукратный интеграл по области
![]() равен сумме интегралов по
равен сумме интегралов по ![]() и
и
![]() :
:
![]() .
.
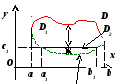 Первый
случай: прямая
Первый
случай: прямая![]() параллельна оси Oy.
Тогда
параллельна оси Oy.
Тогда 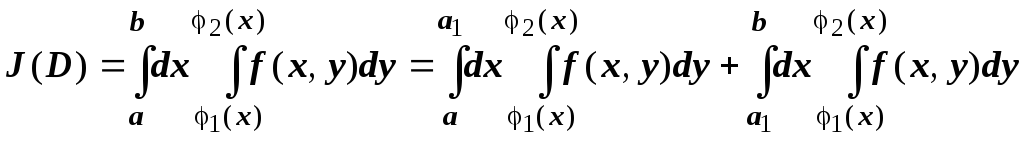 (аддитивность внешнего интеграла)
(аддитивность внешнего интеграла) ![]() .
.
Второй случай:
прямая ![]() параллельна оси Oх.
Воспользуемся сначала аддитивностью
внешнего интеграла:
параллельна оси Oх.
Воспользуемся сначала аддитивностью
внешнего интеграла: 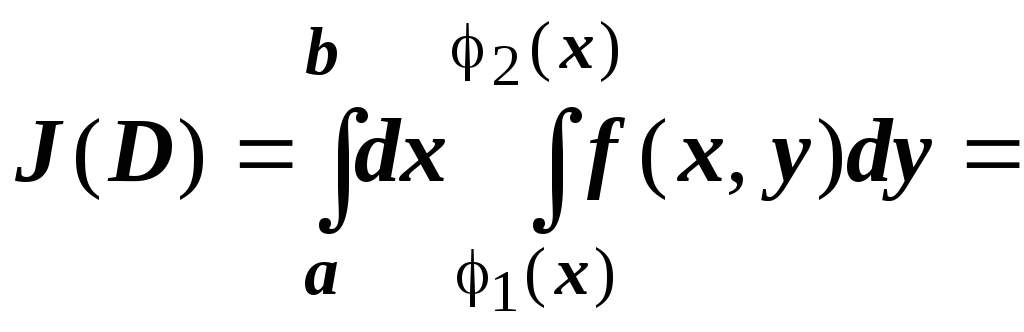
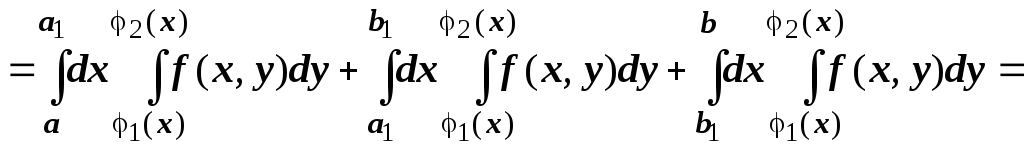
![]()
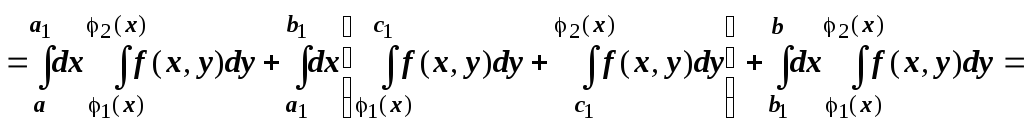 (применяем свойство
линейности для внешнего интеграла в
среднем слагаемом и перегруппировываем
сумму)=
(применяем свойство
линейности для внешнего интеграла в
среднем слагаемом и перегруппировываем
сумму)=
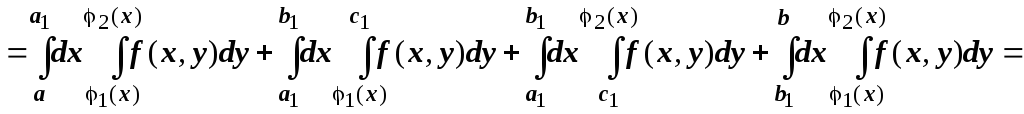
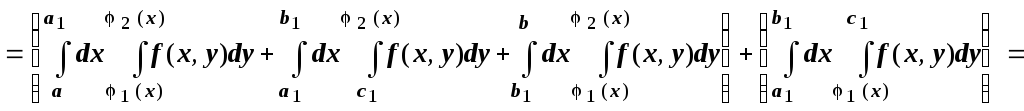
(первая фигурная
скобка даёт повторный интеграл по ![]() ,
второй - по
,
второй - по
![]() )
)
![]() .
.
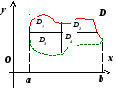 Понятно,
что воэможны различные случаи взаимного
расположения прямых
Понятно,
что воэможны различные случаи взаимного
расположения прямых![]() ,
,
![]() ,
,
![]() и функций
и функций ![]() ,
,
![]() ,
но логика доказательства во всех случаях
такая же.
,
но логика доказательства во всех случаях
такая же.
Обобщим доказанное
свойство. Пусть прямая разбивает область
![]() на две подобласти
на две подобласти ![]() и
и ![]() .
Проведём ещё одну прямую, параллельную
какой-либо координатной оси. Пусть эта
прямая разбивает
.
Проведём ещё одну прямую, параллельную
какой-либо координатной оси. Пусть эта
прямая разбивает ![]() на
на ![]() и
и![]() ;
;
![]() - на
- на ![]() и
и ![]() .
По доказанному,
.
По доказанному, ![]() ,
,
![]() ,
поэтому
,
поэтому ![]() .
Продолжая рассуждать также, убеждаемся
в справедливости следующего утверждения:
если область
.
Продолжая рассуждать также, убеждаемся
в справедливости следующего утверждения:
если область ![]() с помощью прямых, параллельных координатным
осям, разбита на подобласти
с помощью прямых, параллельных координатным
осям, разбита на подобласти ![]() ,
то
,
то ![]() .
.
Теорема о переходе от двойного интеграла к повторному. Пусть
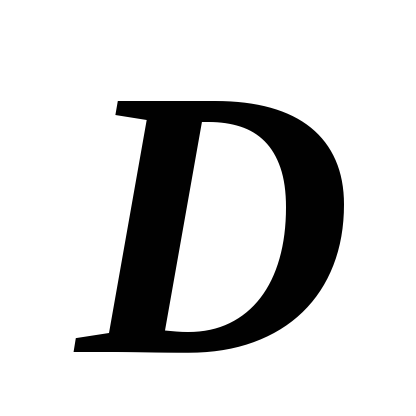 - простая в направлении оси Oy
область. Тогда двойной интеграл от
непрерывной функции по области
- простая в направлении оси Oy
область. Тогда двойной интеграл от
непрерывной функции по области 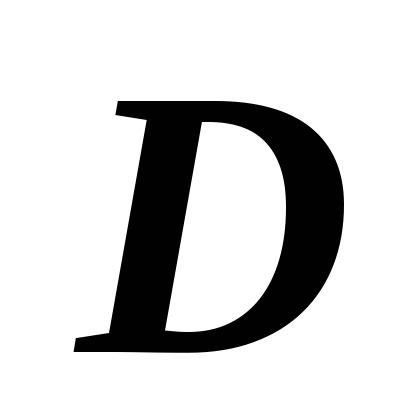 равна повторному интегралу от той же
функции по области
равна повторному интегралу от той же
функции по области 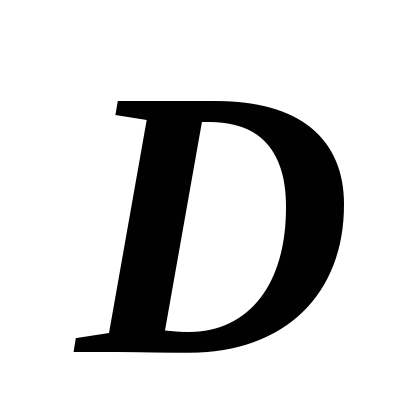 :
:
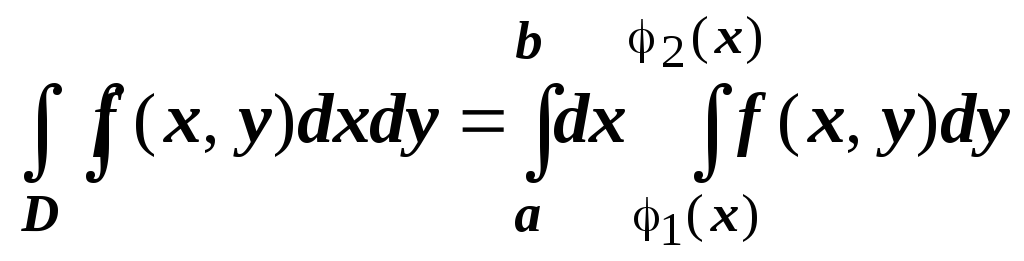 .
.
Док-во.
Разобьём область ![]() с помощью прямых, параллельных координатным
осям, на подобласти
с помощью прямых, параллельных координатным
осям, на подобласти ![]() .
По доказанному выше,
.
По доказанному выше,
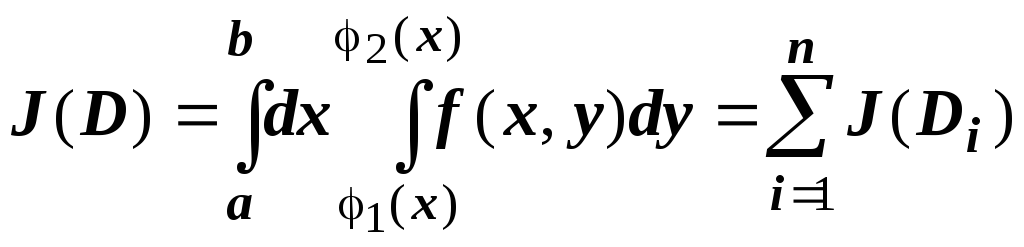 .
К каждому из итегралов
.
К каждому из итегралов
![]() применим теорему о среднем: в любой
области
применим теорему о среднем: в любой
области ![]() найдётся точка
найдётся точка ![]() такая, что
такая, что
![]() .
Следовательно,
.
Следовательно,
![]() .
В последнем равенстве справа стоит
интегральная сумма для двойного интеграла
.
В последнем равенстве справа стоит
интегральная сумма для двойного интеграла
![]() .
Будем мельчить разбиение области так,
чтобы
.
Будем мельчить разбиение области так,
чтобы ![]() .
Вследствие непрерывности функции
.
Вследствие непрерывности функции ![]() по теореме существования интегральная
сумма при этом стремится к двойному
интегралу
по теореме существования интегральная
сумма при этом стремится к двойному
интегралу
![]() ,
т.е. в пределе получим
,
т.е. в пределе получим
 ,
что и требовалось доказать.
,
что и требовалось доказать.
Если область
![]() правильная
в направлении оси Oх,
то аналогично доказывается формула
правильная
в направлении оси Oх,
то аналогично доказывается формула
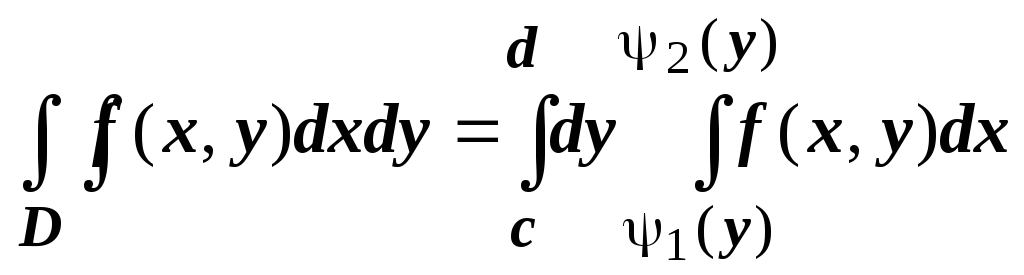 .
Если
.
Если ![]() правильна
в направлении обеих осей, то для вычисления
двойного интеграла можно применять
любую из эти формул:
правильна
в направлении обеих осей, то для вычисления
двойного интеграла можно применять
любую из эти формул:
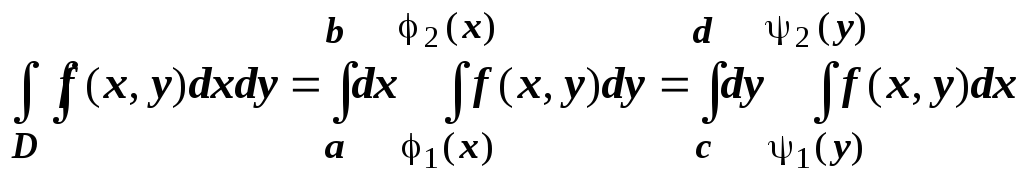 .
.
Если область не является правильной, её разбивают на правильные подобласти.
