pp1. Принцип вложенных отрезков (Коши-Кантора).

Формулировка

Для всякой системы вложенных отрезков

существует хотя бы одна точка  , принадлежащая всем отрезкам данной системы.

Если, кроме того, длина отрезков системы стремится к нулю:

то   — единственная общая точка всех отрезков данной системы.

Доказательство

1) Существование общей точки. Множество левых концов отрезков   лежит на числовой прямой левее множества правых концов отрезков  , поскольку

В силу аксиомы непрерывности, существует точка  , разделяющая эти два множества, то есть

в частности («От пр.» an>bm, => an<=bn,bm=>am, => am<=bm<an<=bn, => an<=bm.)

Последнее неравенство означает, что   — общая точка всех отрезков данной системы.

2) Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки   и  , принадлежащие всем отрезкам системы:

Тогда для всех номеров   выполняются неравенства:

В силу условия стремления к нулю длин отрезков для любого   для всех номеров  , начиная с некоторого будет выполняться неравенство

Взяв в этом неравенстве  , получим

Противоречие. Лемма доказана полностью.

Аксиома непрерывности (полноты). Каковы бы ни были непустые множества   и  , такие что для любых двух элементов   и   выполняется неравенство  , существует такое число  , что для всех   и   имеет место соотношение

2. Теорема о существовании точной верхней (нижней) грани ограниченного числового

множества.

Определение. Если для подмножества       :    , то множество   называется ограниченным сверху, а число   - числом, ограничивающим сверху множество  .

Множество   ограниченно сверху             :  .

Определение. Множество, не являющееся ограниченным сверху множеством, называется неограниченным сверху множеством.

Множество   не ограниченно сверху  .

Определение. Если для подмножества  , то множество   называется ограниченным снизу, а число   - числом, ограничивающим снизу множество  .

Множество   ограниченно снизу  .

Определение. Множество, не являющееся ограниченным снизу множеством, называется неограниченным снизу множеством.

Множество   не ограниченно снизу  .

Определение. Множество, ограниченное и сверху и снизу, называется ограниченным множеством.

Определение. Множество, не являющееся ограниченным, называется не ограниченным множеством.

Определение. Наименьшее среди всех чисел, ограничивающих сверху множество  , называется его верхней гранью и обозначается через   или  .

 - верхняя грань множества   и  .

Определение. Наибольшее среди всех чисел, ограничивающих снизу множество  , называется его нижней гранью и обозначается через   или  .

 - нижняя грань множества   и  .

Пример.  , где  .

Теорема.   ограниченное сверху непустое числовое множество имеет верхнюю грань, а всякое ограниченное снизу непустое числовое множество имеет нижнюю грань.

Доказательство. Пусть   - ограниченное сверху непустое числовое множество. Обозначим через   множество всех чисел, ограничивающих сверху множество  . Множество   ограничено сверху, поэтому множество   не пусто. Каждый элемент   ограничивает сверху множество  , т.е.  . Элементы  и   являются произвольными элементами соответственно множеств   и  , поэтому, в силу свойства непрерывности действительных чисел,   и  имеет место неравенство  .

Выполнение неравенства   означает, что число   ограничивает сверху множество  , а выполнение неравенства   для всех   , т.е. для всех чисел, ограничивающих сверху множество  , означает, что число   является наименьшим среди всех таких чисел, т.е. верхней гранью множества  :  .

-е верхней грани у ограниченного сверху непустого множества доказано.

Если теперь   - непустое ограниченное снизу числовое множество, то отнесём к множеству   все числа, ограничивающие снизу множество  .

Аналогично рассмотренному случаю верхней грани, легко убеждаемся, что, в силу свойства неперрывности действительных чисел,   и   имеет место неравенство  .

Это означает, что   Теорема доказана.

3. Теорема о единственности предела числовой последовательности.

2. Определение предела последовательности.

Определение. Число а называется пределом последовательнос­ти , если для каждого существует такой номер , что для всех выполняется неравенство  Если а — предел последовательности, то пишут   или  при  С помощью логических символов это определение можно записать в виде   (1) Последовательность, у которой существует предел, называют схо­дящейся. Таким образом, последовательность   является сходящейся, если :  (2) Последовательность, не являющуюся сходящейся, называют рас­ходящейся.; иначе говоря, последовательность называют расходящей­ся, если никакое число не является ее пределом. Заметим, что если для всех (такую последователь­ность называют стационарной), то Из определения (1) следует, что последовательность имеет предел, равный а, тогда и только тогда, когда последовательность  имеет предел, равный нулю, т. е. 

3. Единственность предела последовательности. Теорема 1. Числовая последовательность может иметь только один предел. Предположим, что последовательность имеет два различных предела а и b, причем (рис. 4.2). Выберем таким, чтобы

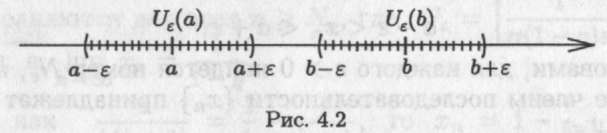
е-окрестности точек а и b не пересекались (не имели общих точек). Возьмем, например, Так как число а — предел после­довательности , то по заданному   можно найти номер N,такой, что   для всех   Поэтому вне интервала  может оказаться лишь конечное число членов последовательности. В частности, интервал может содержать лишь конечное число членов последовательности. Это противоречит тому, что Ь — предел последовательности (любая окрестность точки Ь должна содержать бесконечное число членов последовательности). Полученное противо­речие показывает, что последовательность не может иметь два раз­личных предела. Итак, сходящаяся последовательность имеет только один предел.

4. Теорема об ограниченности сходящейся числовой последовательности.

Доказательство. Пусть   – сходящаяся к числу а, тогда  , где  . Так как бесконечно малая последовательность ограничена, то существует такое число  , что для всех   выполняется  . Поэтому   для всех  , а это и означает, что последовательность   ограничена.

5. Теорема Вейерштрасса о сходимости монотонной ограниченной последовательности.

Доказательство. Докажем теорему для монотонной возрастающей последовательности  . Докажем, что точная верхняя граница для последовательности   и будет ее пределом.

Действительно, по определению точной верхней границы

Кроме того, какое бы ни взять число  , найдется такой номер  , что

Так как последовательность монотонна, то при   будет  , а значит, и   и выполняются неравенства

откуда и следует, что  .

6. ???????????????????

7. Предельная точка числового множества и ее свойства. Лемма о предельной точке.

В частности, предельной точкой числового множества, имеющего бесконечное число элементов, называется точка числовой прямой, в любой окрестности которой содержится бесконечно много элементов этого множества. Также можно считать предельной точкой такого множества  , если из некоторых его элементов можно составить бесконечно большую последовательность с попарно различными отрицательными элементами. Если же можно составить бесконечно большую последовательность с попарно различными положительными элементами, то можно считать предельной точкой  .^[1]

Верхняя предельная точка числового множества — это наибольшая из его предельных точек.

Нижняя предельная точка числового множества — это наименьшая из его предельных точек.

[Править]Свойства

• У любого ограниченного числового множества, имеющего бесконечное число элементов, существуют и верхняя, и нижняя предельные точки (в множествевещественных чисел). Если добавить в множество вещественных чисел   и  , то в получившемся множестве предельные точки имеют вообще все числовые множества с бесконечным числом элементов.

• Из элементов любого ограниченного числового множества, имеющего бесконечное число элементов, можно выделить сходящуюся последовательность, элементы которой попарно различны.

Поскольку множество (назовём его  ) ограничено, то существует отрезок  , включающий  . Предположим, что ни одна точка этого отрезка не является предельной для  . Тогда окрестностями всех точек этого множества можно покрыть весь отрезок. Значит, по принципу Бореля-Лебега, из множества этих окрестностей (коих бесконечное число, так как во множестве   по условию число элементов бесконечно) можно выделить конечное подпокрытие   какими-то окрестностями  . В каждой из этих окрестностей по условию конечное число элементов, всего окрестностей также конечное число, значит, всего в  конечное число элементов, что противоречит условию. Стало быть, у   действительно есть предельная точка.

8. Предельная точка числовой последовательности и ее свойства. Критерий сходимости

числовой последовательности, связанный с существованием предельной точки. ?????????

Предельная точка последовательности — это точка, в любой окрестности которой содержится бесконечно много элементов этой последовательности.^[1]

 — предельная точка последовательности 

Наибольшая предельная точка последовательности называется её верхним пределом, а наименьшая предельная точка — нижним пределом.

Иногда в множество возможных предельных точек включают « » и « ». Так если из последовательности можно выделить бесконечно большую подпоследовательность, все элементы которой отрицательны, то говорят, что « » является предельной точкой этой последовательности. Если же из последовательности можно выделить бесконечно большую подпоследовательность с исключительно положительными элементами, то говорят, что « » является её предельной точкой.^[1] При этом, разумеется, у последовательности могут быть и другие предельные точки.

[Править]Свойства

• Точка является предельной точкой последовательности тогда и только тогда, когда из этой последовательности можно выделить подпоследовательность, сходящуюся к этой точке.

 — предельная точка последовательности 

Иногда это свойство принимают за определение, а приведённое выше определение — за свойство.

• Всякая сходящаяся числовая последовательность имеет только одну предельную точку.

 — предельные точки последовательности 

• Предельная точка любой сходящейся числовой последовательности совпадает с её пределом.

 — предельная точка последовательности 

• Для любого конечного или счётного множества точек можно построить последовательность, для которой эти точки будут являться предельными и никакие, кроме них.

• У произвольной числовой последовальности имеется хотя бы одна предельная точка (либо вещественная, либо бесконечность).

9. Фундаментальные последовательности и их свойство. Критерий Коши сходимости

числовой последовательности.

Определение

Последовательность точек   метрического пространства   называется фундаментальной, если она удовлетворяет критерию Коши:

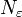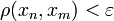для любого   существует такое натуральное  , что   для всех  .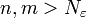

[править]Связанные определения

• Пространство, в котором каждая фундаментальная последовательность сходится к элементу этого же пространства, называется полным.

[править]Доказательство

Пусть   — последовательность, которая сходится к точке  .

Фиксируем  .

Тогда, согласно определению предела последовательности, существует такой номер  , что для всякого  , будет иметь место неравенство  .

Теперь, по неравенству треугольника,   для любых   и  , что и требовалось показать согласно определению (сходимости в себе).

[править]Свойства

• Каждая сходящаяся последовательность является фундаментальной, но не каждая фундаментальная последовательность сходится.

• Метрическое пространство является полным тогда и только тогда, когда всякая система вложенных замкнутых шаров с неограниченно убывающим радиусом имеет непустое пересечение, состоящее из одной точки.

• Если последовательность фундаментальна и содержит сходящуюся подпоследовательность, то сама последовательность сходится.

• Теорема 4.4.1 ( Критерий Коши ) Для того, чтобы последовательность { x_n } сходилась, необходимо и достаточно чтобы она была фундаментальной.  Доказательство. Необходимость. Пусть x_n 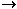  a при n 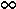   . Тогда для любого     0 существует N (   ), что для любых n, m   N (   ) выполняется | x_n - a |     / 2, | x_m - a |     / 2. Рассмотрим цепочку неравенств

• | x_n - x_m | = | ( x_n - a ) + ( a - x_m ) |   | x_n - a | + | x_m - a |   

• что означает, что { x_n } фундаментальна.  Достаточность. Докажем сначала ограниченность последовательности { x_n }. Возьмем   = 1   0 , тогда по фундаментальности { x_n }, найдется N(   ), что для всех n, m   N (   )выполняется | x_n - x_m |   1. Следовательно, | x_n | - | x_m |   | x_n - x_m |   1, поэтому | x_n |   1 + | x_m | . Итак, для всех n   N (   ) при фиксированном m   N (   ) выполняется | x_n |   1 + | x_m |, что означает ограниченность последовательности  { x_n }, ( см. замечание 3.2.1 ). По теореме 4.3.2 из последовательности { x_n } можно выделить подпослеловательность, сходящуюся к некоторому числу a. Докажем, что и вся последовательность сходится к числу a.  Возьмем любое     0, тогда найдется номер N ( из фундаментальности { x_n } ), что для всех n, m   N выполняется | x_n - x_m |     / 2. В виду сходимости x_nk   a при k     по взятому    0 найдется номер k⁰, такой, что nk0   N и | x_nk0 - a |     / 2 . Тогда для любого n   N

• | x_n - a | = | x_n - x_m + x_m - a | = [ x_m = x_nk0 ]   | x_n - x_m | + | x_nk0 - a |     ,

• что означает сходимость последовательности { x_n } к числу a.

10.. Предел функции. Теорема о связи двустороннего предела с односторонними.