
Определения
Рассмотрим функцию ![]() ,
определённую на некотором множестве
,
определённую на некотором множестве ![]() ,
которое имеет предельную
точку
,
которое имеет предельную
точку ![]() (которая,
в свою очередь, не обязана ему принадлежать).
(которая,
в свою очередь, не обязана ему принадлежать).
[Править]Предел функции по Гейне
Значение ![]() называется пределом (предельным
значением)
функции
в
точке
,
если для любой последовательности точек
называется пределом (предельным
значением)
функции
в
точке
,
если для любой последовательности точек ![]() ,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции ![]() сходится
к
.[1]
сходится
к
.[1]
![]()
[Править]Предел функции по Коши
Значение
называется пределом (предельным
значением)
функции
в
точке
,
если для любого наперёд взятого
положительного числа ![]() найдётся
отвечающее ему положительное число
найдётся
отвечающее ему положительное число ![]() такое,
что для всех аргументов
,
удовлетворяющих условию
такое,
что для всех аргументов
,
удовлетворяющих условию ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .[1]
.[1]
![]()
Пусть f(x) определена в проколотой окрестности точки а, тогда
Lim (x->a) f(x)=b (lim(x-> a+0) f(x)=b) and (lim (x->a-0) f(x)=b).
Доказательство.
Существует lim (x->a) f(x)=b любой эпсилон>0 существует дельта(эпсилон)>0, такое, что любой x принадлежит проколотой окрестности точки а при отрезке дельта, /f(x)-b/<EPS.
0</x-a/<дельта (a-дельта<x<a) or (a<x<a+дельта).
Тогда получим, что x принадлежит проколотой окрестности точки (а+-0) на отрезке дельта =>
/f(x)-b/ <EPS=>существует lim (x->a+-0) f(x)=b.
Дельта1: дельта12(EPS)>0 a<x<a+дельта /f(x)-b/<EPS
Любой EPS, дельта (EPS)=min{дельта1(EPS),дельта2(EPS) }, тогда
Любой x принадлежит проколотой окрестности точки а на отрезке дельта, /f(x)-b/<EPS существует lim(x->a) f(x)=b.
11. Локальная ограниченность функции, имеющей конечный предел
Область
определения D функции f
cодержит некоторую ![]()
f локально ограничена в точке x0, если она ограничена в некоторой окрестности этой точки $M$d>0"xÎU(x0)ÇD:|f(x)|£M.
Т. Функция f имеющая конечный предел в окрестности точки x0 локально ограничена в точке x0.
Доказательство: e=1,M=max{|A-1|,|A+1|,f(x0)} или M=max{|A-1|,|A+1|}
Замечание.
Теорема верна и в случае ![]()
F(x)<M.
/f(x)/=/f(x)-b+b/<=/f(x)-b/+/b/<EPS+/b/=M.
12. Бесконечно малые функции. Теорема о связи функции, ее предела и бесконечно малой.
17.1. Определения и основные теоремы
Функция у=f(х) назівается бесконечно малой при х→x0,если
![]()
По определению предела функции равенство (17.1) означает: для любого числа ε>0 найдется число δ>0 такое, что для всех х, удовлетворяющих неравенству 0<|х-x0|<δ, выполняется неравенство |ƒ(х)|<ε.
Аналогично определяется б.м.ф. при х→хо+0, х→x0-0, х→+∞, х→-∞: во всех этих случаях ƒ(х)→0.
Бесконечно малые функции часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами α, ß и т. д.
Пример:хn=1/n, nєN, — бесконечно малая последовательность.
Теорема 17.5. Если функция ƒ(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции α(х), т. е. если limƒ(х)=А, при Х→Хо то ƒ(х)=А+а(х).
▼ Пусть ![]()
Следовательно,
![]() т.
е. |ƒ(х)-А-0|<ε. Это означает, что функция
ƒ(х)-А имеет предел, равный нулю, т. е.
является б.м.ф., которую обозначим через
α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).▲
т.
е. |ƒ(х)-А-0|<ε. Это означает, что функция
ƒ(х)-А имеет предел, равный нулю, т. е.
является б.м.ф., которую обозначим через
α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).▲
13. Теоремы о сумме бесконечно малых и произведении б.м. на ограниченную функцию.
Теорема 17.2 Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
▼ Пусть функция ƒ(х) ограничена при х→хо. Тогда существует такое число М>0, что
![]() для
всех х из δ1-окрестности
точки хо.
И пусть α(х)—б.м.ф. при х→x0.
Тогда для любого ε >0,
а значит, и ε /М>
0 найдется такое число δ2>О,
что при всех х, удовлетворяющих неравенству
0<|х-хо|<δ2,
выполняется неравенство
для
всех х из δ1-окрестности
точки хо.
И пусть α(х)—б.м.ф. при х→x0.
Тогда для любого ε >0,
а значит, и ε /М>
0 найдется такое число δ2>О,
что при всех х, удовлетворяющих неравенству
0<|х-хо|<δ2,
выполняется неравенство
![]()
Обозначим через δ наименьшее из чисел δ1 и δ2. Тогда для всех х, удовлетворяющих неравенству 0<|х-хо|<δ, выполняются оба неравенства (17.4) и (17.5). Следовательно, |ƒ(х)-α(х)|=|ƒ(х)|-|а(х)|<ε.
А это означает, что произведение ƒ(х)•α(х) при х→х0 есть бесконечно малая функция.▲
Следствие 17.1. Так как всякая б.м.ф. ограничена, то из теоремы (17.2) вытекает: произведение двух б.м.ф. есть функция бесконечно малая.
Следствие 17.2. Произведение б.м.ф. на число есть функция бесконечно малая.
Теорема 2. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство. Пусть ![]() и
и ![]() –
бесконечно малые последовательности.
Это означает, что для любого
числа
–
бесконечно малые последовательности.
Это означает, что для любого
числа ![]() существуют
такие номера
существуют
такие номера ![]() и
и ![]() ,
что для всех номеров
,
что для всех номеров ![]() и
для всех номеров
и
для всех номеров ![]() выполняются
условия
выполняются
условия ![]() и
и ![]() соответственно.
Тогда для всех номеров
соответственно.
Тогда для всех номеров ![]() выполняется
условие
выполняется
условие![]()
![]() ,
а это и означает, что последовательность
,
а это и означает, что последовательность ![]() –
бесконечно малая.
–
бесконечно малая.
Следствие 1. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Следствие 2. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
14. Теорема о пределе суммы, произведения, частного функций.
Т.3:
Предел суммы конечного числа функций,
имеющих пределы при х![]() а,
равен сумме их пределов
а,
равен сумме их пределов
Пусть![]() тогда
по теореме 2 име-
тогда
по теореме 2 име-
ем![]() где
где![]() —
б.м. при
—
б.м. при
х![]() а,
следовательно,
а,
следовательно,![]() Используя
лемму 1 о б.м., заключаем, что
Используя
лемму 1 о б.м., заключаем, что![]() —
б.м. при
—
б.м. при
![]() и
по теореме 2 получаем равенство
и
по теореме 2 получаем равенство![]() b1
+ b2
b1
+ b2
Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:
![]() .
.
Доказательство.
Пусть ![]() .
Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
.
Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Произведение bc есть
величина постоянная. Функция bβ
+ c α + αβ на
основании свойств бесконечно малых
функций есть величина бесконечно малая.
Поэтому ![]() .
.
Следствие 1. Постоянный множитель можно выносить за знак предела:
![]() .
.
Следствие 2. Предел степени равен степени предела:
![]() .
.
Пример.![]() .
.
Т.5:
Предел отношения двух функций, имеющих
пределы при х![]() а,
равен отношению их пределов (если предел
знаменателя не нуль), т.е.
а,
равен отношению их пределов (если предел
знаменателя не нуль), т.е.
![]()
Пусть![]() тогда,
используя Т.2, аналогично доказательству
Т.3 запишем
тогда,
используя Т.2, аналогично доказательству
Т.3 запишем
![]()
где![]() Числитель
последней дроби по леммам о б.м. является
б.м. Покажем, что
Числитель
последней дроби по леммам о б.м. является
б.м. Покажем, что![]() является
функцией ограниченной, тогда дробь по
лемме 2 о б.м. является б.м., и по Т.2:
является
функцией ограниченной, тогда дробь по
лемме 2 о б.м. является б.м., и по Т.2:![]()
Имеем
в некоторой![]() окрестности
т. а для любого
окрестности
т. а для любого![]() >
0 вследствие справедливости
>
0 вследствие справедливости![]()
![]()
т.е.
ограниченность![]() доказана
доказана
15. Теорема о пределе сложной функции.
Теорема 3 (о пределе сложной функции). Если существует конечный предел
![]()
а
функция f(u) непрерывна в точке ![]() ,
то
,
то
![]()
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Пример 8. Найти
![]()
Решение. Теорема о пределе частного здесь неприменима, так как
![]()
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
![]()
где
![]()
корни
квадратного трёхчлена. Теперь, полагая ![]() ,
сократим дробь и, используя следствие
из теоремы 1, вычислим предел данной
функции:
,
сократим дробь и, используя следствие
из теоремы 1, вычислим предел данной
функции:
![]()
16. Теорема о знакопостоянстве функции, имеющей отличный от нуля предел
Если
 ,
то существует окрестность точки а, в
которой
,
то существует окрестность точки а, в
которой
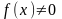 и знак
и знак
 совпадает со знаком значения b.
совпадает со знаком значения b.
Доказательство: по условию
,
т.е.
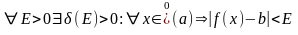 ,
или
,
или
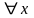 справедливы неравенства
справедливы неравенства
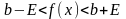 .
.
Возьмём за
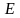 число
число
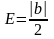 .
Тогда
.
Тогда
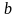 ,
,
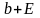 ,
,
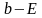 являются числами одного знака.
Следовательно, в силу неравенства
,
и имеет знак числа b в
указанной
являются числами одного знака.
Следовательно, в силу неравенства
,
и имеет знак числа b в
указанной
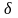 -окрестности
точки а.
-окрестности
точки а.
17. Теорема о предельном переходе в неравенстве.
Теорема 5.1
Если функция имеет предел в некоторой проколотой окрестности точки a, равный A, и принимает неотрицательные значения, то и значение предела этой функции больше или равно 0, т.е.
![]()
![]() ,
,![]()
![]()
Доказательство
(Методом
от противного). Допустим, что A<0.
Возьмем ![]() .
Тогда
.
Тогда ![]()
![]()
![]()
![]() ,
, ![]()
Получаем,
что для любого ![]() из
пересечения проколотых
окрестностей
из
пересечения проколотых
окрестностей ![]() и
и ![]() одновременно
выполняются следующие неравенства:
одновременно
выполняются следующие неравенства:
![]()
![]() и
и![]() .
Тем самым мы пришли к противоречию.
Теорема доказана.
.
Тем самым мы пришли к противоречию.
Теорема доказана.
18. Теорема о пределе промежуточной функции (теорема о 2-х милиционерах)
Теорема 17.10 (о пределе промежуточной функции). Если функция ƒ(х) заключена между двумя функциями φ(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т. е. если
![]()
![]()
то![]()
▼Из равенств (17.6) вытекает, что для любого ε>0 существуют две окрестности δ1 и δ2точки хо, в одной из которых выполняется неравенство |φ(х)-А|<ε, т. е.
-ε<φ(х)-А<ε, (17.8)
а в другой |g(х)-А|<ε, т. е.
-ε<g(х)-А<ε. (17.9)
Пусть δ — меньшее из чисел δ1 и δ2. Тогда в δ-окрестности точки x0 выполняются оба неравенства (17.8) и (17.9). Из неравенств (17.7) находим, что
φ(x)-A≤f(x)-A≤g(x)-A (17.10)
С учетом неравенств (17.8) и (17.9) из неравенства (17.10) следуют неравенства -ε<ƒ(х)-А<ε или |ƒ(х)-А|<ε. Мы доказали, что
ε>0 δ>0 x: 0<|х-х0|<δ |ƒ(х)-А|<ε, то есть lim ƒ(х)=А при х –> x0.
Теорему 17.10 иногда шутливо называют «принципом двух милиционеров». Роль «милиционеров» играют функции φ(х) и g(х), функция ƒ(х) «следует за милиционерами»▲
19. Теорема о связи бесконечно малой и бесконечно большой функции. (лекция №26, тетр. 3)
20. . Первый замечательный предел и следствия из него.
