
- •16. Кратные, криволинейные, поверхностные интегралы.
- •16.1. Двойной интеграл.
- •16.1.3. Свойства двойного интеграла.
- •16.1.5. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •16.1.6. Задачи на двойной интеграл.
- •16.1.7. Приложения двойного интеграла.
- •16.2. Тройной интеграл.
- •16.2.2.3. Интеграл от единичной функции по области V равен объёму этой области: .
- •16.2.5. Замена переменных в тройном интеграле.
- •14.3. Несобственные кратные интегралы.
- •16.3. Криволинейные интегралы.
- •16.3.2. Криволинейный интеграл первого рода (по длине дуги).
- •16.3.2.4. Механические приложения криволинейного интеграла 1-го рода.
- •16.3.3. Криволинейный интеграл второго рода (по координатам).
- •16.3.3.4. Формула Грина.
- •16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.
- •16.4. Поверхностные интегралы.
- •16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
- •16.4.3.3. Вычисление поверхностного интеграла первого рода.
- •6.4.3.4. Механические и физические приложения поверхностного интеграла 1-го рода.
- •16.4. Поверхностные интегралы.
- •16.4.4. Поверхностный интеграл второго рода (по координатам).
- •17. Теория поля.
- •17.1. Скалярное поле.
- •17.1.2. Частные случаи скалярных полей.
- •17.2. Векторное поле.
- •17.2.2. Дифференциальные характеристики векторного поля.
- •17.2.2.1. Дивергенция векторного поля.
- •17.2.3. Частные случаи векторных полей.
- •17.3.Поток векторного поля через поверхность.
16.4. Поверхностные интегралы.
16.4.1. Односторонние и двусторонние поверхности. Ориентация поверхности. Поверхность может быть односторонней и двусторонней. Простой пример модели односторонней поверхности - лист Мёбиуса, который получается, если взять узкую длинную полоску бумаги и склеить её узкие торцы, перекрутив полоску один раз. В том, что у полученной поверхности одна сторона, можно убедиться, если начать закрашивать её в какой-нибудь цвет, не отрывая кисть от бумаги и не пересекая границ. В результате будет окрашен весь лист Мёбиуса. Мы будем рассматривать только двусторонние поверхности.
Поверхность называется гладкой, если в каждой её точке существует касательная плоскость, непрерывно меняющаяся вдоль поверхности. Поверхность называется кусочно-гладкой, если она состоит из нескольких гладких частей, примыкающим друг к другу по гладким или кусочно- гладким кривым. Так, плоскость - гладкая поверхность; поверхность куба - кусочно-гладка.
Д адим
формальное определение односторонней
и двусторонней поверхностей. Пусть дана
гладкая поверхность
адим
формальное определение односторонней
и двусторонней поверхностей. Пусть дана
гладкая поверхность![]() ,
и на ней произвольно выбрана точка М.
Из двух возможных направлений нормали
в этой точке выберем одно и зафиксируем
его. Характеризовать это направление
будем единичным вектором нормали
,
и на ней произвольно выбрана точка М.
Из двух возможных направлений нормали
в этой точке выберем одно и зафиксируем
его. Характеризовать это направление
будем единичным вектором нормали ![]() .
Возьмём замкнутый контур С,
проходящий через точку М,
целиком лежащий в
.
Возьмём замкнутый контур С,
проходящий через точку М,
целиком лежащий в ![]() и не пересекающий её границы, и будем
двигаться по контуру, восстанавливая
в каждой точке нормаль так, чтобы она
непрерывно получалось из
и не пересекающий её границы, и будем
двигаться по контуру, восстанавливая
в каждой точке нормаль так, чтобы она
непрерывно получалось из ![]() .
Если для любого такого контура и любой
точки М мы вернёмся в М с исходным
направлением нормали, то поверхность
.
Если для любого такого контура и любой
точки М мы вернёмся в М с исходным
направлением нормали, то поверхность
![]() называется двусторонней.
Если хотя бы для одного контура мы
вернёмся в исходную точку с противоположным
направлением нормали, то поверхность
называется односторонней.
называется двусторонней.
Если хотя бы для одного контура мы
вернёмся в исходную точку с противоположным
направлением нормали, то поверхность
называется односторонней.
Задать ориентацию
поверхности (выбрать определённую
сторону поверхности)
означает выбрать в каждой точке ![]() один из двух возможных векторов нормали
один из двух возможных векторов нормали
![]() так, чтобы он непрерывно менялся от
точки к точке. Для этого достаточно
определить нормаль
так, чтобы он непрерывно менялся от
точки к точке. Для этого достаточно
определить нормаль ![]() в какой-либо одной точке
в какой-либо одной точке ![]() ;
во всех остальных точках М
направления нормали
;
во всех остальных точках М
направления нормали ![]() должны браться так, чтобы они получались
непрерывным переносом из
должны браться так, чтобы они получались
непрерывным переносом из ![]() вдоль какого-нибудь пути
вдоль какого-нибудь пути ![]() .
Согласно определению двусторонней
поверхности, мы гарантированно придём
в точку
.
Согласно определению двусторонней
поверхности, мы гарантированно придём
в точку ![]() с одним и тем же направлением нормали
при любом пути
с одним и тем же направлением нормали
при любом пути ![]() .
.
1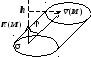 6.4.2.
Поток жидкости через поверхность.Как
и при изучении криволинейных интегралов,
начнём с физической задачи. Пусть через
объём V
течёт поток жидкости, имеющий скорость
6.4.2.
Поток жидкости через поверхность.Как
и при изучении криволинейных интегралов,
начнём с физической задачи. Пусть через
объём V
течёт поток жидкости, имеющий скорость
![]() в
точке М.
Пусть в V
размещена проницаемая (возможно,
воображаемая) поверхность
в
точке М.
Пусть в V
размещена проницаемая (возможно,
воображаемая) поверхность ![]() .
Требуется найти количество
.
Требуется найти количество ![]() жидкости, протекающей через
жидкости, протекающей через ![]() за единицу времени. В дальнейшем мы
будем называть это количество потоком
через поверхность.
за единицу времени. В дальнейшем мы
будем называть это количество потоком
через поверхность.
В случае, когда ![]() - ограниченная плоская область и
- ограниченная плоская область и ![]() ,
решение очевидно. Это количество равно
объёму, ограниченному цилиндрической
поверхностью с основанием
,
решение очевидно. Это количество равно
объёму, ограниченному цилиндрической
поверхностью с основанием ![]() и боковой стороной
и боковой стороной ![]() .
Площадь основания объёма равна
.
Площадь основания объёма равна ![]() (этим символом мы обозначаем и поверхность,
и её площадь), высота
(этим символом мы обозначаем и поверхность,
и её площадь), высота ![]() ,
т.е. равна скалярному произведению
вектора скорости на единичный вектор
нормали. Итак,
,
т.е. равна скалярному произведению
вектора скорости на единичный вектор
нормали. Итак, ![]() .
Заметим, что изобразив на рисунке
единичный вектор нормали, мы ввели на
поверхности ориентацию. Так, применительно
к рисунку справа, мы выбрали верхнюю
сторону поверхности; если бы выбрали
противоположную нормаль, поток изменил
бы знак.
.
Заметим, что изобразив на рисунке
единичный вектор нормали, мы ввели на
поверхности ориентацию. Так, применительно
к рисунку справа, мы выбрали верхнюю
сторону поверхности; если бы выбрали
противоположную нормаль, поток изменил
бы знак.
Возможны два способа представления этой величины.
1. Обозначив ![]() ,
получим
,
получим
![]() .
.
2. Если в некоторой
координатной системе ![]() имеет координаты P,
Q,
R,
единичный вектор
имеет координаты P,
Q,
R,
единичный вектор ![]() имеет координаты - направляющие косинусы
имеет координаты - направляющие косинусы
![]() ,
то
,
то ![]() .
Чему равно произведение
.
Чему равно произведение ![]() ?
Произведение
?
Произведение ![]() равно площади
равно площади ![]() проекции
проекции ![]() поверхности
поверхности ![]() на
на
п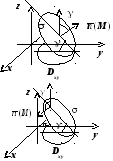 лоскостьOxy
(площади
всегда положительны). Следовательно,
лоскостьOxy
(площади
всегда положительны). Следовательно, ![]() равно
равно ![]() ,
если
,
если ![]() (или, что то же самое, угол
(или, что то же самое, угол ![]() - острый; проекция
- острый; проекция ![]() на орт
на орт ![]() оси Oz
положительна). Этот случай соответствует
верхнему рисунка справа. Соответственно,
оси Oz
положительна). Этот случай соответствует
верхнему рисунка справа. Соответственно,
![]() равно
равно ![]() ,
если
,
если ![]() (или, что то же самое, угол
(или, что то же самое, угол ![]() - тупой; проекция
- тупой; проекция ![]() на орт
на орт ![]() оси Oz
отрицательна). Этот случай соответствует
нижнему рисунку. Итак, можно записать
оси Oz
отрицательна). Этот случай соответствует
нижнему рисунку. Итак, можно записать
![]() .
Аналогично изложенному,
.
Аналогично изложенному, ![]() ,
где следует взять знак "+", если
угол
,
где следует взять знак "+", если
угол ![]() - острый, и "-", если этот угол тупой,
и
- острый, и "-", если этот угол тупой,
и ![]() ,
где берётся знак "+", если угол
,
где берётся знак "+", если угол ![]() - острый, и "-", если этот угол тупой;
- острый, и "-", если этот угол тупой;
![]() - проекция
- проекция ![]() на плоскость Oyz,
на плоскость Oyz,
![]() - - проекция
- - проекция ![]() на плоскость Oxz.
Окончательно,
на плоскость Oxz.
Окончательно, ![]() .
.
Пусть теперь ![]() - произвольная гладкая ограниченная
поверхность, и скорость
- произвольная гладкая ограниченная
поверхность, и скорость ![]() может меняться от точки к точке. Чтобы
свести этот случай к предыдущему,
разобьём
может меняться от точки к точке. Чтобы
свести этот случай к предыдущему,
разобьём ![]() сетью кривых на
сетью кривых на ![]() частей
частей ![]() ,
на каждой из частей
,
на каждой из частей ![]() выберем произвольную точку
выберем произвольную точку ![]() ,
и, считая, что
,
и, считая, что ![]() - плоская область, скорость
- плоская область, скорость ![]() по
по ![]() постоянна и равна
постоянна и равна ![]() и что ориентация всей части
и что ориентация всей части ![]() характеризуется единичным нормальным
вектором
характеризуется единичным нормальным
вектором ![]() ,
получим, что через
,
получим, что через ![]() в единицу времени протекает
в единицу времени протекает ![]() жидкости (
жидкости (![]() ).
Как мы видели, это выражение можно
представить и в виде
).
Как мы видели, это выражение можно
представить и в виде
![]() (где
(где![]()
![]() - угол между
- угол между ![]() и
и ![]() ),
и в виде
),
и в виде ![]() .
Суммируя эти выражения по всем
.
Суммируя эти выражения по всем ![]() дугам, получим выражения двух интегральных
сумм:
дугам, получим выражения двух интегральных
сумм: ![]() и
и ![]() .
Переход к пределу в этих интегральных
суммах при
.
Переход к пределу в этих интегральных
суммах при
![]() приведёт к двум поверхностным интегралам:
приведёт к двум поверхностным интегралам:
![]() и
и ![]() .
Первый из этих интегралов называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности. Во втором интеграле элементы
площади в координатных плоскостям
принято записывать так, как мы это делали
в двойном интеграле:
.
Первый из этих интегралов называется
поверхностным интегралом первого рода,
или поверхностным интегралом по площади
поверхности. Во втором интеграле элементы
площади в координатных плоскостям
принято записывать так, как мы это делали
в двойном интеграле: ![]() и опускать знаки перед слагаемыми:
и опускать знаки перед слагаемыми: ![]() ;
этот интеграл называется поверхностным
интегралом второго рода, или поверхностным
интегралом по координатам. Как и
криволинейные интегралы двух родов,
это разные объекты. Они имеют разные
определения и разные свойства. В
частности, поверхностный интеграл
первого рода не зависит от ориентации
поверхности, так как угол
;
этот интеграл называется поверхностным
интегралом второго рода, или поверхностным
интегралом по координатам. Как и
криволинейные интегралы двух родов,
это разные объекты. Они имеют разные
определения и разные свойства. В
частности, поверхностный интеграл
первого рода не зависит от ориентации
поверхности, так как угол
![]() входит в подынтегральную функцию в
явном виде, в то время как поверхностный
интеграл второго рода меняет знак при
изменении стороны поверхности (вектор
входит в подынтегральную функцию в
явном виде, в то время как поверхностный
интеграл второго рода меняет знак при
изменении стороны поверхности (вектор
![]() меняется на
меняется на ![]() ).
).
Перейдём к формальным определениям.
