
- •16. Кратные, криволинейные, поверхностные интегралы.
- •16.1. Двойной интеграл.
- •16.1.3. Свойства двойного интеграла.
- •16.1.5. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •16.1.6. Задачи на двойной интеграл.
- •16.1.7. Приложения двойного интеграла.
- •16.2. Тройной интеграл.
- •16.2.2.3. Интеграл от единичной функции по области V равен объёму этой области: .
- •16.2.5. Замена переменных в тройном интеграле.
- •14.3. Несобственные кратные интегралы.
- •16.3. Криволинейные интегралы.
- •16.3.2. Криволинейный интеграл первого рода (по длине дуги).
- •16.3.2.4. Механические приложения криволинейного интеграла 1-го рода.
- •16.3.3. Криволинейный интеграл второго рода (по координатам).
- •16.3.3.4. Формула Грина.
- •16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.
- •16.4. Поверхностные интегралы.
- •16.4.3. Поверхностный интеграл первого рода (по площади поверхности).
- •16.4.3.3. Вычисление поверхностного интеграла первого рода.
- •6.4.3.4. Механические и физические приложения поверхностного интеграла 1-го рода.
- •16.4. Поверхностные интегралы.
- •16.4.4. Поверхностный интеграл второго рода (по координатам).
- •17. Теория поля.
- •17.1. Скалярное поле.
- •17.1.2. Частные случаи скалярных полей.
- •17.2. Векторное поле.
- •17.2.2. Дифференциальные характеристики векторного поля.
- •17.2.2.1. Дивергенция векторного поля.
- •17.2.3. Частные случаи векторных полей.
- •17.3.Поток векторного поля через поверхность.
16.3.3.6. Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.
Если выполнены
условия независимости от формы пути,
соединяющего начальную
![]() и конечную
и конечную ![]() точки кривой, то значение интеграла
точки кривой, то значение интеграла
![]() определяется
только точками А
и В.
Поэтому в этом случае для обозначения
интеграла применяется обозначение
определяется
только точками А
и В.
Поэтому в этом случае для обозначения
интеграла применяется обозначение
![]() или
или
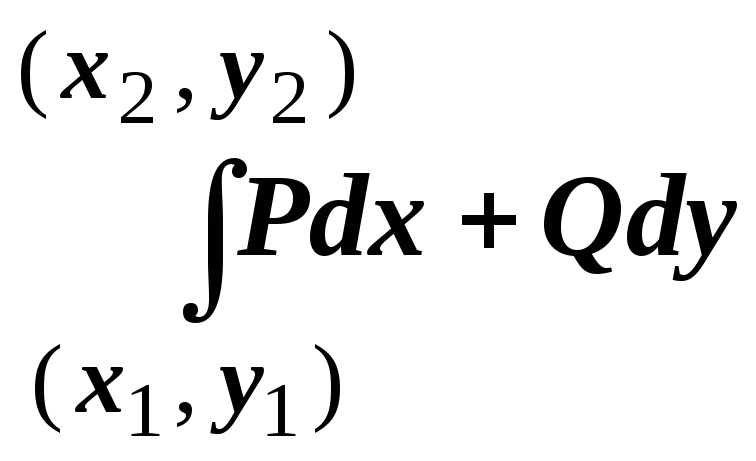 .
Докажем следующую теорему.
.
Докажем следующую теорему.
Т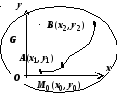 еорема.
Если в односвязной области G
выполнено условие
еорема.
Если в односвязной области G
выполнено условие ![]() ,
то существует функция
,
то существует функция
![]() такая, что для любых точек
такая, что для любых точек
![]() и
и ![]()
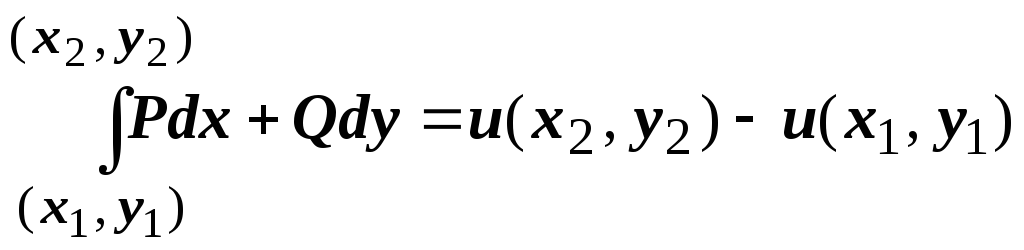 .
.
Функцию
![]() принято называть потенциальной функцией.
принято называть потенциальной функцией.
Доказательство.
Фиксируем
произвольную точку
![]() ,
и докажем, что в качестве искомой функции
,
и докажем, что в качестве искомой функции
![]() можно взять
можно взять
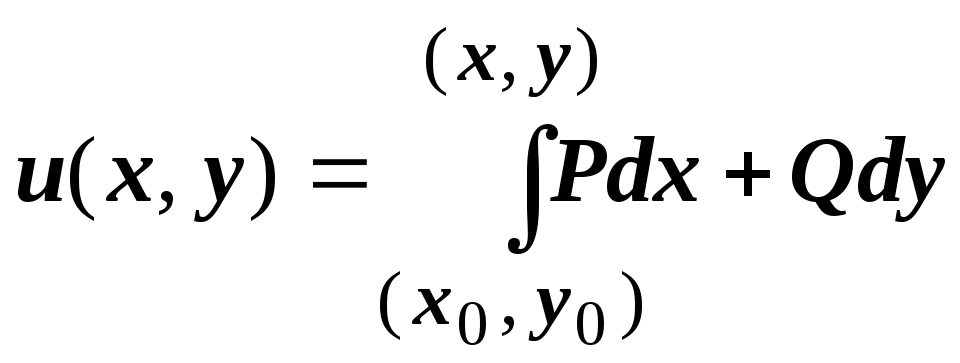 .
Действительно,
по свойству аддитивности
.
Действительно,
по свойству аддитивности
![]()
![]()
![]() ,
или
,
или
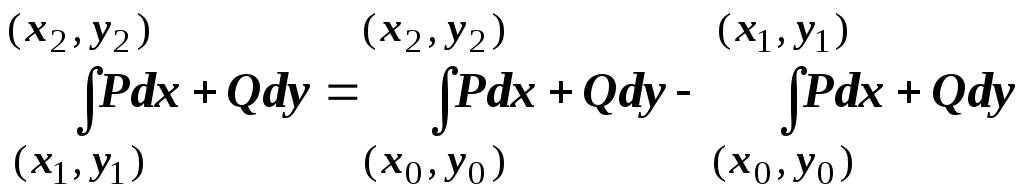 ,
т.е.
,
т.е.
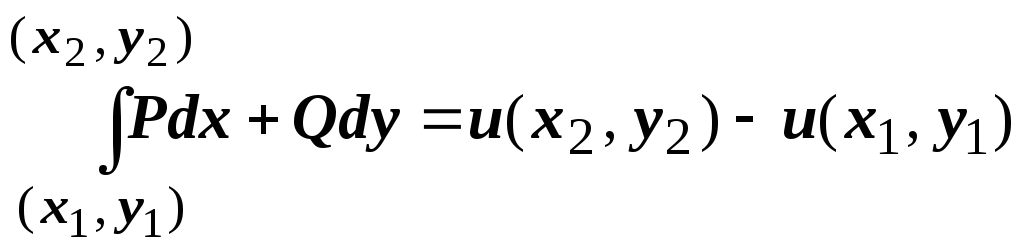 ,
что и требовалось доказать.
,
что и требовалось доказать.
Разность
![]() обозначается
символом
обозначается
символом
![]() или
или
![]() .
Формула
.
Формула
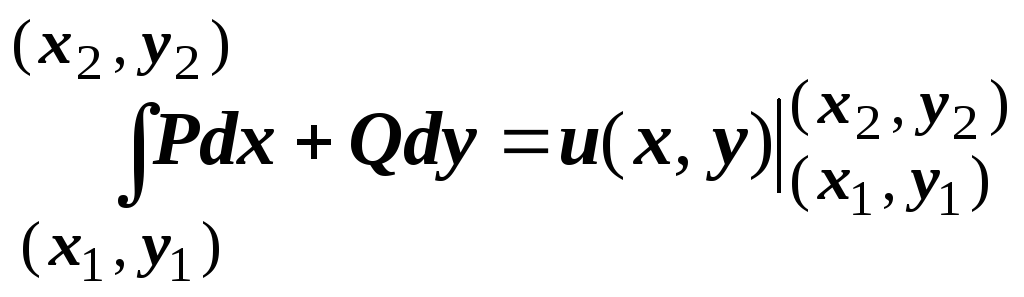 является аналогом формулы Ньютона-Лейбница
для двухмерного случая; ещё раз отметим,
что она имеет место в случае, когда
выполняются условия независимости
интеграла от формы пути.
является аналогом формулы Ньютона-Лейбница
для двухмерного случая; ещё раз отметим,
что она имеет место в случае, когда
выполняются условия независимости
интеграла от формы пути.
Д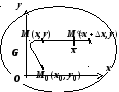 окажем,
что для построенной функции
окажем,
что для построенной функции
![]() выполняются следующие соотношения:
выполняются следующие соотношения:
![]() .
Действительно, пусть
.
Действительно, пусть ![]()
![]() .
Тогда
.
Тогда ![]() ,
,
![]()
![]() (на
(на ![]() )
)
![]()
![]() (по теореме о среднем)
(по теореме о среднем) ![]() .
Точка
.
Точка ![]() удовлетворяет условиям
удовлетворяет условиям ![]() .
Устремим
.
Устремим ![]() ,
тогда
,
тогда ![]() ,
и
,
и ![]() .
.
Аналогично
доказывается, что ![]() .
.
 Условие
Условие![]() теперь означает просто, что
теперь означает просто, что ![]() .
Кроме того, из
.
Кроме того, из ![]()
![]() следует, что подынтегральное выражение
следует, что подынтегральное выражение
![]()
![]() является полным дифференциалом функции
является полным дифференциалом функции
![]() (условие
(условие ![]() есть условие того, что обыкновенное
дифференциальное уравнение первого
порядка
есть условие того, что обыкновенное
дифференциальное уравнение первого
порядка ![]() - уравнение в полных дифференциалах).
Для отыскания потенциальной функции
- уравнение в полных дифференциалах).
Для отыскания потенциальной функции ![]() можно: 1. Решить уравнение в полных
дифференциалах; 2. Построить
можно: 1. Решить уравнение в полных
дифференциалах; 2. Построить ![]() напрямую по формуле
напрямую по формуле
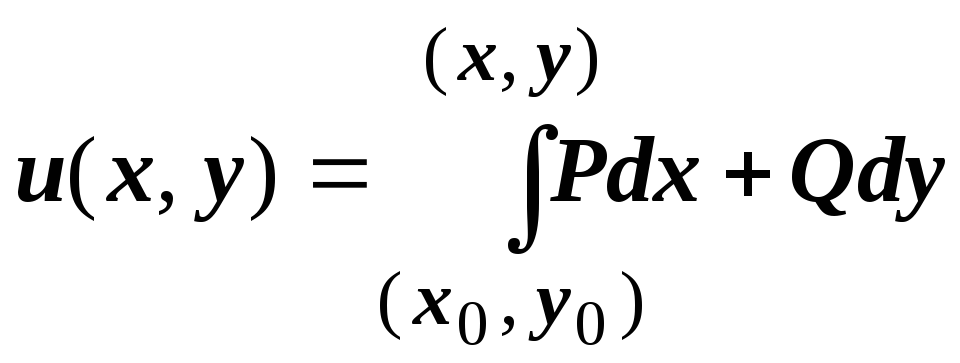 .
В качестве пути интегрирования обычно
берётся путь М0АМ,
состоящий из отрезков, параллельных
координатным осям.
.
В качестве пути интегрирования обычно
берётся путь М0АМ,
состоящий из отрезков, параллельных
координатным осям.
Тогда на М0А
![]()
![]() ;
на АМ
;
на АМ ![]() .
.
Продемонстрируем
оба метода на примере 4 раздела 16.3.3.3:
![]() .
Здесь
.
Здесь ![]()
![]() ,
т.е. условия независимости выполняются.
В качестве точки
,
т.е. условия независимости выполняются.
В качестве точки ![]() берём начало координат
берём начало координат ![]() .
.
Решаем систему уравнений
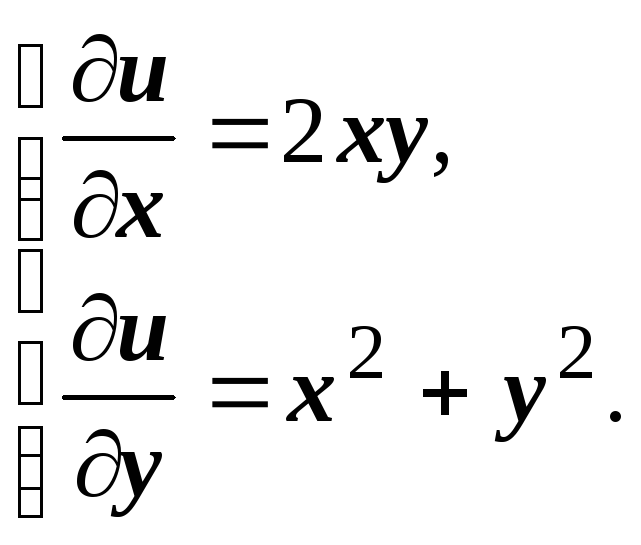 Из первого уравнения
Из первого уравнения 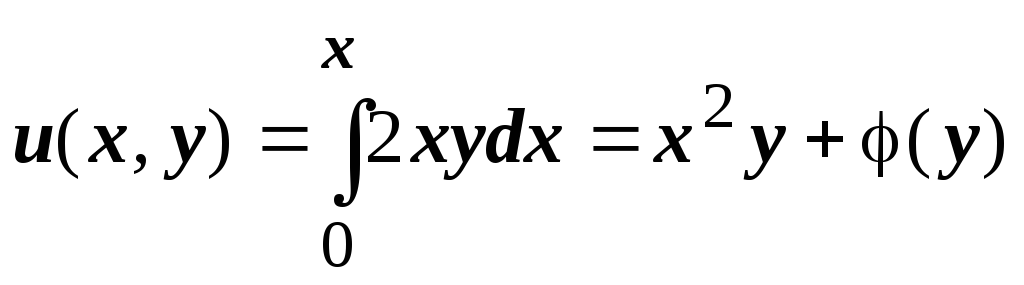 ,
подставляем эту функцию во второе
уравнение
,
подставляем эту функцию во второе
уравнение 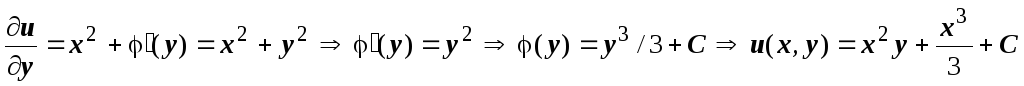 (потенциал всегда определяется с
точностью до произвольной постоянной,
физический смысл имеет разность
потенциалов в двух точках, которая не
зависит от этой постоянной).
(потенциал всегда определяется с
точностью до произвольной постоянной,
физический смысл имеет разность
потенциалов в двух точках, которая не
зависит от этой постоянной).
2.
![]() .
.
Теперь, когда
потенциальная функция определена, легко
находится любой интеграл: 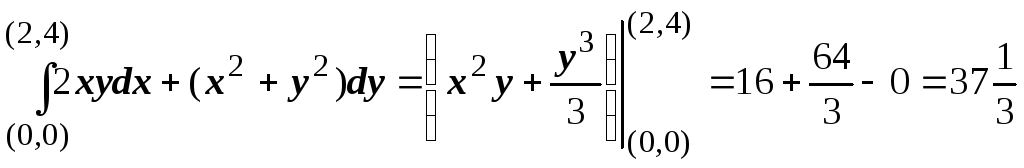 .
.
16.3.3.7. Выражение
площади плоской области через криволинейный
интеграл. Из
формулы Грина ![]() следует неожиданный результат: если
функции Р
и Q
удовлетворяют условию
следует неожиданный результат: если
функции Р
и Q
удовлетворяют условию ![]() ,
то
,
то ![]() (
(![]() - площадь области D).
Таким образом, площадь области можно
выразить через криволинейный интеграл
второго рода по границе этой области.
В качестве функций Р
и Q
можно взять любые непрерывно
дифференцируемые функции, такие что
- площадь области D).
Таким образом, площадь области можно
выразить через криволинейный интеграл
второго рода по границе этой области.
В качестве функций Р
и Q
можно взять любые непрерывно
дифференцируемые функции, такие что ![]() ,
например,
,
например,
![]() ;
;![]() ;
;![]() ;
;![]() и т.д. В результате
и т.д. В результате![]() и т.д. При этом контур С
(граница области D)
обходится в положительном направлении.
Чаще всего применяется третья из этих
формул. Для примера найдём площадь,
ограниченную эллипсом
и т.д. При этом контур С
(граница области D)
обходится в положительном направлении.
Чаще всего применяется третья из этих
формул. Для примера найдём площадь,
ограниченную эллипсом
![]() .
Параметрические уравнения эллипса
.
Параметрические уравнения эллипса![]() ,
поэтому
,
поэтому![]() ;
это, видимо, самый простой способ
вычисления площади эллиптической
области.
;
это, видимо, самый простой способ
вычисления площади эллиптической
области.
