1.2. Операции над множествами.

        В этом параграфе будут рассмотрены три простые операции, которые можно производить над множествами: объединение, пересечение и разность (дополнение) множеств.

        Опр.1.2. Пусть даны множества А и В. Их объединением называется множество С, состоящее из элементов, принадлежащих хотя бы одному из множеств А, В.         Объединение множеств обозначается символами "+" и "∪": C=A∪B. Пусть, например, А={-6, -3, 0, 3, 6}, B={0,2, 4, 6, 8}. Тогда A∪B = {-6, -3, 0, 2, 3, 4, 6, 8}. Геометрически объединение множеств изображено на рис. 2.         Аналогично определяется объединение большего числа множеств.         Опр.1.3. Объединением множеств А₁, А₂, А₃, …, А_n (обозначение ) называется множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А₁, А₂, А₃, …, А_n.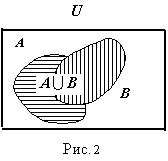

Свойства операции объединения.

        Теор. 1.1. Справедливы следующие равенства:

1. A∪B = B∪A (коммутативность);

2. (А∪B) ∪C = А (B∪C) (ассоциативность);

3. Если A⊇B, то А∪В= А;

4. объединение А и пустого множества равно А.

        Док-во. Формулы, подобные формулам 1-2, обычно доказываются так. Берётся элемент, принадлежащий правой части равенства, и доказывается, что он принадлежит левой части. В результате для формулы 1, например, будет доказано, что A∪B ⊆ B∪A. Затем берётся элемент, принадлежащий левой части, и доказывается, что он принадлежит правой части равенства; для формулы 1 это будет означать, что B∪A ⊆ A∪B. Из включений A∪B ⊆ B∪A и B∪A ⊆ A∪B следует, что A∪B = B∪A.         Итак, пусть a ∈ А∪В. Это значит, что либо a ∈ А, либо a ∈ B, либо эти включения имеют место одновременно. Во всех трех случаях a ∈ B∪A. Включение A∪B ⊆ B∪A доказано. Пусть теперь a ∈ B∪A. Это значит, что либо a ∈ B, либо a ∈ A, либо эти включения имеют место одновременно. Во всех трех случаях a ∈ A∪B. Включение B∪A ⊆ A∪B доказано. Следовательно, A∪B = B∪A, что и требовалось доказать.         Другой способ доказательства - изобразить левую и правую часть равенства для одних и тех же множеств на диаграммах Эйлера-Венна и убедиться, что они изображают одно и тоже множество. Так, для формулы 1 диаграммы приведены на рисунке слева.         Задание. Самостоятельно доказать включения соответствующих множеств и изобразить диаграммы для формул 2-4.

        Опр.1.4. Пересечением множеств А и В называется множество С, состоящее из элементов, принадлежащих одновременно и множеству А, и множеству В. Если множества А и Вне имеют общих элементов, их пересечение равно пустому множеству; в этом случае множества А и В называются непересекающимися.         Пересечение множеств обозначается символами "∩" и "·" (знак умножения): С = А∩В или С = АВ. Для примера, приведенного после опр.1.2, А∩В = {0, 6}. Геометрически пересечение множеств представлено на рис. 3.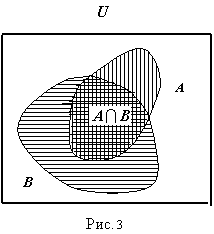

Свойства операции пересечения множеств.

        Теор. 1.2. Справедливы следующие равенства:

1. A∩B = B∩A (коммутативность);

2. (A∩В)∩С = А∩(В∩С) (ассоциативность);

3. Если A⊇B, то А∩B = В;

4. А∩= .

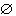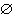        Задание. Самостоятельно доказать включения соответствующих множеств и изобразить диаграммы для формул 5-8.         Опр. 1.5 пересечения множеств для большего числа множеств: Пересечением множеств А₁, А₂, А₃, …, А_n ( обозначение ) называется множество, состоящее из элементов, входящих в каждое из множеств А₁, А₂, А ₃, …, А_n.         Теор. 1.3. Для операций объединения и пересечения множеств справедливы законы дистрибутивности:

1. A∪(B∩C) = (A∪B)∩(A∪C);

2. A∩(B∪C) = (A∩B)∪(A∩C);.

        Док-во: Докажем формулу 9. Пусть a ∈ A∪(B∩C). Тогда либо a ∈ A (следовательно, a ∈ A∪B и a ∈ A∪C, т.е. a ∈ (A∪B)∩(A∪C); либо a ∈ B∩C (следовательно, одновременно, a ∈ B и a ∈ C ⇒ a ∈ A∪B и a ∈ A ∪ C, т.е. a ∈ (A∪B)∩(A∪C); либо одновременно a ∈ A и a ∈ C (в этом случае можно применить любое из приведённых выше рассуждений). Таким образом, доказано, что A∪(B∩C) ⊆ (A∪B)∩(A∪C).         Пусть a ∈ (A∪B)∩(A∪C). Рассмотрим два случая. 1. Пусть a ∈ A. Тогда a ∈ A∪(B∩C). 2. Пусть aA , но a ∈ (A∪B)∩(A∪C), т.е. одновременно и a ∈ A∪B, и a ∈ A∪C. Это возможно, только если одновременно a ∈ B и a ∈ C; т.е. a ∈ B∩C, откуда следует, что a ∈ A∪(B∩C). Включение (A∪B)∩(A∪C) ⊆ A∪(B∩C) доказано.         Задание. Самостоятельно доказать формулу 10.

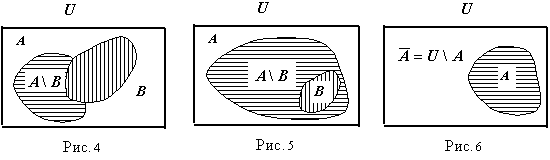
        Опр. 1.6. Разностью множеств А и В называется множество А\В, содержащее те элементы множества А, которые не принадлежат множеству В.         В опр. 1.6 не предполагается, что В ⊆ A (рис. 4). Если же В ⊆ A, то разность А\В называется дополнением множества В до множества А (рис. 5). Для дополнения множества А до универсального множества U применяется обозначение (рис. 6).

        Теор. 1.4. Операции разности и дополнения антидистрибутивны относительно операций объединения и пересечения:

11. A\(B∪C) = (A\B)∩(A\C);

12. A\(B∩C) = (A\B)∪(A\C).

        (Дополнение к объединению некоторых множеств равно пересечению их дополнений; дополнение к пересечению множеств равно объединению их дополнений.)         Док-во. Докажем формулу 11. Пусть a ∈ A\(B∪C). Это означает, что a ∈ A и aB∪C, т.е. aB, aC. Следовательно, a ∈ A\B и a ∈ A\C, т.е. a ∈ (A\B)∩(A\C). Включение A\(B∪C) ⊆ (A\B)∩(A\C) доказано.         Пусть a ∈ (A\B)∩(A\C). Это означает, что одновременно a ∈ A\B (т.е. a ∈ A и aB), и a ∈ A\C (т.е. a ∈ A и aC). Так как aB и aC, то aB∪C. Но a ∈ A, следовательно, a ∈ A\(B∪C). Включение (A\B)∩(A\C) ⊆ A\(B∪C) доказано. Из справедливости доказанных включений следует справедливость формулы 11.

        Задание. Самостоятельно доказать формулу 12 и обобщение формул 11, 12 на большее число множеств:

        13. 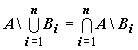;         14. .

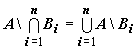.3. Мощность множества.

        Количество элементов в конечном множестве естественно характеризовать их числом. В этом смысле множество чисел {-2, 0, 3,8} и множество букв {с, х, ф, а} эквивалентны, так как они содержат одинаковое число элементов. Для бесконечных множеств такого простого правила сравнения количеств элементов в них нет; чтобы получить возможность описывать количество элементов в бесконечных множествах, введём следующие определения.

        Опр. 1.7. Между множествами Аи В установлено взаимно-однозначное соответствие, если каждому элементу множества А каким-либо образом сопоставлен единственный элемент множества В, при этом каждому элементу множества В сопоставляетсяединственный элемент множества А.         Опр. 1.8. Множества, между которыми можно установить взаимно-однозначное соответствие, называются равномощными (имеющими одинаковую мощность, эквивалентными). Равномощность множеств обозначается символом "~": А ~ В.         Так, для приведённых выше множеств.взаимно-однозначное соответствие устанавливается соотношениями -2 ↔ с, 0 ↔ ф, 3 ↔ а, 8 ↔ х. Однако ценность опр. 1.8 эквивалентности множеств заключается в том, что оно применимо к любым, в том числе бесконечным, множествам. Так, рассмотрим множество N натуральных чисел и множество N2 = {2, 4, 6, …} четных чисел. Взаимно-однозначное соответствие между этими множествами устанавливается соотношениями n ↔ 2n, следовательно, эти множества равномощны: N ~ N2. Этот пример показывает, что собственное подмножество может быть равномощным всему множеству; естественно, это может быть только для бесконечных множеств.         Соотношение ~ эквивалентности множеств транзитивно: если А ~ В, В ~ С, то А ~ С. Взаимно-однозначное соответствие между элементами а и с множеств А и С устанавливается по цепочке а ↔ в ↔ с.

        Опр. 1.9. Множество, эквивалентное множеству натуральных чисел N называется счётным множеством.         Другими словами, множество счётно, если его элементы можно перенумеровать всеми натуральными числами. Счётны множества N2 чётных натуральных чисел, множество нечётных чисел (соответствие n ↔ 2n-1, множество всех целых чисел {0, ±1, ±2, ±3, ±4,…} (соответствие 1 ↔ 0, 2 ↔ -1, 3 ↔ 1, 4 ↔ -2, 5 ↔ 2, …; вообще n ↔ (n-1)/2 для нечётных n и n ↔ -n/2 для чётных n).         Равномощны множества точек любых двух отрезков [a,b] и [c,d] (соответствие можно установить, например, с помощью центрального проектирования; рис. 7). Так же можно доказать равномощность множеств точек любых двух интервалов. 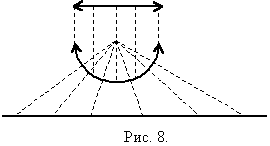Множество точек интервала равномощно множеству точек всей прямой (рис. 8). Сложнее ответить на вопрос, равномощны ли множества точек отрезка и интервала. Положительный ответ на этот вопрос даёт следующая теорема:         Теор. 1.5. Если множество А равномощно подмножеству В₁ множества В, а множество В равномощно подмножеству А₁ множества А, то множества А и В равномощны.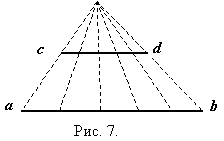

        Опр. 1.10. Множество, эквивалентное множеству точек любого отрезка, называется множеством мощности континуум.         Рассмотрим более подробно свойства счётных множеств и множеств мощности континуум.