2.3.2. Достаточность и необходимость, существование и единственность.
Переведём
формулировку теоремы ∀x∈X
(A(x)
⇒
B(x))
на термины "необходимо", "достаточно":
если для элемента х
множества Х
истинно утверждение А(х),
то истинно и утверждение В(х).
Таким образом, свойство В(х)
необходимо для выполнения А(х)
(если ложно В(х),
то не может быть истинно А(х);
необходимо целое число делится на 5 без
остатка, если его десятичная запись
оканчивается нулём). С другой стороны,
условие А(х)
достаточно для того, чтобы имело место
В(х)
(равенство последней цифры десятичной
записи целого числа нулю достаточно,
чтобы это число делилось на 5 без остатка).
В математике
часто встречаются теоремы, для которых
утверждения А(х)
и В(х)
имеют совпадающие области истинности
и эквивалентны на этих областях: ∀х
∈
Х
(А(х)
⇔
В(х)
("для истинности А(х)
необходима и достаточна истинность
B(х)";
"А(х)
истинно тогда и только тогда, когда
истиино B(х)").
Как следует из формулы 12. (А
⇔
В)
⇔
(А
⇒
В)∧(В
⇒
А)
таблицы "Свойства логических операций",
в этом случае одновременно должны быть
справедливы и прямая, и обратная теоремы
("треугольник прямоугольный тогда и
только тогда, когда квадрат какой-либо
стороны равен сумме квадратов остальных
сторон"). Закономерен вопрос: зачем
вводить два свойства (термина, определения)
для описания одной и той же сущности?
Ответ заключён в приведённом примере:
каждое из свойств может лучше описывать
ту или иную сторону этой сущности (одно
свойство относится к углам, другое - к
сторонам).
Особый
класс математических теорем образуют
теоремы существования. Их структура -
∃х
∈
Х
А(х)
(на множестве Х
существует элемент х,
для которого верно утверждение А(х)).
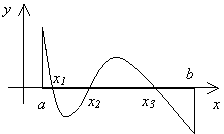
Пример: если непрерывная на отрезке
[a,b]
функция f(x)
принимает на концах отрезка значения
разных знаков, то на [a,b]
существует (хотя бы один) корень уравнения
f(x)
= 0 (приведённая на иллюстрации справа
функция имеет три корня). В некоторых
случаях принципиальна единственность
такого элемента х.
Так, при численном решении уравнения
f(x)
= 0 многие итерационные процессы перестают
работать, если на [a,b]
имеется более чем один корень уравнения.
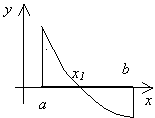
Существование единственного корня
обеспечит такая формулировка теоремы:
"если непрерывная на отрезке [a,b]
функция f(x)
монотонна и принимает на концах отрезка
значения разных знаков, то на [a,b]
существует единственный корень уравнения
f(x)
= 0".
Структура
теорем существования и единственности:
∃!х
∈
Х
А(х).
2.3.3. Доказательство от противного; метод математической индукции .
Здесь
мы рассмотрит два часто применяющихся
метода доказательства теорем:
доказательство от противного и метод
математической индукции.
2.3.3.1.
Доказательство от противного
основано на доказанной нами эквивалентности
(А
⇒
В)
⇔
(
В
⇒
А)
(эквивалентны теоремы прямая и
противоположная обратной). Пример -
известное доказательство того факта,
что
не
может быть рациональным числом
(предположим, что
=
p/q,
где p/q
- несократимая дробь ⇒
p2
= 2q2
⇒
p
- чётно, p
= 2m
⇒
4m2
= 2q2
⇒
q2
= 2m2
⇒
q
- чётно - противоречие с предположением
о несократимости дроби). Таким образом,
для доказательства ∀х∈Х
(А(х)
⇒
В(х))
мы предполагаем, что истинно утверждение
В,
доказываем ∀х∈Х
(
B(х)
⇒
A(х)),
и противоречие между А(х)
и
А(х)
приводит к выводу
В
= В.
2.3.3.2.
Метод математической индукции
часто применяется, если Х
= N
(или Х
- бесконечное подмножество множества
N).
Доказательство утверждения ∀n
∈
N
(А(n)
⇒
В(n))
проводится в два этапа: 1. Доказывается
утверждение А(1);
2. Доказывается ∀n
≥ 1 (А(n)
⇒
А(n+1)).
Рассмотрим простой пример: доказать,
что для любого натурального числа n
сумма квадратов целых чисел от 1 до n
равна n(n+1)(2n+1)/6:
.
При n
=1 равенство справедливо:
.
Пусть
равенство справедливо для n,
докажем что оно справедливо для n+1:
